Copyright © 2000-2015 LHERBAUDIERE	5 pages à l'impression			version initiale 2002
	AVERTISSEMENT				dernière mise à jour 18 mars 2013

PHYSIQUE DU SOLIDE

partie 3/7 : les bandes d'énergie

bandes d'énergie			comment les remplir
travail de sortie			l'électron peut-il quitter le solide?
				une collection d'icônes pour visiter tout le site

En pratique la structure cristalline se traduit par la mise en commun de ces électrons périphériques qui vont alors disposer d'une beaucoup plus grande liberté d'action.

On rencontrera donc deux types d'électrons :

• ceux pour lesquels les interactions des autres noyaux sont si fortes qu'ils sont pratiquement libérés de leur atome initial et circulent de proche en proche dans l'ensemble du solide sous l'effet des champs électromagnétiques générés par les autres particules chargées du solide.
• et ceux qui sont plus proches d'un noyau donné auquel ils restent liés malgré la perturbation de leur état énergétique par les actions des autres noyaux.

Pour satisfaire le principe de Pauli on constate qu'il y a une véritable démultiplication des niveaux énergétiques de l'atome isolé et dans un cristal (assemblage régulier d'atomes) ce phénomène se traduit par l'existence de quasi "bandes d'énergie" dont la représentation conventionnelle nous aidera à expliquer bien des propriétés du semiconducteur et les applications pratiques en découlant. Notons que deux bandes d'énergie permises sont séparées par une bande dite interdite de largeur plus ou moins importante, et que parfois deux bandes permises se chevauchent en ne formant alors qu'une unique bande permise plus large caractérisant des matériaux différents, semiconducteur ou isolant dans le premier cas, métal conducteur dans le dernier.

3 Bandes d'énergie

L'un des éléments importants est la compréhension des mécanismes de remplissage de ces bandes d'énergie. Un assemblage de N atomes de Z électrons va donc disposer de NZ cases réparties en plusieurs bandes d'énergie, mais les nombres quantiques peuvent prendre une infinité de valeurs ce qui signifie que le nombre de cases possibles est lui-même infini. Comment se fait la répartition entre les niveaux véritablement occupés?

Plaçons nous tout d'abord au zéro absolu, c'est à dire dans les conditions énergétiques minimales. Le bon sens nous indique que ce sont les cases quantiques de moindre énergie qui seront occupées et qu'il y aura nécessairement une case au delà de laquelle toutes les cases seront vides, et en deça de laquelle toutes seront occupées par 2 électrons de spins opposés. Ce niveau limite est dit niveau de Fermi.

Notons que deux cas sont possibles : Soit ce niveau se trouve à l'intérieur d'une bande d'énergie et au dessus de ce niveau la bande est vide, ce sera le cas des métaux. Soit, au zéro absolu, la dernière bande contenant des électrons sera totalement remplie et bien entendu celle immédiatement supérieure sera complètement vide et ce sera le cas des semi-conducteurs. Dans ce dernier cas on démontre que le niveau, dit de Fermi, se trouve (au zéro absolu) au milieu de la bande interdite immédiatement supérieure à la dernière bande remplie.

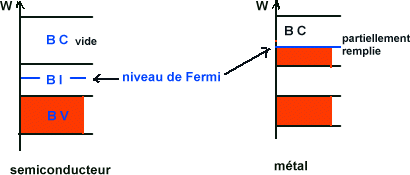
différence entre métal et semiconducteur au zéro absolu

A toute température autre, c'est à dire supérieure au zéro absolu, par hypothèse l'état énergétique est supérieur ce qui implique qu'un certain nombre de cases inférieures au niveau de Fermi seront libres tandis qu'un nombre équivalent à des niveaux supérieurs seront occupées puisque le nombre d'électrons reste évidemment le même. Il est assez intuitif de penser que ce sont principalement les électrons au voisinage du niveau de Fermi (donc les plus périphériques) qui vont voir leur état énergétique croître.

La mécanique quantique nous permet d'apprécier la densité des niveaux occupables possibles en fonction de l'énergie D_e(E) et tout particulièrement au voisinage des limites inférieures (telle E_c pour la bande dite de conduction) et supérieures (telle E_v pour la bande dite de valence) des bandes d'énergie

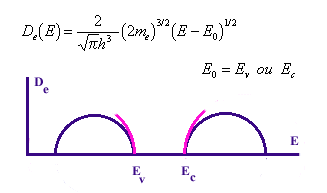
expression de la densité des niveaux permis au voisinage des limites de bandes permise

Pour connaitre le remplissage des niveaux il nous faut une autre information et ce sont les physiciens Fermi et Dirac qui vont nous aider en nous fournissant la probabilité d'occupation d'un niveau d'énergie en fonction de l'énergie de ce niveau et de la température.

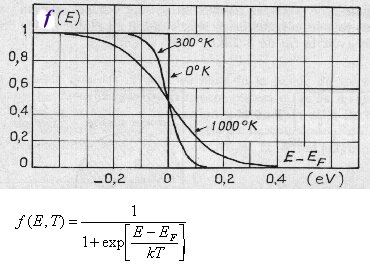
Fig. Fonction de Fermi-Dirac

On peut alors calculer le nombre d'électrons présents dans une tranche d'énergie entre E et E+dE qui s'exprime par

dn = 2 f(E,T) D_e(E) dE

ce qui intégré entre E_c et l'infini permet de déterminer la concentration n d'électrons dans une bande de conduction supposée s'étendre jusqu'à l'infini. Mais, ainsi que le montre la figure ci-dessous, dans la bande dite de conduction Bc les niveaux effectivement occupés sont en nombre très vite voisin de zéro dès qu'on s'éloigne un peu du bas de la bande de conduction. Notons que la surface correspondant aux niveaux occupés dans la bande de conduction est équivalente à celle correspondant aux niveaux vides de la bande de valence. Une avant dernière remarque, dans un semiconducteur pur (intrinsèque) le niveau de Fermi se trouve sensiblement au milieu de la bande interdite.

Fig. représentation des niveaux occupés et vides dans un semiconducteur

On remarque aussi que, dès lors que la température augmente, le nombre de niveaux occupés dans la bande de conduction augmente (en raison de l'évolution de la fonction de répartition) ce qui revient à dire que des électrons sont passés de la bande de valence à celle de conduction et donc que la conductibilité du semiconducteur s'est améliorée.

Le cas du métal est sensiblement différent. Ainsi, dans un métal le nombre d'électrons de conduction (souvent 1 par atome) est invariant en fonction de la température (seul leur niveau énergétique moyen varie selon la loi de Fermi-Dirac, mais ils ne changent pas de bande d'énergie et restent dans la bande de conduction qui est déjà partiellement remplie au zéro absolu) et, au contraire du cas précédent, la conduction se détériore avec un acroissement de la température. En effet quand la température augmente l'oscillation des noyaux autour de leur position d'équilibre augmente freinant le déplacement des électrons libres. Pour comprendre ce "freinage" nous nous rappellerons, tout d'abord, que la matière est constituée d'une immensité de vide ponctuée régulièrement de noyaux chargés positivement, d'électrons liés et d'électrons quasi libres. Ce sont ces derniers qui sont concernés par les phénomènes de transport. Lorsqu'un électron voit son niveau énergétique augmenter cela revient à dire qu'il se déplace plus vite, mais comme il est en permanence soumis à un champ électrique non uniforme il va accélérer et donc voir sa vitesse croître encore plus, mais simultanément augmente aussi sa probabilité de rencontre (collision) avec une autre charge mobile (que ce soit un autre électron ou un noyau), choc qui induit un arrêt ou pour le moins un changement de direction et donc une limitation (diminution) de son parcours moyen entre deux chocs.

Mais les ordres de grandeur sont très différents: ainsi dans le cuivre on a un électron de conduction par atome, tandis que dans le silicium à 25°C on en a seulement 1 pour environ 2000 atomes.

Les propriétés de transport des électrons sont analysées théoriquement en détail dans le chapitre chap_pe1.htm du module consacré aux propriétés des couches minces.

4 travail de sortie

Si au coeur d'un matériau les charges positives (noyaux) sont statistiquement en équilibre avec les négatives (électrons liés et quasi-libres) pour respecter la neutralité, il n'en va pas de même au voisinage des surfaces. Quelques électrons libres ayant une certaine énergie cinétique se dirigent vers la surface et sortent du cristal. Il en résulte un défaut de charge négative sous la surface et, évidemment, une charge négative au delà de la surface donc une charge d'espace r(x) positive dans le cristal et négative dans le vide. Il lui correspond un champ électrique dirigé du métal vers le vide et une ddp telle que le métal est positif par rapport au vide

...
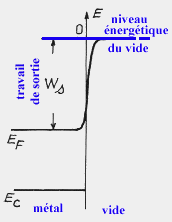
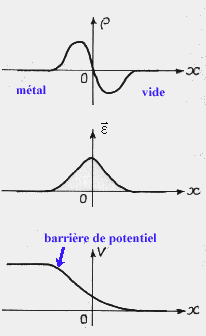
évolution de , et V au voisinage de la surface (x=0) et diagramme énergétique métal-vide

Si on choisit comme origine des potentiels le vide assez loin de la surface, on voit qu'il existe sur la surface du cristal une barrière de potentiel qui empêche les électrons (de charge négative) de quitter le matériau. On peut tracer le diagramme énergétique des électrons dans le système métal-vide. La distance entre E_F niveau le plus élevé rempli à 0K dans le métal et le niveau énergétique du vide W_s représente à 0K le minimum d'énergie à fournir à un électron pour qu'il quitte le matériau. On l'appelle le travail de sortie. Cette barrière de potentiel est spécifiquement un phénomène de surface, ce qui revient à dire que la moindre impureté superficielle (ou pollution) va modifier localement W_s.

Tableau. quelques valeurs expérimentales du travail de sortie