
Copyright
© 2000-2015LHERBAUDIERE
10 pages à l'impression

18 mars 2013
 |
Copyright |
10 pages à l'impression |
 |
version initiale 2003 | |
| dernière
mise à jour 18 mars 2013 |
| rappels de physique du solide | pourquoi parler de ça ici | |||
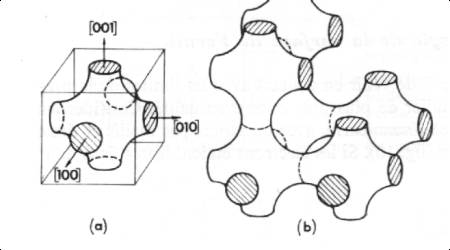
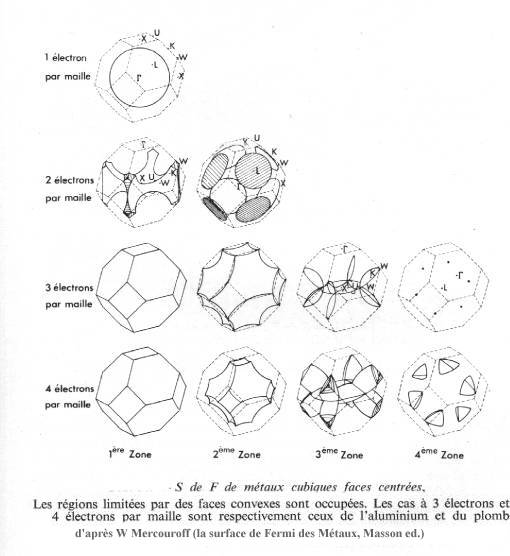
| occupation des niveaux | la surface de Fermi | |||
| résistivité | ||||
| équation de Boltzmann | la base de toute compréhension | |||
| pouvoir thermoélectrique | un phénomène particulier | |||
| une collection d'icônes pour visiter tout le site | ||||
L'un des paramètres essentiels d'un matériau est le libre parcours moyen des électrons (noté lpm ou lm) qui caractérise la distance moyenne franchie par un électron entre deux chocs successifs. Le lpm est spécifique d'un matériau (et de son état structural) et varie en raison inverse de la température. A l'état massif, l'une des causes principales de perturbation est la présence d'impuretés ou de défauts du réseau et tout particulièrement de joints de grain. Les surfaces limites du matériau ont aussi un rôle perturbateur mais celui-ci est généralement limité dans un matériau massif. A l'inverse dans un matériau à l'état de couche mince l'effet perturbateur des surfaces limites va être exacerbé puisque le matériau est dans un état presque bidimensionnel.Pour expliciter les applications, il est bon de voir les spécificités induites dans les propriétés électriques par l'état de couche mince. Les principales propriétés de transport (résistivité, pouvoir thermoélectrique, effet Hall) résultent du déplacement des électrons sous l'effet d'un champ électrique, thermique ou magnétique et de la perturbation de ce déplacement par suite de nombreux chocs soit avec d'autres électrons, soit avec les ions du réseau.
rappels de physique du solide
 on aura de même
on aura de même  =
=  i
+
i
+  r
r =(1/
=(1/ )(d
)(d /d
/d )
) diminue quand
la température
diminue quand
la température  augmente, tandis que
c'est l'inverse pour le second facteur et le coefficient
augmente, tandis que
c'est l'inverse pour le second facteur et le coefficient  va donc varier assez peu (et même parfois pas du tout) sur une assez large
plage de température, plage qui dépend évidemment du métal
considéré. En outre la valeur numérique de ce coefficient
est relativement peu variable d'un métal à un autre puisqu'elle
se situe autour de 4.10-3/°C. La raison en est que les atomes
ont sensiblement les mêmes dimensions d'un métal à un autre
et qu'en conséquence les fluctuations des oscillations des noyaux avec
la température responsables des deux facteurs du coefficient
va donc varier assez peu (et même parfois pas du tout) sur une assez large
plage de température, plage qui dépend évidemment du métal
considéré. En outre la valeur numérique de ce coefficient
est relativement peu variable d'un métal à un autre puisqu'elle
se situe autour de 4.10-3/°C. La raison en est que les atomes
ont sensiblement les mêmes dimensions d'un métal à un autre
et qu'en conséquence les fluctuations des oscillations des noyaux avec
la température responsables des deux facteurs du coefficient  seront proches d'un métal à un autre.
seront proches d'un métal à un autre.| note
1 : On rappelle qu'en mécanique ondulatoire à chaque électron,
d'énergie W et de masse m, est associée une onde
de vecteur d'onde K tel que |
df/dt = df/dx dx/dt + ...+ df/dvx dvx/dt + ...+df/dt dt/dt
(df)champ = df/dx dx + df/dy dy + df/dz dz (changement de position) + df/dvx dvx + df/dvy dvy + df/dvz dvz (variation de vitesse) + df/dt dt (facteur temps)
En divisant terme à terme par dt il vient
 en partant du principe que si la cause de la perturbation cesse alors le système
retourne en un certain temps à son état antérieur. Or ce
retour résulte de la variation par unité de temps du nombre de
collisions, ce que l'on va donc exprimer de la façon suivante:
en partant du principe que si la cause de la perturbation cesse alors le système
retourne en un certain temps à son état antérieur. Or ce
retour résulte de la variation par unité de temps du nombre de
collisions, ce que l'on va donc exprimer de la façon suivante:
 = (
= ( f/
f/ vx)
eEx/m
vx)
eEx/m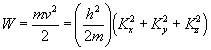
 x
pouvant s'exprimer en fonction de W de même que K, cette expression
se ramène finalement à
x
pouvant s'exprimer en fonction de W de même que K, cette expression
se ramène finalement à et vaut ne2
tF /m
et vaut ne2
tF /m F le temps de relaxation, c'est
à dire la durée moyenne d'un parcours entre deux chocs.
F le temps de relaxation, c'est
à dire la durée moyenne d'un parcours entre deux chocs. le pouvoir thermoélectrique du matériau à la température
considérée
le pouvoir thermoélectrique du matériau à la température
considérée 
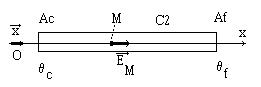
c'est ce qu'on appelle communément l'effet Seebeck.
Considérons tout d'abord un conducteur uniforme supposé en équilibre dans un environnement à température constante, et imaginons que nous examinons ce qui se produit au niveau d'une section unitaire dans le plan perpendiculaire à l'axe du conducteur.
En raison du fait que l'effet Seebeck est particulièrement mal traité dans les manuels de physique, même les plus prestigieux, nous avons choisi d'expliciter très longuement cet effet, d'abord d'une manière phénoménologique accessible au plus grand nombre et ensuite mathématiquement ce qui requièrt une certaine habitude de la mécanique quantique
 c-
c- f.
f.
 est appelé pouvoir thermoélectrique absolu du matériau
ou encore coefficient de Seebeck. L'expérience montre qu'il varie très
légèrement avec la température, mais suffisamment peu pour
qu'on le considère comme approximativement constant sur une certaine
plage de température. Selon l'effet qui sera prépondérant
dans la variation des deux flux d'électrons ce coefficient sera donc
positif ou négatif.
est appelé pouvoir thermoélectrique absolu du matériau
ou encore coefficient de Seebeck. L'expérience montre qu'il varie très
légèrement avec la température, mais suffisamment peu pour
qu'on le considère comme approximativement constant sur une certaine
plage de température. Selon l'effet qui sera prépondérant
dans la variation des deux flux d'électrons ce coefficient sera donc
positif ou négatif.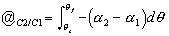
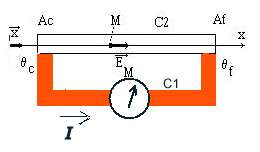
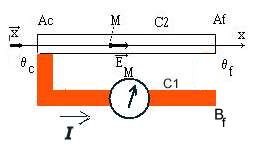
Attention si l'on a, par exemple, choisi des matériaux générant des ddp de signe opposé, qui vont donc s'ajouter, compte tenu de la configuration du circuit, en circuit ouvert et donnant VAf - VBf = @C2- @C1, lorsqu'on ferme le circuit, le courant qui va alors circuler va donc forcément modifier les choses car alors VAc - VAf devra obligatoirement être égal à VAc - VBf puisque Af et Bf sont alors confondus.
Ce qui revient à @C2- R2I = | @C1 |+ R1I. et le galvanomètre ne mesure que R1I = @C2- @C1 - R2I.
En conséquence si le matériau 2 est inconnu et que l'on veut déterminer ses propriétés thermoélectriques on devra utiliser une méthode de zéro pour éliminer le terme R2I.
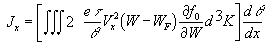
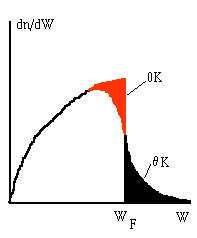
 et WF responsable d'un courant noté Jdiff+,
et l'autre correspondant à l'intégration entre WF
et WF+2.2k
et WF responsable d'un courant noté Jdiff+,
et l'autre correspondant à l'intégration entre WF
et WF+2.2k et responsable d'un courant
Jdiff-. On notera que Jdiff- fait apparaître une
polarité négative en AF et Jdiff+ une polarité
positive en AF. La prépondérance de l'un des deux termes
dépend de d3K qui dans les deux intégrales n'a pas
la même valeur puisque cette quantité représente, dans l'espace
des K, le volume compris entre la surface de Fermi et la surface d'énergie
WF-2.2k
et responsable d'un courant
Jdiff-. On notera que Jdiff- fait apparaître une
polarité négative en AF et Jdiff+ une polarité
positive en AF. La prépondérance de l'un des deux termes
dépend de d3K qui dans les deux intégrales n'a pas
la même valeur puisque cette quantité représente, dans l'espace
des K, le volume compris entre la surface de Fermi et la surface d'énergie
WF-2.2k , d'une part, et la surface de Fermi et celle
d'énergie WF+2.2k
, d'une part, et la surface de Fermi et celle
d'énergie WF+2.2k , d'autre part.
, d'autre part. 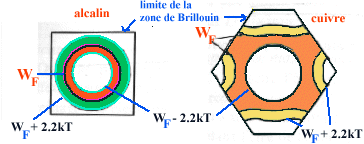
 |
 |