
Copyright
© 2000-2014
LHERBAUDIERE
12 pages à l'impression

18 mars 2013
 |
Copyright |
12 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 18 mars 2013 |
caractérisation (4/4): complément
| position du problème | les méthodes | |||
| électrostriction et piézoélectricité | un phénomène intéressant | |||
| les lois de Curie | 1881 | |||
| interprétation structurale | ||||
| phénomène de résonance du quartz | une lame métallisée | |||
| taille des lames et température | ||||
| les astuces | ||||
| une collection d'icônes pour visiter tout le site | ||||
capteur piézoélectrique de masse (ou d'épaisseur équivalente)
Position du problèmeMayer et Behrndt ont, les premiers, atteint une précision satisfaisante dans la pesée des monocouches en utilisant une microbalance de torsion utilisable sous ultra-vide. Les difficulté d'emploi et la fragilité de ces balances ont motivé des travaux qui ont conduit au développement d'un procédé précis, sensible et robuste, à savoir la microbalance à quartz vibrant en cisaillement d'épaisseur, issue des travaux initiaux de Sauerbrey et Lostis.Presque toutes les études concernant les couches minces impliquent la détermination de l'épaisseur où d'un paramètre équivalent. Parmi les méthodes permettant cette détermination on trouve la pesée qui donne l'épaisseur e en fonction de la masse déposée m selon la relation e =;m/soù s et
sont respectivement la surface et la masse volumique de la couche mince étudiée.
electrostriction et piézoélectricitéUn champ électrique polarise une substance diélectrique en y introduisant des moments dipolaires. Ce déplacement de charges, à partir de leurs positions d'équilibre, peut modifier les dimensions du solide : c'est l'électrostriction qui existe à un degré plus ou moins important pour tous les cristaux.
Effet piézoélectrique direct - lois de Curie (1881 Jean et Pierre Curie)Soit une lame rectangulaire définie comme sur la figure. Soit e parallèle à l'axe électrique Ox, L selon Oy axe mécanique et l selon Oz axe optique.
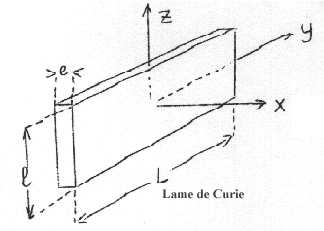
1ère loi :Si l'on applique Fx dans le sens de l'axe électrique, il apparait des quantités d'électricité sur les faces perpendiculaires à Ox. La charge Q sur la face x>0 est donnée par Qx = KFx, où K est une constante dépendant de la matière utilisée, mais indépendante des dimensions de la plaque.
2ème loi :Si l'on applique une force Fy dans la direction de l'axe mécanique, des charges apparaissent à nouveau sur les faces perpendiculaires à Ox, mais de signe opposé à celles du cas précédent. Q'x = - K Fy L/e. La constante K est appelée module piézoélectrique.
3ème loi :Les efforts mécaniques dans la direction de l'axe optique ne donnent lieu à aucun effet piézoélectrique.
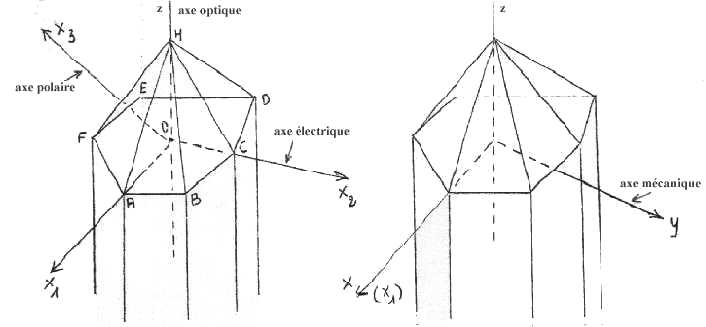
Interprétation qualitative structuraleL'aspect du monocristal est lié à la configuration de la maille cristalline; celle-ci comprend 3 molécules de SiO2 dont la projection sur un plan normal à l'axe optique est représentée par la figure ci-dessous dans laquelle les atomes d'oxygène sont légèrement plus petits que ceux de silicium.

 s
ds. Le mouvement obéit ainsi à l'équation
s
ds. Le mouvement obéit ainsi à l'équation  où c est la vitesse ou célérité du mouvement.
Dans le cas de mouvements sinusoïdaux, de période T, la périodicité
dans l'espace est la longueur d'onde
où c est la vitesse ou célérité du mouvement.
Dans le cas de mouvements sinusoïdaux, de période T, la périodicité
dans l'espace est la longueur d'onde  = cT
= cTphénomène de résonance du quartzLa résonance d'une lame est obtenue quand son épaisseur est un nombre entier de demi-longueurs d'onde, les faces terminales correspondant à des ventres de déplacement.
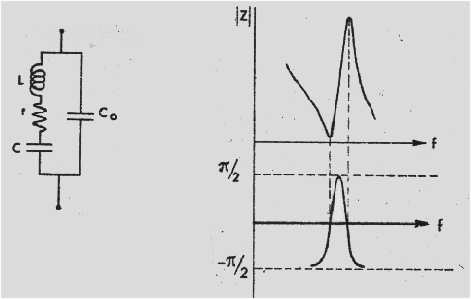
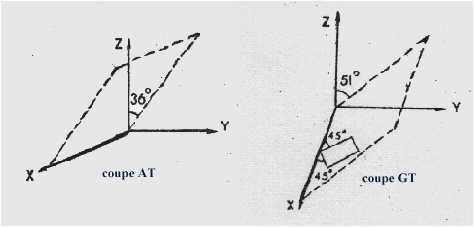
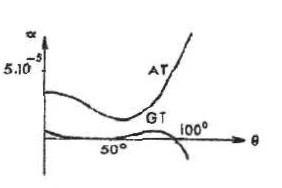
taille des lames et influence de la températureUn quartz piézoélectrique fournit un circuit équivalent avec un excellent facteur de surtension. C'est pourquoi on l'utilise dans les filtres et dans les oscillateurs électriques. Cependant la fréquence de résonance varie avec la température comme les propriétés mécaniques du cristal. On a cherché à obtenir un coefficient de température
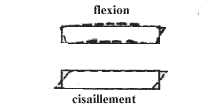
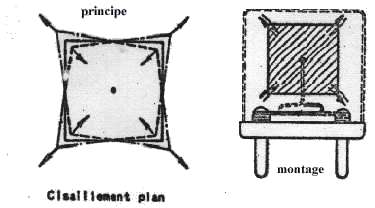
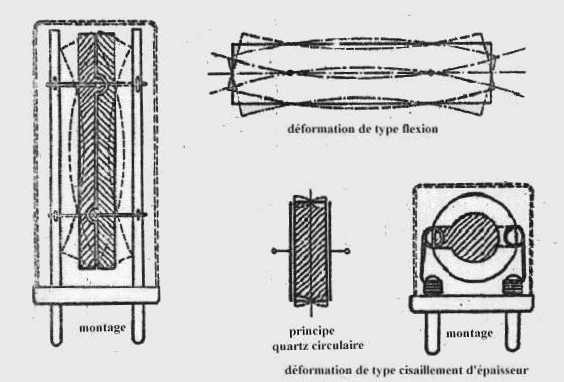
relation entre masse déposée et variation de fréquenceLes oscillations de cisaillement en épaisseur constituent un système d'ondes stationnaires transversales. Pour la vibration fondamentale, l'épaisseur du quartz représente 1/2 longueur d'onde. Si f est la fréquence correspondante on a donc
| Ainsi pour un quartz | AT | N = 1670 kHz.mm |
| BT | N = 2500 kHz.mm |
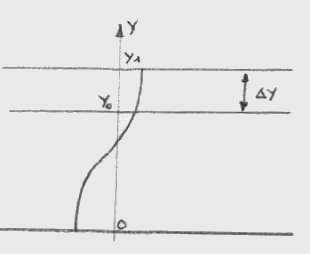
 la masse spécifique pour les milieux respectifs. En Y0 la
continuité des déplacements permet d'écrire u1
= u2 qui est une identité en t, d'où
la masse spécifique pour les milieux respectifs. En Y0 la
continuité des déplacements permet d'écrire u1
= u2 qui est une identité en t, d'où  1
=
1
=  2
2 l/l est
le tenseur des contraintes dans une seule direction, que l'on peut exprimer
ici par du/dy
l/l est
le tenseur des contraintes dans une seule direction, que l'on peut exprimer
ici par du/dy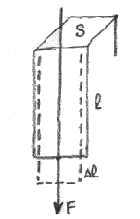
 0 la pulsation avant
que le cristal ne reçoive la couche nous avons, puisque Y0
doit être égal à une demi-longueur d'onde
0 la pulsation avant
que le cristal ne reçoive la couche nous avons, puisque Y0
doit être égal à une demi-longueur d'onde  0
0
 0 = 2
0 = 2 /T0
et
/T0
et  0 = T0v1
= v1/F0
0 = T0v1
= v1/F0 =
=
 0 +
0 + 
 soit
soit  m
est la masse de la couche et M
la masse vibrante du cristal (c'est à dire
en pratique la masse de la surface vibrante, surface identique en pratique
à celle du dépôt).
m
est la masse de la couche et M
la masse vibrante du cristal (c'est à dire
en pratique la masse de la surface vibrante, surface identique en pratique
à celle du dépôt). 0dY0
=
0dY0
=  1dY1.
1dY1.réalisation d'un capteur pour micropesée.Il suffit de disposer symétriquement de part et d'autre de l'évaporateur, le quartz vibrant et le support sur lequel on veut effectuer l'évaporation. Connaissant les surfaces des dépôts sur le quartz et le support et la variation de fréquence du quartz, il est facile de déterminer la masse déposée sur le quartz et donc celle déposée sur le substrat en admettant la proportionnalité entre surface et masse déposée. En pratique c'est d'ailleurs non la masse mais plus fréquemment l'épaisseur dY1 déposée qui intéresse l'expérimentateur, ce qui si l'on connait
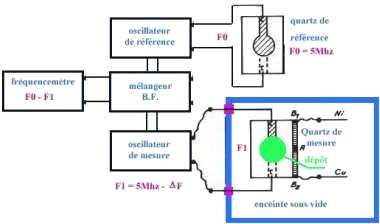
principe:
quartz retenuOn choisira un quartz de coupe AT, moins sensible à la température, et de fréquence relativement élevée (5 ou 10MHz en pratique). En effet pour un tel quartz la sensibilité
 F/
F/ m
est proportionnelle sensiblement à (F0)2, on a
donc avantage à choisir F0 élevé, mais la dérive
thermique croit aussi avec F0. Par ailleurs on admet dans la théorie
précédente que F0 et M0 sont invariants
pendant l'évaporation ce qui sous entend une valeur importante par rapport
aux variations
m
est proportionnelle sensiblement à (F0)2, on a
donc avantage à choisir F0 élevé, mais la dérive
thermique croit aussi avec F0. Par ailleurs on admet dans la théorie
précédente que F0 et M0 sont invariants
pendant l'évaporation ce qui sous entend une valeur importante par rapport
aux variations  F et
F et  m.
On montre aisément que l'erreur relative d(
m.
On montre aisément que l'erreur relative d( m)/
m)/ m
est proportionnelle à F0. Il en résulte que le meilleur
compromis se situe autour de 5 à 10 MHz.
m
est proportionnelle à F0. Il en résulte que le meilleur
compromis se situe autour de 5 à 10 MHz.
optimisation des électrodesLes différentes équations ci-dessus supposent implicitement que la totalité du domaine vibrant était recouverte par la couche. On constate, d'une part, que seul le domaine central de la lame participe à la vibration et que, d'autre part, lle diamètre minimum de la couche déposée sur le quartz vibrant validant les équations doit être de 5mm (dans le cas du quartz rectangulaire retenu de 12x14mm2). Dans ces conditions la couche déposée devra avoir un diamètre compris entre 5 et 10mm pour que la variation de fréquence soit liée de façon linéaire à la masse déposée, l'optimum étant de 8.5 mm.
problème de la températureLe procédé d'obtention des couches minces (vaporisation sous vide) entraine la présence au voisinage du quartz d'une source de chaleur susceptible de produire une élévation de la température de ce dernier. La fréquence de vibration variant avec la température, il est indispensable de maintenir constante la température du quartz durant la formation du dépôt si l'on veut obtenir une bonne fidélité (en particulier si l'on désire connaître en temps réel la masse déposée). Pour y parvenir on utilisera deux procédés :

limites pratiquesLa linéarité est limitée en raison de la variation de la masse vibrante pendant le dépôt, alors que l'expression calculée suppose que M0 ne varie pas. On peut cependant grâce à l'informatique calculer une correction en temps réel et réduire sensiblement cette non linéarité. La principale limitation provient du fait que le matériau déposé n'est pas du quartz et qu'il va progressivement introduire un amortissement croissant du coefficient de qualité du quartz dont il résultera une réduction de l'amplitude du signal et, in fine, un décrochage de l'oscillateur. En conséquence on sera limité pour l'amplitude du dépôt à une variation de fréquence de 0.1MHz pour des quartz de F0=5MHz.
 F
à
F
à  m, dès
lors qu'on reste dans la limite de 0.1MHz. Par contre il est exclus d'empiler
alternativement des matériaux métalliques et diélectriques,
car alors on constitue des capacités parasites néfastes à
la pertinence de la réponse.
m, dès
lors qu'on reste dans la limite de 0.1MHz. Par contre il est exclus d'empiler
alternativement des matériaux métalliques et diélectriques,
car alors on constitue des capacités parasites néfastes à
la pertinence de la réponse.Lostis P., Revue d'optique, 1 (1959) 1
 |