Lignes de transmission
Dans un autre document nous explicitons l'essentiel des procédés
de transmission, certains supposent une ligne entre l'émetteur et
le récepteur, qu'il s'agisse d'un cable de cuivre ou d'une fibre
optique, ce sont ces lignes, dont le rôle est alors essentiel, que
nous allons examiner ici. Nous allons montrer l'importance relative de la
longueur de la ligne et de la fréquence du signal dans le phénomène
de propagation.
PROPAGATION le long d'une ligne de transmission
partie (1/3)
1. phénomène de propagation
vitesse finie d'une onde
Jusqu'alors on ne s'est pas posé beaucoup la question. On a toujours
considéré que lorsque 2 points d'un circuit étaient réunis
par un simple conducteur, le signal était identique aux deux extrémités
des conducteurs au même instant. Pourtant dans la nature il semble bien
que les signaux se propagent avec une vitesse finie.
Par exemple :
- un caillou, lancé dans une mare, provoque un système d'ondes
qui se propagent en s'éloignant du point de chute du caillou,
- on a pu mesurer la vitesse du son, dans l'air c'est environ 340m/s
- la lumière se propage à 3.108m/s, c'est très
important, mais pas infini.
En ce qui concerne la propagation d'un signal électrique dans un cable
de cuivre, elle se fait aussi à une très grande vitesse, mais
ce n'est pas non plus l'infini. En conséquence la longueur de la ligne
est un paramètre qu'il faudra prendre en compte. Simultanément
la fréquence du signal intervient, ainsi une distance de 2000 km pour
un signal à 50 Hz est équivalente du point de vue du comportement
à 100 km à 1 kHz ou 1 cm à 1 GHz.
importance de la fréquence

Supposons un signal sinusoidal vA = V cos ( t
+
t
+  ) appliqué en A à
l'instant t à l'entrée d'une ligne de longueur l. Si on appelle
vf la vitesse de propagation, le signal mettra le temps t1
= l/vf pour parcourir la distance AB
) appliqué en A à
l'instant t à l'entrée d'une ligne de longueur l. Si on appelle
vf la vitesse de propagation, le signal mettra le temps t1
= l/vf pour parcourir la distance AB
donc vB = V cos [  ( t - t1)
+
( t - t1)
+  ] = V cos [
] = V cos [  (
t - l/vf) +
(
t - l/vf) +  ]
]

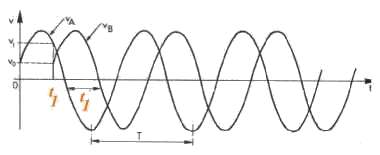
si t1/T est > 1, alors le phénomène de propagation
est important. Il est négligeable dans le cas contraire, en particulier
en régime continu dès lors que le régime transitoire est
achevé.
longueur d'onde
La figure précédente était une représentation temporelle
du signal (en A ou en B), si maintenant on regarde ce même signal à
un instant donné tout le long de la ligne, après le temps d'établissement
t1, on observe un ensemble ou une portion de sinusoïde.
Si x est la distance d'un point quelconque de la ligne par rapport à
A
v = V cos [  (t- x/vf)
+
(t- x/vf)
+  ] = v (t, x)
] = v (t, x)
En ce point on a le même signal qu'en A mais avec un retard x/vj.
Le signal est donc fonction de t et de x. Ce qui signifie que les équations
différentielles que l'on va écrire, pour décrire ce signal
dans un cas de figure donné, seront des équations aux dérivées
partielles par rapport aux deux variables x et t.
Si l' on regarde ce qui se passe pendant un temps égal à la période
T on constate que le signal a parcouru une longueur  = vj.T
= vj.T
v ( t, x) = V cos [ 2 (t/T - x/vfT) +
(t/T - x/vfT) + ] = V cos [ 2
] = V cos [ 2 (t/T - x/
(t/T - x/ )
+
)
+  ]
]
On voit que si x varie de  , la phase varie
de 2
, la phase varie
de 2 et le cosinus reprend
sa valeur initiale. Donc si l/
et le cosinus reprend
sa valeur initiale. Donc si l/ > 1 on a phénomène de propagation, c'est à dire soit
l est grand, soit l est petit ( donc
> 1 on a phénomène de propagation, c'est à dire soit
l est grand, soit l est petit ( donc  grand).
grand).
grandeurs spatiales et temporelles
En introduisant dans v(x,t) les quantités  = vj T longueur d'onde,
= vj T longueur d'onde,  =
=  /vj constante de propagation,
k =
/vj constante de propagation,
k =  /vj
nombre d'onde, on peut écrire
/vj
nombre d'onde, on peut écrire
v (t, x) = V cos (  t -
t -  x
+
x
+  ) = V cos [ 2
) = V cos [ 2 (
ft - kx ) +
(
ft - kx ) +  ] = V cos [ 2
] = V cos [ 2 (t/T
- x/
(t/T
- x/ ) +
) +  ]
]
et vj =  /
/ =
=  /T = f/k dans ces relations le numérateur représente
une grandeur spatiale et le dénominateur une grandeur temporelle.
Cette vitesse de phase vj est constante dans les lignes dites non
dispersives qui sont celles que nous allons étudier et auxquelles nous
assimilerons fréquemment les lignes réelles. Quand celles-ci seront
identifiées comme lignes dispersives on constatera que la vitesse de
phase n'y est pas constante.
/T = f/k dans ces relations le numérateur représente
une grandeur spatiale et le dénominateur une grandeur temporelle.
Cette vitesse de phase vj est constante dans les lignes dites non
dispersives qui sont celles que nous allons étudier et auxquelles nous
assimilerons fréquemment les lignes réelles. Quand celles-ci seront
identifiées comme lignes dispersives on constatera que la vitesse de
phase n'y est pas constante.
2. les lignes de transmission
quelques types de lignes
Le milieu diélectrique qui sépare les conducteurs (air, céramique,
téflon, ...) joue un rôle important dans la vitesse de propagation
du signal.
paramètres distribués

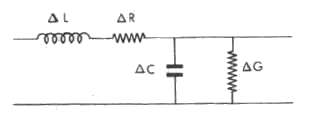
Considérons par exemple deux conducteurs parallèles. Ils sont
en influence électrostatique caractérisée par la capacité
C = Q/V , où Q est la charge portée par un conducteur et V la
ddp entre les deux conducteurs. Le courant parcourant la ligne crée un
champ d'induction magnétique B à son voisinage, avec réaction
sur le circuit qui lui a donné naissance (self induction), caractérisé
par L =  /I où
/I où  est le flux du vecteur B à travers la surface entourée par le
conducteur.
est le flux du vecteur B à travers la surface entourée par le
conducteur.
Donc un élément de ligne peut être caractérisé
par sa self, sa résistance série, sa capacité et sa conductance
parallèle. Si on met bout à bout des éléments de
ligne, les selfs s'ajoutent en série, tandis que les capacités
s'ajoutent en parallèle. Par suite on va caractériser une ligne
de transmission par ce qu'on va appeler les paramètres
distribués (L, R, C, G) rapportés à une unité
de longueur. Ainsi pour une longueur x on aura Lx, Rx, Cx, Gx. On négligera
le plus souvent R et G bien qu'en réalité ils produisent un affaiblissement.
capacité par unité
de longueur

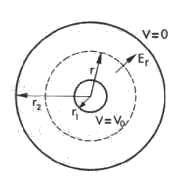
Soit un cable coaxial dont le conducteur extérieur, à la
masse, a un rayon r2 tandis que le conducteur intérieur de
rayon r1 est au potentiel V = Vo. Le conducteur intérieur
porte une charge Q par mètre qui crée à la distance r un
champ électrique radial Er lié au déplacement
électrique D =  o
o r
rE
r
( on rappelle E = - dV/dr =1/4

 o
o
q/r
2 dans le vide)
avec
 o
o = 1/36

10
9 F/m constante diélectrique du vide, et
 r
r
constante diélectrique relative du matériau isolant.
Le flux du vecteur déplacement
D à travers une surface
fermée S est égal à la charge contenue à l'intérieur
de cette surface.

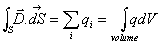
théorème de Gauss
ici la surface fermée est un cylindre de rayon r et de longueur
l,
comme
Er est radial le
flux à travers les faces extrêmes du cylindre est nul,
donc

= 2

r
lD
r
= Q
l et
Er
= Q/ 2

 r
r o
or
et comme le champ dérive d'un potentiel il vient
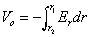
soit V
o = (Q/2

 o
o r
r)
Log (r
2/r
1)
et
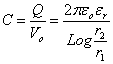
self par unité de longueur, cas du coaxial

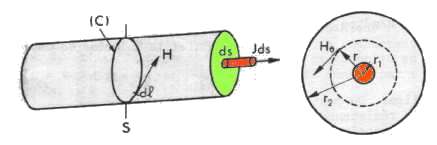
On va rappeler le théorème d'
Ampère
: la circulation du vecteur intensité du champ magnétique H le
long d'un contour fermé est égale à la somme des courants
entourés par ce contour
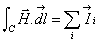
Or le champ magnétique s'exprime à partir du champ d'induction
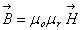
où µ
o
est la perméabilité du vide 4.10
7 henrys/m et µ
r
la perméabilité relative du milieu voisine de 1 (sauf pour les
matériaux ferromagnétiques).
Ici le contour est le cercle de rayon r, le champ est tangent à ce cercle,
la circulation est donc 2

rH
q
= I,

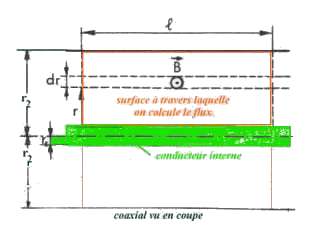
sachant que L =

/I . Le vecteur
induction magnétique est perpendiculaire à la surface qui sépare
le conducteur interne du conducteur externe (dans une coupe) donc on va écrire
que l'élément de flux d

= B dS avec dS =
l.dr (élément de surface autour de r et
d'épaisseur dr) en intégrant sur toute la surface donc entre r
1
et r
2 on obtient

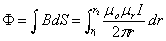
d'où
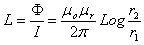
en
H/m
influence des pertes
Deux éléments interviennent en pratique pour générer
des pertes, d'une part, l'effet de peau et, d'autre part, l'imperfection de
la capacité réelle.
effet de peau : lorsque un signal de fréquence élevée
est véhiculé dans un conducteur on constate que les électrons
se concentrent statistiquement à la périphérie du conducteur,
tout se passe donc comme si le conducteur était ramené à
un tube creux de diamètre extérieur égal à celui
du conducteur, en d'autre termes la section utile est réduite et par
conséquent la
résistance accrue. On montre que l'épaisseur
de la zone de conduction (épaisseur de peau) s'exprime par
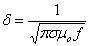
on en déduit évidemment la résistance à partir de
la relation classique
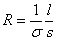
dans laquelle la section s s'exprimera à partir de l'expression de

et du rayon du conducteur.
condensateur réel : est en pratique un condensateur C avec une
conductance en parallèle caractérisée par un angle
de perte
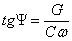
avec
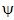
de l'ordre de 10
-4 pour les meilleurs diélectriques. On remplace
donc C par Y = G + jC

ligne bifilaire
Supposons une ligne bifilaire, c'est à dire constituée de 2 conducteurs
parallèles, de section circulaire de rayon R, distants de 2a (cable téléphonique).
Le même type de raisonnement que ci-dessus conduit à l'expression
de la capacité et de l'inductance par unité de longueur
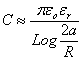
et
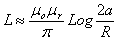
si a/R >>
1
microstrip
Soient 2 bandes conductrices planes de largeur b séparées par
un isolant d'épaisseur a (circuit imprimé typique)

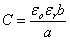
et
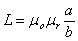
3. L'équation de propagation
équation d'onde

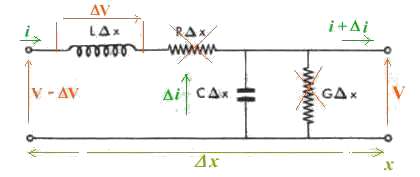
On examine un élément de ligne, supposée sans pertes, de
longueur

x qui se réduit
donc au schéma ci-dessus dans lequel la convention est que le sens croissant
des courants et tensions est de gauche à droite. La loi d'Ohm va donc
s'écrire simplement :
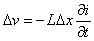
et
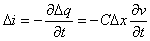
On fait tendre

x vers 0 et l'on admet
que les lois des circuits continuent à s'appliquer , il vient alors les
deux relations
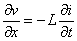
et
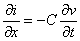
En dérivant
ces deux relations, la première par rapport à x et la seconde
par rapport à t, et en remplaçant ensuite dans les expressions
obtenues les termes di/dx pour la première et dv/dx pour la seconde par
leur expression ci-dessus on obtient deux relations homogènes
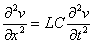
et

Ces deux équations doivent être résolues
simultanément.
Si l'on tient compte des pertes, on doit écrire pour les deux dipôles,
d'une part
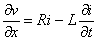
et
d'autre part
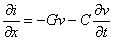
et par suite
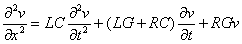
et
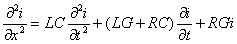
ce sont les
équations dites des télégraphistes
On montre en mathématiques qu'une solution de cette équation aux
dérivées partielles est du type
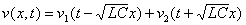
on va choisir v
1 et v
2 de type sinusoïdale ce qui
donne donc l'expression suivante
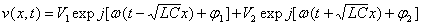
On obtient de la même manière i(x,t) en remplaçant
V
1 par I
1 et V
2 par I
2.
vitesse de phase
Si l'on considère le premier terme de la relation ci-dessus, mis sous
forme réelle, on s'aperçoit qu'on peut l'identifier au v de la
toute première relation du chapitre
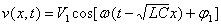
soit v = V cos [

(t - x/v

)
+

] on en déduit immédiatement
la vitesse de phase
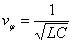
Si l'on considère le second membre de l'équation, on y voit apparaitre
une vitesse de phase égale à
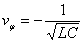
ce qui revient à dire que la solution générale de l'équation
d'onde est la somme de deux ondes de même fréquence se propageant
en sens inverse le long de la ligne. L'une est
l'onde
directe, l'autre est l'onde
réfléchie.
On montre que
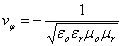
dans tous les cas de ligne examinés ici, donc
la propagation est indépendante
des dimensions de la ligne et de la fréquence du signal.
impédance et admittance
caractéristiques
Les relations solutions de l'équation d'onde doivent satisfaire en tout
point les lois des circuits que nous avons traduites par les relations
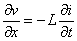
et
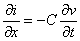
Nous allons
les vérifier en dérivant v(x,t) par rapport à x et i(x,t)
par rapport à t
on obtient
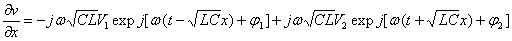
et
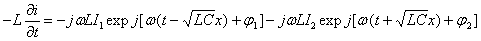
Pour que l'égalité
soit vérifiée entre ces deux expressions quels que soient t et
x il faut
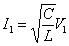
et
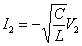
alors i(x,t) devient
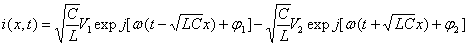

Donc, quels que soient x
et t, il existe un rapport constant entre le courant et la tension de l'onde
incidente et le même rapport au signe près pour l'onde réfléchie
: c'est
l'admittance caractéristique
de la ligne
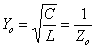
Pour un cable coaxial,
l'impédance caractéristique
est
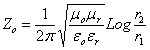

notons
par ailleurs que l'on peut aussi montrer que
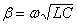
et écrire la solution de l'équation d'onde en conséquence.
puissance transportée
Rappelons tout d'abord quelques notions. La puissance instantanée dissipée
dans un dipôle à l'instant t,
Pinst
= v(t).i(t) n'a pas de sens physiquement, seule la valeur moyenne P
moy,
calculée sur un certain intervalle de temps, grand par rapport à
la période, sera significative.

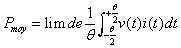
lorsque
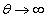
Soit un dipôle parcouru par i(t) = Io cos (

t
+

) aux bornes duquel on a
v(t) = Vo cos

t ce qu'on peut mettre sous
la forme exponentielle v(t) = Vo e
jwt
calculons S = (1/2)v*i = (1/2) Vo e
-jwt
Io e
+j(wt+ )
)
= (1/2) VoIo e
j
= (1/2) VoIo [cos

+
jsin

]
le conjugué de S s'écrit S* = (1/2) vi* = (1/2) VoIo [cos

-
jsin

]
d'où (1/2)[ S + S*] = (1/2) IoVo cos

= (1/4) [vi* + v*i] est la puissance moyenne dissipée dans le dipôle
ce que l'on peut vérifier en effectuant l'intégration.
Donc la puissance qui se propage le long de la ligne est
P
=(1/4) [vi* + v*i] si l'on remplace v et i par les premiers termes
des équations donnant v(x,t) et i(x,t) on obtient
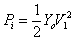
puissance que propage l'onde incidente vers les x croissants et de même
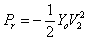
est la puissance
propagée par l'onde réfléchie vers les x décroissants.
On remarque que ces puissances sont constantes quel que soit x. Si l'on avait
tenu compte des pertes, on aurait en pratique une expression du type
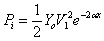
où
a est un coefficient d'atténuation.
La puissance transportée diminuerait alors de manière exponentielle
en fonction de x, c'est à dire lorsqu'on s'éloigne de la source.
Il en serait évidemment de même pour la puissance réfléchie.






 t
+
t
+  ) appliqué en A à
l'instant t à l'entrée d'une ligne de longueur l. Si on appelle
vf la vitesse de propagation, le signal mettra le temps t1
= l/vf pour parcourir la distance AB
) appliqué en A à
l'instant t à l'entrée d'une ligne de longueur l. Si on appelle
vf la vitesse de propagation, le signal mettra le temps t1
= l/vf pour parcourir la distance AB ( t - t1)
+
( t - t1)
+  ] = V cos [
] = V cos [  (
t - l/vf) +
(
t - l/vf) +  ]
]


 (t- x/vf)
+
(t- x/vf)
+  ] = v (t, x)
] = v (t, x) = vj.T
= vj.T (t/T - x/vfT) +
(t/T - x/vfT) + ] = V cos [ 2
] = V cos [ 2 (t/T - x/
(t/T - x/ )
+
)
+  ]
] , la phase varie
de 2
, la phase varie
de 2 et le cosinus reprend
sa valeur initiale. Donc si l/
et le cosinus reprend
sa valeur initiale. Donc si l/ > 1 on a phénomène de propagation, c'est à dire soit
l est grand, soit l est petit ( donc
> 1 on a phénomène de propagation, c'est à dire soit
l est grand, soit l est petit ( donc  grand).
grand).
 = vj T longueur d'onde,
= vj T longueur d'onde,  /vj constante de propagation,
k =
/vj constante de propagation,
k =  t -
t -  x
+
x
+  ) = V cos [ 2
) = V cos [ 2 (
ft - kx ) +
(
ft - kx ) +  ] = V cos [ 2
] = V cos [ 2 (t/T
- x/
(t/T
- x/ ) +
) +  ]
]
 /
/ =
=  /T = f/k dans ces relations le numérateur représente
une grandeur spatiale et le dénominateur une grandeur temporelle.
Cette vitesse de phase vj est constante dans les lignes dites non
dispersives qui sont celles que nous allons étudier et auxquelles nous
assimilerons fréquemment les lignes réelles. Quand celles-ci seront
identifiées comme lignes dispersives on constatera que la vitesse de
phase n'y est pas constante.
/T = f/k dans ces relations le numérateur représente
une grandeur spatiale et le dénominateur une grandeur temporelle.
Cette vitesse de phase vj est constante dans les lignes dites non
dispersives qui sont celles que nous allons étudier et auxquelles nous
assimilerons fréquemment les lignes réelles. Quand celles-ci seront
identifiées comme lignes dispersives on constatera que la vitesse de
phase n'y est pas constante.


 /I où
/I où  est le flux du vecteur B à travers la surface entourée par le
conducteur.
est le flux du vecteur B à travers la surface entourée par le
conducteur.

 o
o rEr
( on rappelle E = - dV/dr =1/4
rEr
( on rappelle E = - dV/dr =1/4
 o
q/r2 dans le vide)
o
q/r2 dans le vide)  o = 1/36
o = 1/36 109 F/m constante diélectrique du vide, et
109 F/m constante diélectrique du vide, et  r
constante diélectrique relative du matériau isolant.
r
constante diélectrique relative du matériau isolant.
 = 2
= 2 rlDr
= Ql et Er
= Q/ 2
rlDr
= Ql et Er
= Q/ 2
 r
r or
or
 o
o r)
Log (r2/r1)
r)
Log (r2/r1) 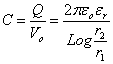


 rHq
= I,
rHq
= I, 

 /I . Le vecteur
induction magnétique est perpendiculaire à la surface qui sépare
le conducteur interne du conducteur externe (dans une coupe) donc on va écrire
que l'élément de flux d
/I . Le vecteur
induction magnétique est perpendiculaire à la surface qui sépare
le conducteur interne du conducteur externe (dans une coupe) donc on va écrire
que l'élément de flux d = B dS avec dS = l.dr (élément de surface autour de r et
d'épaisseur dr) en intégrant sur toute la surface donc entre r1
et r2 on obtient
= B dS avec dS = l.dr (élément de surface autour de r et
d'épaisseur dr) en intégrant sur toute la surface donc entre r1
et r2 on obtient 
 et du rayon du conducteur.
et du rayon du conducteur. de l'ordre de 10-4 pour les meilleurs diélectriques. On remplace
donc C par Y = G + jC
de l'ordre de 10-4 pour les meilleurs diélectriques. On remplace
donc C par Y = G + jC
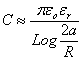 et
et 


 x qui se réduit
donc au schéma ci-dessus dans lequel la convention est que le sens croissant
des courants et tensions est de gauche à droite. La loi d'Ohm va donc
s'écrire simplement :
x qui se réduit
donc au schéma ci-dessus dans lequel la convention est que le sens croissant
des courants et tensions est de gauche à droite. La loi d'Ohm va donc
s'écrire simplement :  x vers 0 et l'on admet
que les lois des circuits continuent à s'appliquer , il vient alors les
deux relations
x vers 0 et l'on admet
que les lois des circuits continuent à s'appliquer , il vient alors les
deux relations  (t - x/v
(t - x/v )
+
)
+ ] on en déduit immédiatement
la vitesse de phase
] on en déduit immédiatement
la vitesse de phase 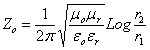

 t
+
t
+  ) aux bornes duquel on a
v(t) = Vo cos
) aux bornes duquel on a
v(t) = Vo cos  t ce qu'on peut mettre sous
la forme exponentielle v(t) = Vo ejwt
t ce qu'on peut mettre sous
la forme exponentielle v(t) = Vo ejwt )
= (1/2) VoIo ej
)
= (1/2) VoIo ej = (1/2) VoIo [cos
= (1/2) VoIo [cos +
jsin
+
jsin ]
] -
jsin
-
jsin ]
]  = (1/4) [vi* + v*i] est la puissance moyenne dissipée dans le dipôle
ce que l'on peut vérifier en effectuant l'intégration.
= (1/4) [vi* + v*i] est la puissance moyenne dissipée dans le dipôle
ce que l'on peut vérifier en effectuant l'intégration.

