1. Réflexion sur une charge

influence d'une impédance branchée sur la ligne

Nous avons vu qu'en tout point de la ligne le rapport entre v et i de l'onde incidente est constant et égal à l'impédance caractéristique de la ligne.

v(x, t) = Zo i(x, t)

Si en bout de ligne on branche une impédance de charge Z_T, la loi d'Ohm nous impose la relation, pour x = l,

v(l, t) = Z_T i (l, t)

S'il n'y avait que l'onde incidente, les deux relations devraient être vérifiées simultanément par v et i, ce qui n'est possible que si ZT = Zo.

Cependant on sait que la solution générale de l'équation d'onde est la somme de deux solutions particulières, l'une représentant l'onde incidente, l'autre l'onde réfléchie. Cette solution doit être valable pour tout x et en particulier pour x=l, soit :

V₁exp j (t - l + ₁) + V₂exp j (t + l + ₂) = Z_TYo V₁exp j (t - l +₁) - Z_TYo V₂exp j (t + l + ₂)

En simplifiant les deux membres de cette équation par exp jt on obtient une équation complexe indépendante du temps, dans laquelle les données sont V₁ et ₁, amplitude et phase à l'origine de l'onde incidente, et V₂ et ₂, les mêmes quantités à l'origine de l'onde réfléchie. On peut résoudre le problème en séparant l'équation en deux parties, réelle et imaginaire. Cela veut dire en pratique que l'existence d'une impédance de charge en bout de ligne entraine nécessairement une réflexion à l'extrémité de la ligne (comme le caillou lancé dans la mare génère une onde qui va se réfléchir sur la rive) de telle sorte que la loi d'Ohm soit vérifiée sur la charge.

changement d'axe

Les équations écrites jusqu'ici supposaient un axe des x dont l'origine soit le générateur et orienté vers le récepteur. En pratique on va s'intéresser à ce qui se passe au voisinage du récepteur et il est d'ailleurs fréquent que l'on ne sache où se trouve le générateur, c'est à dire que l soit inconnue. Il semble alors judicieux de procéder à une opération astucieuse qui permettra d'éliminer l dans les équations. Cela est obtenu en opérant un changement d'axe judicieux, c'est à dire en choisissant un axe z dont l'origine est la charge et qui soit orienté vers le générateur.
Ainsi un point d'abscisse x devient z = l - x

Notons que par suite d/dz = - d/dx et d²/dz² = d²/dx²
Il vient donc
v (z, t) = V₁exp j (t + z + ₁) + V₂exp j (t - z + ₂) avec ₁ et ₂ dans lesquels on a intégré la constante l et qui sont donc les nouvelles phases à l'origine (mais au niveau du récepteur maintenant).
On fait évidemment la même transformation pour le courant qui devient i (z, t). La vitesse de phase de l'onde incidente est maintenant négative v_j = dz/dt = - / < 0 tandis que symétriquement celle de l'onde réfléchie devient positive dans ce nouveau système d'axe.

coefficient de réflexion

La loi d'Ohm en z = 0 devient v(0, t) = Z_T i (0,t) ce qui dans l'équation générale donne
V₁ exp j₁ + V₂ exp j₂ = Z_IYoV₁ exp j₁ - Z_TYoV₂ exp j₂ en mettant V₁ expj₁ en facteur on obtient

(1)

Ce terme qui représente le rapport entre la tension réfléchie et la tension de l'onde incidente en z = 0 est appelé coefficient de réflexion en tension

On en tire pour l'expression (1) 1 + = Z_TYo [ 1 - ] soit en posant z_T = Z_TYo = Z_T/Zo impédance réduite terminale.

Notons les cas particuliers

si ZT = Zo	alors zT = 1	= 0	ligne adaptée
si ZT = 0	court circuit	zT = 0	= - 1
si ZT infini	ligne ouverte		= + 1

Dans les deux derniers cas l'onde réfléchie a même amplitude que l'onde incidente, mais elle est déphasée de dans le cas du court-circuit terminal ou en phase pour la ligne ouverte.

On peut de même définir un coefficient de réflexion en courant qui a même module que mais est déphasé de

autres relations

On peut exprimer les mêmes quantités i et v par d'autres relations en introduisant dans les expressions ci-avant de v(z, t) ou de i(z, t)

(2)


En z=0 on mesure v (0, t) = V_T expjwt = V₁ expjj₁ ( 1 + ) expjt , de même pour i (0, t)

La mesure de V_T et I_T est techniquement aisée, et donc, même en ignorant la source (V₁ et f₁), on voit qu'il sera possible à partir de la mesure en z = 0 d'exprimer v (z, t) en tout point en remplaçant V₁ expj₁ par son expression tirée de la relation ci-dessus. Il en est de même pour . On obtient finalement les expressions

---

2. ondes stationnaires

Les 2 ondes incidente et réfléchie sont parfaitement définies l'une par rapport à l'autre. En particulier en un point donné elles présentent une différence de phase constante dans le temps qui dépend du coefficient de réflexion, c'est à dire de la charge (cf. équation (2) ci-dessus). Cette différence de phase dépend aussi de z, en fait de (2z) qui représente le temps mis pour l'onde pour aller de z à la charge et en revenir. On a donc un phénomène d'ondes stationnaires (cf corde vibrante ou phénomène d'interférence lumineuse) de périodicité l/2.

position des maxima et des minima

L'un des éléments caractéristiques de ce système d'ondes stationnaires c'est évidemment d'avoir des maxima et des minima d'amplitude en des points bien définis que l'on peut identifier. Notons qu'à l'inverse de chacune des ondes directe et réfléchie le système d'onde stationnaire ne possède généralement pas de minima nuls, puisqu'ils correspondent à la différence entre les amplitudes de ces ondes qui sont généralement différentes, donc de différence non nulle. Reprenons la relation (2) donnant v(z, t) soit V(z) expjwt, écrivons |V(z)|² = v(z, t)v*(z, t) où v* est la quantité conjuguée obtenue en remplaçant j par -j.

par ailleurs =||expj d'où |V(z)|² = V₁² [ 1 + ||[expj(- 2z) + exp-j( - 2z)] + ||²]

si on remplace les exp par des cos et en se rappelant la relation trigonométrique 2cos a = e^a+e^-a

|V(z)|² = V₁² [ 1 + 2||cos (- 2z) + ||²]

Cette expression est maximale pour z = z_M tel que cos (- 2z) = 1 soit (- 2z) = + ou - 2n avec n entier

à laquelle correspond |V(z)|^2_max = V₁² [1 + ||]²

et minimale pour cos ( - 2z) = -1 soit (- 2z) = + ou - 2(n+1) soit
à laquelle correspond |V(z)|^2_min = V₁² [1 - ||]²

En choisissant n = 0 on va aisément pouvoir calculer la position du premier maxima ou du premier minima par rapport à la charge.

---

TOS taux d'ondes stationnaires

On caractérise les ondes stationnaires par le TOS précisons que puisque || < 1 S sera toujours > 1 (ou égal à 1)
et bien entendu || = S-1/S+1

impédance ramenée z_R(z)

Une portion de ligne est équivalente à un quadripôle



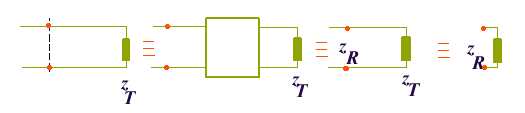
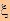En tout point de la ligne on peut assimiler tout ce qui est à droite à une impédance z_R telle que z_R(z) = v(z, t)/i(z, t) Comme v et i varient de la même façon en fonction du temps z_R sera indépendante du temps et seulement dépendante de l'abscisse. on en déduit que z_R varie périodiquement avec des maxima et des minima et en coordonnées réduites on a _Rmax = S et 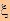_Rmin = 1/S

En utilisant les expressions sinusoïdales de v et de i on obtient ce qu'on peut écrire en utilisant les expressions réduites la périodicité est la même que celle de v(z), soit /2.

On a évidemment une expression semblable pour l'admittance ainsi que pour l'admittance réduite

conséquence

Si, sur une ligne donnée, on fait varier la fréquence du signal, l'impédance ramenée à l'entrée de la ligne va varier, et donc passer successivement par des maxima et des minima. Cette propriété est utilisée pour localiser un défaut sur une ligne : sur une ligne enterrée par exemple on n'a pas aisément accès en tout point, or un défaut c'est équivalent à une charge non adaptée (ligne ouverte ou court-circuit) située à une distance z₀ inconnue du point d'accès A. On mesure donc l'impédance ramenée en A

On fait varier , pour ₀ on obtient b₀₀ et on a un maximum d'impédance ramenée , correspondant à la distance z₀. Si on augmente , le système d'ondes stationnaires se resserre et pour ₁ on a un nouveau maximum correspondant à la même distance.

On dispose alors de deux équations à deux inconnues z₀ et que l'on peut résoudre aisément. Il vient . La connaissance des fréquences permet alors celle de l'emplacement du défaut.

quelques cas particuliers

ligne adaptée : Z_T = Z₀ ligne terminée par son impédance caractéristique, z_R(z) = Z₀

ligne en court circuit: ce qu'on appelle souvent un stub

Z_T = 0 d'où z_R(z) = jZ₀tgz et impédance réduite jtgz

ligne ouverte:

Z_T infinie z_R(z) = -jZ₀cotgz impédance réduite -jcotgz

Les lignes terminées par un court-circuit ou un circuit ouvert permettent de réaliser une impédance purement imaginaire de n'importe quelle valeur (entre moins l'infini et plus l'infini). On va donc les utiliser fréquemment.