
Copyright
© 2000-2015
LHERBAUDIERE
7 pages à l'impression

22 mars 2013
 |
Copyright |
7 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 22 mars 2013 |
Lignes
de transmission
Adaptation
partie (3/3)
| puissance transmise à la charge | le problème de l'adaptation | |||
| réalisation de l'adaptation par stub | la solution | |||
| principe de l'abaque de Smith | une méthode graphique (quand on n'a pas d'ordinateur) |
|||
| utilisation de l'abaque de Smith | les exemples basiques | |||
| une collection d'icônes pour visiter tout le site | ||||

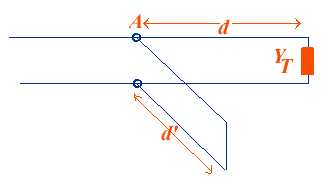
 t fournie
par un générateur d'impédance interne Zi, une
ligne d'impédance caractéristique Z0 de constante de
propagation
t fournie
par un générateur d'impédance interne Zi, une
ligne d'impédance caractéristique Z0 de constante de
propagation  et de longueur
l grande devant
et de longueur
l grande devant  , une charge ZT
, une charge ZTZi
= Z0 = ZT, dans ce cas zR
= Z0 quelle que soit l, il n'y a pas d'onde
réfléchie et Pi = 1/2 Y0 VT2.
Toute la puissance est transmise à la charge. |
Zi
= Z0 différente de ZT, l'onde
incidente transporte Pi
= 1/2 Y0 V12 et l'onde réfléchie
ramène vers le générateur Pr
= 1/2Y0 V22, où V1
et V2 sont les amplitudes respectives des ondes incidente
et réfléchie. P consommée = Pi
- Pr |
Zi
différente de Z0 = ZT. La
charge est adaptée donc toute l'énergie transmise est absorbée
par la charge, mais le générateur ne l'est pas, ce qui signife
qu'il ne transmet pas à la ligne toute la puissance qu'il est susceptible
de fournir |
Zi
différente de Z0 différente de ZT.
C'est le cas le plus défavorable à éviter absolument,
car la réflexion partielle s'effectue aussi bien au niveau de la
charge que du générateur, d'où un systèmes
d'ondes stationnaires extrêmement complexe! |

 (z) varie
périodiquement comme ZR
(z) varie
périodiquement comme ZR (z) = |
(z) = | |
expj
|
expj exp(-2j
exp(-2j z)
or
z)
or  (z) étant un nombre
complexe on va l'écrire sous la forme
(z) étant un nombre
complexe on va l'écrire sous la forme  (z)
= a + jb et l'impédance réduite s'exprime alors par
(z)
= a + jb et l'impédance réduite s'exprime alors par  représenté par un point R d'abscisse a et d'ordonnée
b.
représenté par un point R d'abscisse a et d'ordonnée
b.
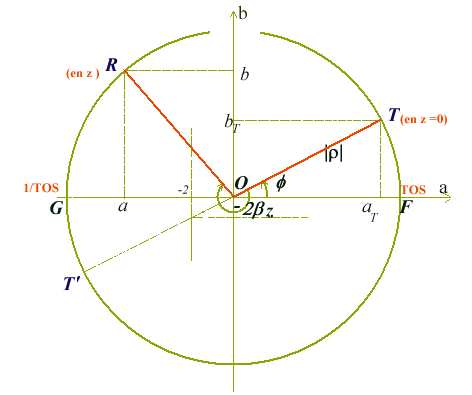
 T = |r|exp jj
= aT + jbT,
T = |r|exp jj
= aT + jbT,  T
est représenté dans le plan complexe par le point T, et le coefficient
T
est représenté dans le plan complexe par le point T, et le coefficient
 (z) en tout point z sera représenté
par un point du cercle dont le rayon est |
(z) en tout point z sera représenté
par un point du cercle dont le rayon est | |
|
 + 1)
donc < 1. De plus ils coupent tous l'axe réel au point 1 et
+ 1)
donc < 1. De plus ils coupent tous l'axe réel au point 1 et  -1/
-1/ +1
+1

 = constante, coupent l'axe réel
a, c'est donc sur cette horizontale que l'on trouvera la graduation en
= constante, coupent l'axe réel
a, c'est donc sur cette horizontale que l'on trouvera la graduation en .
. = 0.5 et du cercle x =
0.3 on a le point R représentatif de l'impédance zR
= 0.5 + j 0.3
= 0.5 et du cercle x =
0.3 on a le point R représentatif de l'impédance zR
= 0.5 + j 0.3
mesure du coefficient rLa mesure du coefficient de réflexion se fait aisément en passant du point R au point T par une rotation d'un angle
 - 2
- 2 z autour d'un cercle dont
le centre est le centre de l'abaque et le rayon |
z autour d'un cercle dont
le centre est le centre de l'abaque et le rayon | |.
Il suffit de mesurer son rayon avec une règle graduée (et de ne
pas oublier que le cercle pourtour de l'abaque a un rayon = 1, ce qui sur votre
écran correspond à un certain nombre de centimètres) |
|.
Il suffit de mesurer son rayon avec une règle graduée (et de ne
pas oublier que le cercle pourtour de l'abaque a un rayon = 1, ce qui sur votre
écran correspond à un certain nombre de centimètres) | |
représente la distance OR ou OT.
|
représente la distance OR ou OT.
mesure deet longueur de ligne
 c'est l'angle de OT avec
l'axe a. Pour aller de R à T on tourne de - 2
c'est l'angle de OT avec
l'axe a. Pour aller de R à T on tourne de - 2 z
et sur la ligne on se déplace de z.
z
et sur la ligne on se déplace de z. = 2
= 2 /
/ et
qu'un déplacement de z =
et
qu'un déplacement de z =  /2 correspond
à une rotation de 2
/2 correspond
à une rotation de 2 ,
c'est à dire un tour complet de cercle. On a donc gradué à
l'extérieur du cercle de rayon 1, une graduation spéciale qui
permet de lire les fractions de longueur d'onde dont on se déplace. La
graduation est double puisqu'on peut se déplacer sur la ligne, soit en
allant vers le générateur (sens des aiguilles d'une montre), soit
à l'inverse vers le récepteur (attention il y a une chance sur
deux de se tromper!). Cette graduation est en coordonnée réduite
: 1 tour correspond à
,
c'est à dire un tour complet de cercle. On a donc gradué à
l'extérieur du cercle de rayon 1, une graduation spéciale qui
permet de lire les fractions de longueur d'onde dont on se déplace. La
graduation est double puisqu'on peut se déplacer sur la ligne, soit en
allant vers le générateur (sens des aiguilles d'une montre), soit
à l'inverse vers le récepteur (attention il y a une chance sur
deux de se tromper!). Cette graduation est en coordonnée réduite
: 1 tour correspond à /2
soit 0.5. Il faudra multiplier par
/2
soit 0.5. Il faudra multiplier par  pour
avoir la longueur z en mètres.
pour
avoir la longueur z en mètres.
utilisation pratiqueSoit une ligne Z0 = 50
 terminée par une charge
ZT = 100 + j 25
terminée par une charge
ZT = 100 + j 25  , on cherche |
, on cherche | |
et le TOS.
|
et le TOS. = 0.36
= 0.36 de OT avec l'axe
horizontal est obtenu en prolongeant OT jusqu'à la graduation extérieure,
on lit 0.226. Sur l'axe horizontal (à droite) on lit 0.25, on tourne
donc de [0.25 - 0.226] = 0.024
de OT avec l'axe
horizontal est obtenu en prolongeant OT jusqu'à la graduation extérieure,
on lit 0.226. Sur l'axe horizontal (à droite) on lit 0.25, on tourne
donc de [0.25 - 0.226] = 0.024 ,
,  correspond à 2
correspond à 2 donc
donc  = 0.024x2
= 0.024x2 /0.5
= 0.096
/0.5
= 0.096  radian
radian (côté
droit >1) on trouve TOS = 2.15 et bien entendu son inverse 0.46 = 1/TOS
(côté
droit >1) on trouve TOS = 2.15 et bien entendu son inverse 0.46 = 1/TOS = c/f =
6 m. On sait qu'aux maxima et minima de V et I sur la ligne l'impédance
est purement réelle (son point représentatif est celui qui nous
a permis de trouver le TOS et son inverse). Un déplacement de T jusqu'au
premier maximum (point F) correspond à un déplacement angulaire
de
= c/f =
6 m. On sait qu'aux maxima et minima de V et I sur la ligne l'impédance
est purement réelle (son point représentatif est celui qui nous
a permis de trouver le TOS et son inverse). Un déplacement de T jusqu'au
premier maximum (point F) correspond à un déplacement angulaire
de  (déjà calculé)
et une distance dM = [0.25 - 0.226]
(déjà calculé)
et une distance dM = [0.25 - 0.226] = 0.024
= 0.024 = 0.144m
= 0.144m /4 plus loin, soit
ici 1.5m plus loin dm = 1.644m, les suivants étant décalés
de
/4 plus loin, soit
ici 1.5m plus loin dm = 1.644m, les suivants étant décalés
de  /2.
/2. /4 de zT est
yT, c'est à dire que le point représentatif de yT
est le point T' symétrique de T. Il suffit alors de lire quels sont les
cercles passant par T' pour connaitre yT puis YT = yT/Z0.
/4 de zT est
yT, c'est à dire que le point représentatif de yT
est le point T' symétrique de T. Il suffit alors de lire quels sont les
cercles passant par T' pour connaitre yT puis YT = yT/Z0. constitué d'un morceau de ligne
d'impédance caractéristique 300
constitué d'un morceau de ligne
d'impédance caractéristique 300  ,
,
 ,
aura une longueur de 0.426
,
aura une longueur de 0.426 .
.
adaptationOn donne TOS = 4.48, distance du premier minimum à la charge 6 cm, fréquence 300MHz (soit
 =1.5m), Z0 = 50
=1.5m), Z0 = 50 
 à partir de(zT =0.24 - 0.24j), on peut alors tracer
le symétrique yT. On sait que tout point de la ligne est sur
le cercle passant par T et T' et de centre O (cercle vert), mais qu'il y a 2
points où ce cercle coupe celui
à partir de(zT =0.24 - 0.24j), on peut alors tracer
le symétrique yT. On sait que tout point de la ligne est sur
le cercle passant par T et T' et de centre O (cercle vert), mais qu'il y a 2
points où ce cercle coupe celui  = 1 (les points I et J de la figure) en ces points on a YR = Y0
+ jB et YR = Y0 - JB.
= 1 (les points I et J de la figure) en ces points on a YR = Y0
+ jB et YR = Y0 - JB. = 0). Sa longueur
est définie en allant de K vers A (dans le sens inverse des aiguilles
d'une montre) soit 3/4 de tour environ et très exactement 0.415
= 0). Sa longueur
est définie en allant de K vers A (dans le sens inverse des aiguilles
d'une montre) soit 3/4 de tour environ et très exactement 0.415 ce qui correspond ici à 62.4 cm.
ce qui correspond ici à 62.4 cm. 

 /8,
mais l'ensemble pourra être placé n'importe où sur
la ligne.
/8,
mais l'ensemble pourra être placé n'importe où sur
la ligne. 

 = 1 (orange
sur la figure)
= 1 (orange
sur la figure) 
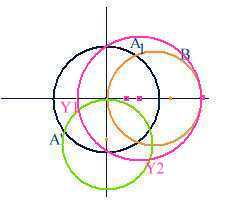
 /8
dans le sens inverse des aiguilles d'une montre, partant de A1 on va arriver
en A'. De même tout point B du cercle orange
par un même déplacement va se retrouver sur un point du cercle
vert. Or quand on se déplace ainsi on est arrivé sur la ligne
au point A2 où se trouve le stub 2.
/8
dans le sens inverse des aiguilles d'une montre, partant de A1 on va arriver
en A'. De même tout point B du cercle orange
par un même déplacement va se retrouver sur un point du cercle
vert. Or quand on se déplace ainsi on est arrivé sur la ligne
au point A2 où se trouve le stub 2.  ) et, par suite,
on saura faire l'adaptation en ce point à l'aide d'un stub 1 de longueur
adéquate.
) et, par suite,
on saura faire l'adaptation en ce point à l'aide d'un stub 1 de longueur
adéquate.  |