Effet de l'épaisseur sur les propriétés
Après avoir rappelé les notions de base de la physique du solide
massif examinons la résistivité du matériau à l'état
de couche mince en nous attachant à mettre en exergue les spécificités
qui résultent de deux facteurs principaux, à savoir
- l'épaisseur équivalente d'une part,
- et le mode de préparation d'autre part (c'est à dire le
processus qui influe sur les imperfections du réseau).
Pour cela nous allons nous appuyer sur une modélisation,
reposant sur diverses hypothèses de départ, et dérivant
des schémas que nous avons rencontrés dans le matériau
massif. Cependant, il importe de savoir qu'il n'existe pas aujourd'hui de modèle
mathématique général permettant de représenter de
manière correcte le comportement d'une couche mince quelconque. Il y
a en effet beaucoup trop de facteurs expérimentaux insuffisamment connus
ou maîtrisés entrant en jeu. Aussi le modèle présenté
ici est celui qui donne à peu près satisfaction en particulier
dans les applications développées dans les chapitres précédents.
Nous en indiquerons les limites ainsi que les diverses tentatives récentes
engagées pour le perfectionner.
 En pratique,
il sera surtout essentiel de retenir les grandes conséquences
que l'on peut en dégager, en ce qui concerne le développement
d'applications technologiques des couches minces dans des capteurs de mesures
physiques, en gardant constamment à l'esprit qu'il faut toujours être
très prudent quand on veut employer des couches minces, car il y a
souvent des comportements imprévus mettant en défaut les théories
les plus élaborées.
En pratique,
il sera surtout essentiel de retenir les grandes conséquences
que l'on peut en dégager, en ce qui concerne le développement
d'applications technologiques des couches minces dans des capteurs de mesures
physiques, en gardant constamment à l'esprit qu'il faut toujours être
très prudent quand on veut employer des couches minces, car il y a
souvent des comportements imprévus mettant en défaut les théories
les plus élaborées.
phénoménologie
Nous supposerons que nous savons, ce qui n'est pas toujours
facile à faire, fabriquer des couches minces de structure reproductible
et indépendante de l'épaisseur. Il est alors possible d'examiner
le seul effet d'une variation d'épaisseur sur la conductivité
du matériau.
Cette contrainte impose des conditions expérimentales reproductibles
et donc une maîtrise parfaite de ces conditions que seuls une très
grande compétence de l'opérateur, doublée d'un automatisme
hypersophistiqué et d'un matériel de haute qualité, permettent
d'obtenir.
Il faut en outre se rappeler qu'une couche mince se constitue, par dépôt
sur un substrat, selon un processus de dépôt statistique
auquel se combine une migration superficielle et des points de germination
initiaux apparemment aléatoires (mais en fait liés à la
qualité de l'état de surface du substrat). Il en résulte
que jusqu'à une certaine épaisseur moyenne (dont la valeur est
très sensible à ces conditions de préparation ) se situant
souvent au delà de 20 nm, mais parfois en deçà de 2 nm,
la couche mince ne peut être considérée comme présentant
une continuité suffisante pour que la conductivité obéisse
à un schéma voisin de celui décrit dans le matériau
massif.
Nous ne nous intéresserons donc pas aux couches très minces pour
lesquelles le modèle que nous allons décrire est inadéquat.
Notons simplement qu'il existe des modèles de conduction qui semblent
s'appliquer aux couches lacunaires (celui développé par Hopkins
par ex), mais ces couches ne sont pas stables et donc inaptes aux applications,
bien qu'elles soient d'un grand intérêt fondamental pour la compréhension
de certains mécanismes particuliers de déplacement des électrons
de conduction. Phénoménologiquement, il est assez intuitif que
plus l'épaisseur sera importante et plus le matériau aura un comportement
proche du massif, et à l'inverse plus l'épaisseur sera réduite
et plus le caractère bidimensionnel sera marqué, c'est à
dire plus les surfaces limites interviendront dans les propriétés
physiques. C'est donc cette catégorie de couche ni trop mince ni trop
épaisse (<400 nm) qui va nous intéresser.
Le rapprochement des 2 surfaces, parallèles au plan du substrat, va se
traduire par une contribution accrue de celles-ci aux phénomènes
de dispersion des électrons se déplaçant sous l'effet d'un
champ électrique.
Reprenons le modèle de Mathiessen qui nous a permis d'expliquer la résistivité
d'un matériau massif comme étant la somme de deux termes, l'un
invariant rr directement lié à la structure (ou plutôt
à ses imperfections) c'est-à dire aux surfaces de séparation
des cristaux et l'autre ri dépendant de la température
et fonction du volume interne du cristal. Il va de soi que, si l'on savait construire
un monocristal parfait, la résistivité serait minimale
puisque le terme lié aux défauts disparaitrait. A l'inverse, si
l'on crée une structure extraordinairement désordonnée
sa résistivité va être accrue. Lorsqu'on fabrique une couche
mince c'est le désordre qui va prévaloir. En effet, ainsi qu'on
l'a vu par ailleurs, une couche mince est constituée par dépôt
d'atomes isolés sur un substrat généralement plan. Les
premiers atomes qui vont se déposer sur le substrat vierge vont immédiatement
se condenser puisque celui-ci est à une température où
le matériau constitutif de la couche est normalement à l'état
solide. On va ainsi avoir immédiatement pratiquement autant de
cristaux en puissance que d'atomes déposés. La seconde couche
atomique va conforter ces cristaux initiaux et l'on comprendra aisément
que la couche mince au fur et a mesure de son élaboration va donc être
constituée de très nombreux petits cristaux qui vont tous croître
perpendiculairement au plan du substrat, mais auront dans le plan de celui-ci
des orientations diverses. Une fois le dépôt terminé on
disposera donc d'une couche mince constituée d'une juxtaposition de cristaux
ayant tous la même épaisseur sensiblement, avec comme limite inférieure
et supérieure le substrat, d'une part, et la surface supérieure
de la couche, d'autre part, et qui seront entourés d'un mur vertical
absolument perpendiculaire au plan du substrat et constitué par les limites
des cristaux voisins. La structure obtenue est donc sensiblement différente
de celle d'un matériau massif obtenu par refroidissement d'un liquide
et la taille des cristaux beaucoup plus petite.
 Le rapport surface/volume
des cristaux sera plus important dans la couche obtenue que dans le
matériau massif, ce qui se traduit par un terme rr plus important
dans la couche que dans le massif, tandis que le terme ri est sensiblement
identique dans les deux cas. Lorsqu'on va augmenter l'épaisseur de la
couche, ce ratio va diminuer pour tendre vers une limite qui sera celle du massif.
On voit donc que l'électron de conduction aura plus de surfaces (joints
de grain) à traverser, plus de probabilité de rencontrer les surfaces
limites du cristal que dans le massif ce qui se traduit par une distance parcourue
entre deux collisions (libre parcours moyen) réduite par rapport au matériau
massif et donc une plus grande difficulté à se déplacer
(soit une résistivité accrue).
Le rapport surface/volume
des cristaux sera plus important dans la couche obtenue que dans le
matériau massif, ce qui se traduit par un terme rr plus important
dans la couche que dans le massif, tandis que le terme ri est sensiblement
identique dans les deux cas. Lorsqu'on va augmenter l'épaisseur de la
couche, ce ratio va diminuer pour tendre vers une limite qui sera celle du massif.
On voit donc que l'électron de conduction aura plus de surfaces (joints
de grain) à traverser, plus de probabilité de rencontrer les surfaces
limites du cristal que dans le massif ce qui se traduit par une distance parcourue
entre deux collisions (libre parcours moyen) réduite par rapport au matériau
massif et donc une plus grande difficulté à se déplacer
(soit une résistivité accrue).
De même si l'on examine le coefficient de température de la résistivité
il va être différent pour la couche mince et être sensiblement
réduit (puisque le terme rr est sensiblement plus grand que
dans le massif) et varier avec l'épaisseur. Illustrons cela sur un exemple
pédagogique. Supposons une couche constituée de cristaux de forme
carrée de 1µm2 de surface et de 10nm d'épaisseur.
La surface des joints de grain sera donc de 0.04µm2 soit 4%
de la surface totale. Imaginons que l'on double l'épaisseur de ladite
couche. Le volume d'un cristal va doubler mais la surface limite dudit cristal
ne va varier que de 4%. On voit bien que le déplacement de l'électron
à l'intérieur du cristal ne changera pas mais qu'il aura une moindre
probabilité de rencontrer une des deux surfaces limites. Donc le terme
résistif lié aux surfaces (le terme rr) va diminuer
quand l'épaisseur augmente et simultanément l'importance relative
du terme ri lié à la température va augmenter,
c'est à dire que le terme dr/dq va augmenter
et en conséquence le coefficient de température de la résistivité
doit lui aussi augmenter avec l'épaisseur jusqu'à atteindre la
valeur du massif pour des épaisseurs de l'ordre du µm (mais c'est
très variable car cela dépend de nombreux facteurs dont en premier
lieu la taille moyenne des cristaux).
En pratique après fabrication d'une couche mince on lui fera souvent
subir un traitement thermique afin de favoriser la réorganisation des
cristaux, c'est à dire l'absorption des petits cristaux par leur voisin
plus grand jusqu'à obtenir un état d'équilibre stable et
une résistivité plus faible assez caractéristique de la
température de traitement atteinte.
Nous allons maintenant mettre en équation ce processus.
 Deux cas sont possibles,
Deux cas sont possibles,
- ou la réflexion d'un électron par
la surface limite est spéculaire, c'est à
dire sans perte d'énergie (et la surface se comporte alors comme
un miroir vis à vis d'un rayon lumineux),
- ou bien l'on est en présence d'une dispersion
diffuse avec changement de direction imprévisible
et perte plus ou moins importante d'énergie.
En pratique on constate que les deux mécanismes cohabitent fréquemment
et les travaux de recherche sur les couches minces ont souvent eu pour finalité
de préciser la proportion de réflexion totalement diffuse par
rapport à la réflexion spéculaire dans un matériau
donné et pour des conditions de préparation définies.
Notons que cette façon de traiter le problème est restrictive
car il n'y a pas deux types d'électrons, les uns subissant des réflexions
totalement spéculaires et d'autres totalement diffuses, mais en un point
donné de la surface selon l'incidence et la vitesse de l'électron,
d'une part et la situation instantanée des autres porteurs de charge
mobiles dans son voisinage, d'autre part, un électron subira une réflexion
spéculaire ou plus ou moins diffuse.
 Cependant ce
modèle simplificateur, déjà mathématiquement complexe,
va nous permettre de représenter macroscopiquement
notre couche mince et donc de prévoir à
partir de résultats expérimentaux sur des couches étudiées,
quel serait le comportement d'une couche d'épaisseur différente
et non étudiée.
Cependant ce
modèle simplificateur, déjà mathématiquement complexe,
va nous permettre de représenter macroscopiquement
notre couche mince et donc de prévoir à
partir de résultats expérimentaux sur des couches étudiées,
quel serait le comportement d'une couche d'épaisseur différente
et non étudiée.
La grandeur qui semble bien caractériser cet effet des surfaces c'est
le lpm (libre parcours moyen) des électrons
de conduction. Rappelons que dans le matériau massif la conductivité
s'exprime par s = ne2 lm
/ mv , où n est le nombre d'électrons par unité
de volume, lm leur lpm, v leur vitesse moyenne au voisinage de la
surface de Fermi (n'oublions pas que ce sont les électrons proches du
niveau de Fermi qui sont statistiquement les plus importants pour les phénomènes
de transport).
théorie de Fuchs
Fuchs
en 1936, Sondheimer
et Chambers
en 1952 ont élaboré le modèle de référence.
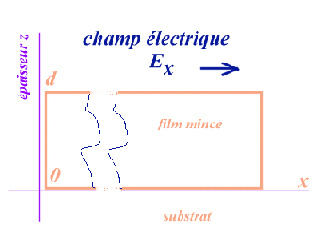
Considérons un film mince soumis à un champ électrique
E dans le sens de sa longueur (selon l'axe des x). On admet que le film est
d'épaisseur uniforme et de structure équivalente au matériau
massif et que sa température est constante.
L'équation de Boltzmann déjà vue s'exprime par
eE/m* df/dvx + vz df/dz = - (f -f0)/
t
le premier terme du premier membre correspond à l'action du champ, le
second fait intervenir le mouvement des électrons situés à
une certaine altitude comprise entre z = 0 (substrat) et z = d (surface supérieure).
f est de la forme f0(vx,vy,vz) +
f1(z,vx,vy,vz) où f0
est la fonction de Fermi-Dirac à l'équilibre en l'absence de champ.
Il vient
df/dvx = df0/dvx + df1/dvx
En première approximation le terme df1/dvx peut
être négligé puisque le champ E est selon x (et donc vx)
De même df/dz = df0/dz + df1/dz peut se simplifier
puisque f0 ne dépend pas de z, il vient donc
df1/dz + f1/tvz = -eE/m*vz
df0/dvx
Cette équation différentielle s'intègre aisément
, sa solution générale est du type:
f1 = - (eEt/m*) df0/dvx
{1+f(vx,vy,vz) exp-z/vz}
La fonction arbitraire f sera déterminée par les conditions
de réflexion des électrons sur les surfaces de la lame mince.
On retient l'hypothèse simplificatrice déjà énoncée,
à savoir qu’une proportion p subit
une réflexion spéculaire (élastique) tandis que 1-p
subit une réflexion totalement diffuse.
Supposons dans un premier temps, ainsi que l'on fait Fuchs et Sondheimer, que
p = 0, c'est à dire que tous les électrons subissent une réflexion
totalement diffuse ce qui revient à considérer que la surface
comporte de nombreux défauts, et c'est souvent réaliste.
Si un électron est réfléchi de façon diffuse à
la surface limite z = 0 cela revient à dire que
sa direction après le choc est indépendante de son angle d'incidence,
elle peut être quelconque dans le 1/2 espace et donc la distribution de
vitesse satisfait à f0.
Il en résulte que la perturbation f1(v,0) pour tous ces électrons
s'éloignant de la surface z = 0 doit être nulle
f1(v,0) = 0 pour tout vz > 0
Le même raisonnement peut être fait pour la surface limite z=d
f1(v,d) = 0 pour tout vz < 0
Si on en revient à l'expression de f1 cela conduit à
f(v) = -1 pour vz> 0 et f(v) = - ed/vz pour vz<
0
et les fonctions de distribution perturbées des électrons sont
respectivement f1+ pour ceux qui s'éloignent de la surface
z = 0 et f1- pour ceux qui quittent la surface z = d
f1+ = - etE/m* df0/dvx {1-e-z/vz}
pour vz>0
f1- = - etE/m* df0/dvx {1 - e(d-z)/vz}
pour vz<0
En utilisant le changement de coordonnées classique on peut écrire
ces expressions en coordonnées polaires, ainsi f1+ devient
f1+ = - etE/m* df0/dv ( 1 - e-z/vcos)
sinqcosy
connaissant la fonction de distribution en fonction de z nous avons alors la
possibilité de calculer la densité de courant. Dans un matériau
massif on avait écrit j =  E,
il en est de même dans la couche mince. Aussi Chambers et Fuchs ont-ils,
après un calcul assez long, exprimé le rapport de la conductivité
E,
il en est de même dans la couche mince. Aussi Chambers et Fuchs ont-ils,
après un calcul assez long, exprimé le rapport de la conductivité
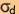 de la couche d'épaisseur d à
la conductivité
de la couche d'épaisseur d à
la conductivité 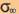 du matériau
massif correspondant.
du matériau
massif correspondant.
Il vient 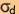 /
/ 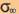 =
= 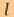 /
/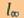 =
F1(
=
F1(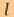 ,p) avec
,p) avec 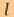 =
d /
=
d /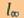 où
où 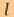 est le libre parcours moyen effectif dans la couche d’épaisseur
d
est le libre parcours moyen effectif dans la couche d’épaisseur
d
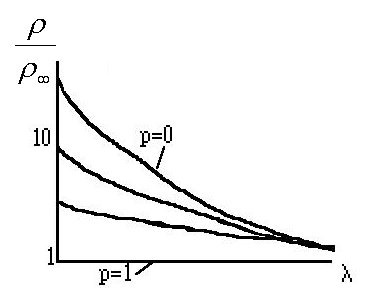
dans cette relation la variable d'intégration t représente la
quantité t = d /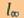 cos
cos =
=
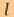 / cos
/ cos .
.
Le graphique ci-dessus donne l'allure des courbes représentatives de
 /
/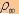 (c'est
à dire l'inverse de
(c'est
à dire l'inverse de 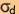 /
/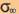 )
en fonction de
)
en fonction de 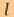 . On notera que
l'horizontale correspond à la valeur 1 du rapport c'est à dire
au cas où p = 1 pour lequel l'effet d'épaisseur est inexistant.
. On notera que
l'horizontale correspond à la valeur 1 du rapport c'est à dire
au cas où p = 1 pour lequel l'effet d'épaisseur est inexistant.
Précisons quelques résultats expérimentaux
obtenus dans des conditions rigoureusement similaires, en ultra vide sur substrat
de verre de silice poli optiquement (thèse
M. HUBIN, Rouen 1972): pour le cuivre on avait obtenu p = 0, pour
l'argent p = 0.16, pour l'or p = 0.6 et ultérieurement (thèse
G. RICHON, Rouen 1977) pour les alliages Cu/Ni p = 1.
Notons que des travaux plus récents ont cherché à améliorer
la correspondance entre les résultats expérimentaux et l'expression
théorique de 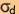 /
/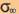 en introduisant des paramètres p1 et p2 différents pour les deux
surfaces, puis en considérant qu'en raison de la faible épaisseur
et du processus de croissance par strate d'une couche mince il y avait lieu
de tenir compte en plus des joints de grain (car les cristaux sont généralement
plus petits dans une couche mince que dans le massif)(Mayadas68), ou de faire
varier p avec l'angle d'incidence (Cotti65). Ces travaux théoriques n'ont
cependant pas apporté sur le plan pratique d'informations notoirement
supérieures à celles déduites des travaux de Fuchs.
en introduisant des paramètres p1 et p2 différents pour les deux
surfaces, puis en considérant qu'en raison de la faible épaisseur
et du processus de croissance par strate d'une couche mince il y avait lieu
de tenir compte en plus des joints de grain (car les cristaux sont généralement
plus petits dans une couche mince que dans le massif)(Mayadas68), ou de faire
varier p avec l'angle d'incidence (Cotti65). Ces travaux théoriques n'ont
cependant pas apporté sur le plan pratique d'informations notoirement
supérieures à celles déduites des travaux de Fuchs.
Par ailleurs Sondheimer a montré que le coefficient de température
de la résistivité  = dR/(R0d
= dR/(R0d )
variait selon une loi semblable qui pouvait se simplifier pour les épaisseurs
élevées (d>
)
variait selon une loi semblable qui pouvait se simplifier pour les épaisseurs
élevées (d>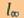 )
)
 d =
d = 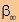 [d-3
[d-3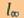 (1-p)/8]
soit encore
(1-p)/8]
soit encore  /
/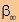 =
1-3(1-p)/8
=
1-3(1-p)/8
Notons encore que l'étude des couches minces peut se révéler
un puissant moyen d'investigation et de connaissance des paramètres du
matériau massif considéré comme couche mince d'épaisseur
infinie en particulier le produit  d
à une température donnée permet de conduire à
d
à une température donnée permet de conduire à 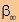 et
et 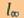
Conséquences pratiques:
 Les principaux enseignements
que l'on peut tirer des travaux de Fuchs et de ses successeurs sont les suivants:
Les principaux enseignements
que l'on peut tirer des travaux de Fuchs et de ses successeurs sont les suivants:
| En règle
générale la résistivité d'une couche
mince sera supérieure à celle du massif et son lpm
inférieur. |
| Le coefficient
de température augmentera avec l'épaisseur pour tendre
vers celui du massif à grande épaisseur. |
| La connaissance
de ces paramètres pour plusieurs épaisseurs, permet
par extrapolation en utilisant les courbes de Fuchs, de prévoir
les valeurs de ces paramètres aux autres épaisseurs
dans la mesure où l'on sait reproduire
la même structure (donc la même valeur de p) quelle que
soit l'épaisseur. |
Il est ainsi possible d'imaginer une géométrie
de dépôt, d'une certaine épaisseur, pour un certain matériau
qui possédera un coefficient de température et une résistivité
précis, parfaitement adaptés à l'application envisagée.
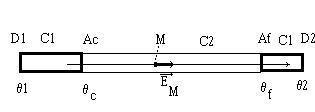
Pouvoir thermoélectrique d'une couche mince
Dans le cas des couches minces, si le conducteur C2 est constitué d'une
couche mince (notée M*) de même matériau que
C1 massif (noté 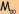 ),
on obtient une f.e.m. d'effet Seebeck
),
on obtient une f.e.m. d'effet Seebeck
intégrale prise entre  C
et
C
et  F et où
(
F et où
( *-
*-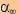 )
=
)
=
 représente le pouvoir thermoélectrique relatif du film par rapport
au massif.
représente le pouvoir thermoélectrique relatif du film par rapport
au massif.
Dans tous les cas on constate une augmentation
algébrique du pouvoir thermoélectrique quand on diminue
l'épaisseur. La raison en est la suivante, dans le matériau
en couche mince les électrons, dont on a vu précédemment
qu'ils sont responsables de deux courants de diffusion de sens opposés
notés Jdiff- et Jdiff+, sont freinés par
les réflexions non spéculaires sur les faces de la couche, mais
ce freinage affecte relativement plus les électrons
les
plus énergétiques responsables de Jdiff-.
Il en résulte donc une augmentation relative de la contribution de Jdiff+
se traduisant par une augmentation algébrique de  *
lorsque l'épaisseur diminue.
*
lorsque l'épaisseur diminue.


Nous donnons ici quelques éléments complémentaires à
l'attention des lecteurs intéressés par la technologie des couches
minces.
[1] Chambers RG, Proc Roy Soc (London) A 202 (1950) 378 et A 215 (1952)
481
[2] Cotti P, Helv Phys Acta 38 (1965) 801
prise en compte de l'angle d'incidence dans la réflexion des électrons
[3]Fuchs K, Proc Cambridge Phil Soc 34 (1938) 100
[4] Hubin M, Thèse réf CNRS AO 7793,
Rouen 1972
propriétés thermoélectriques des films de métaux
nobles
[5] Gouault J, Hubin M, brevet ANVAR ,1975
procédé de contrôle de fabrication d'alliage binaire en
couche mince par coévaporation asservie
[6] Mayadas AF, J Appl Phys, 39 (1968) 4241
prise en compte des joints de grain dans les propriétés de transport
des films minces
[7] Sondheimer EH, Adv Phys, 1 (1952) 1
[8] Richon G, thèse de doctorat , Rouen
1977
alliages Cu/Ni en couches minces
[9] Grigorov G et Kanev V, le Vide poussé, Masson Ed, Paris
(1970) ouvrage de référence
[10] Lempérière G, Le Vide 229 (1985) 549
étude des procédés de sputtering
[11] Pauleau Y, Le Vide 227 (1985) 319
dépôts par laser
[12] Barraud A, le Vide 227 (1985) 359
films de Langmuir-Blodgett
[13] Tholomier M, le Vide 238 (1987) 385
analyse Auger quantitative
[14] Mayer H, Dünne Schichten Technik, Springer Verlag Berlin
(1955).
L'ouvrage de référence sur les propriétés des couches
minces.
[15] Duval P, High vacuum production in the microelectronics industry,
Elsevier Ed, Amsterdam (1988).
L’avant dernier ouvrage publié par le meilleur spécialiste
français. 



En pratique, il sera surtout essentiel de retenir les grandes conséquences que l'on peut en dégager, en ce qui concerne le développement d'applications technologiques des couches minces dans des capteurs de mesures physiques, en gardant constamment à l'esprit qu'il faut toujours être très prudent quand on veut employer des couches minces, car il y a souvent des comportements imprévus mettant en défaut les théories les plus élaborées.
Cependant ce modèle simplificateur, déjà mathématiquement complexe, va nous permettre de représenter macroscopiquement notre couche mince et donc de prévoir à partir de résultats expérimentaux sur des couches étudiées, quel serait le comportement d'une couche d'épaisseur différente et non étudiée.
 E,
il en est de même dans la couche mince. Aussi Chambers et Fuchs ont-ils,
après un calcul assez long, exprimé le rapport de la conductivité
E,
il en est de même dans la couche mince. Aussi Chambers et Fuchs ont-ils,
après un calcul assez long, exprimé le rapport de la conductivité
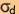 de la couche d'épaisseur d à
la conductivité
de la couche d'épaisseur d à
la conductivité 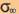 du matériau
massif correspondant.
du matériau
massif correspondant.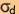 /
/ 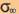 =
= 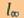 =
F1(
=
F1(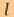 ,p) avec
,p) avec 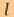 =
d /
=
d /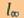 où
où 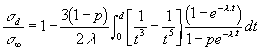
 =
=
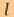 / cos
/ cos .
.
 /
/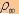 (c'est
à dire l'inverse de
(c'est
à dire l'inverse de 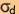 /
/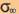 )
en fonction de
)
en fonction de 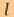 . On notera que
l'horizontale correspond à la valeur 1 du rapport c'est à dire
au cas où p = 1 pour lequel l'effet d'épaisseur est inexistant.
. On notera que
l'horizontale correspond à la valeur 1 du rapport c'est à dire
au cas où p = 1 pour lequel l'effet d'épaisseur est inexistant.
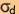 /
/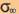 en introduisant des paramètres p1 et p2 différents pour les deux
surfaces, puis en considérant qu'en raison de la faible épaisseur
et du processus de croissance par strate d'une couche mince il y avait lieu
de tenir compte en plus des joints de grain (car les cristaux sont généralement
plus petits dans une couche mince que dans le massif)(Mayadas68), ou de faire
varier p avec l'angle d'incidence (Cotti65). Ces travaux théoriques n'ont
cependant pas apporté sur le plan pratique d'informations notoirement
supérieures à celles déduites des travaux de Fuchs.
en introduisant des paramètres p1 et p2 différents pour les deux
surfaces, puis en considérant qu'en raison de la faible épaisseur
et du processus de croissance par strate d'une couche mince il y avait lieu
de tenir compte en plus des joints de grain (car les cristaux sont généralement
plus petits dans une couche mince que dans le massif)(Mayadas68), ou de faire
varier p avec l'angle d'incidence (Cotti65). Ces travaux théoriques n'ont
cependant pas apporté sur le plan pratique d'informations notoirement
supérieures à celles déduites des travaux de Fuchs. = dR/(R0d
= dR/(R0d )
variait selon une loi semblable qui pouvait se simplifier pour les épaisseurs
élevées (d>
)
variait selon une loi semblable qui pouvait se simplifier pour les épaisseurs
élevées (d>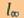 )
)
d =
[d-3
(1-p)/8] soit encore
/
= 1-3(1-p)/8
 d
à une température donnée permet de conduire à
d
à une température donnée permet de conduire à 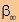 et
et 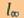
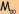 ),
on obtient une f.e.m. d'effet Seebeck
),
on obtient une f.e.m. d'effet Seebeck C
et
C
et  F et où
(
F et où
( *-
*-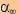 )
=
)
=
 représente le pouvoir thermoélectrique relatif du film par rapport
au massif.
représente le pouvoir thermoélectrique relatif du film par rapport
au massif. *
lorsque l'épaisseur diminue.
*
lorsque l'épaisseur diminue.
