phenomenologie

Dans ce chapitre on va, sans calcul, examiner quelques effets perturbateurs sur le solide, effets sur lesquels on reviendra ultérieurement, en particulier dans les chapitres consacrés aux capteurs.
considérations structurales

Dans le chapitre précédent, on a considéré un solide supposé parfait. La réalité est souvent différente en raison des nombreux défauts dans la structure, consécutifs au mode de préparation du solide. Le plus souvent un matériau métallique est obtenu selon un processus métallurgique qui passe par une étape à haute température dans laquelle le métal est à l'état liquide, suivie d'une étape de refroidissement au cours de laquelle le matériau passe à l'état solide.
En pratique, au cours de cette phase de refroidissement, on va d'abord constater qu'en un point juste un peu plus froid deux atomes puis trois, puis quatre, etc. vont se figer en s'agglomérant les uns aux autres, c'est à dire en formant l'amorce d'un monocristal parfait. La direction dans laquelle se produit cette cristallisation est le plus souvent aléatoire, en fait elle résulte très précisément de la position relative au début du processus des deux premiers atomes qui vont s'associer. Les autres atomes devront continuer le cristal en respectant l'axe originel d'où découleront les autres.
Cependant, à un autre endroit du liquide, il est tout a fait vraisemblable que le même processus s'est initié et qu'un second cristal est en cours de formation. Il n'y a aucune raison qu'il possède une direction privilégiée identique à celle du premier cristal. D'autres vont aussi apparaître et croître au fur et à mesure du refroidissement.

A un certain moment il est certain que deux cristaux en pleine expansion vont se rencontrer et il est fort probable que leurs directions étant différentes la frontière entre eux sera réelle (et visible au microscope) et se traduira par une discontinuité.

On peut rencontrer plusieurs types de discontinuité : soit un atome va se retrouver coincé entre les deux cristaux et assurera une espèce de lien sans qu'on puisse affirmer qu'il appartient à un cristal ou à l'autre parce qu'il sera "distordu" dans une position intermédiaire on parle d'atome intersticiel, soit un espace trop important entre les deux cristaux subsiste sans qu'un atome ne puisse s'y glisser et on a alors une lacune. Cette lacune peut se prolonger sur plusieurs distances atomiques. Dans les deux cas on aura entre les deux cristaux, les deux grains, un "joint" qu'on appellera joint de grains, c'est à dire une discontinuité structurale permettant de passer d'un cristal à l'autre. Il va de soi que la manière dont s'effectue le refroidissement va jouer un grand rôle dans la cristallisation et l'obtention de plus ou moins nombreux joints de grain.

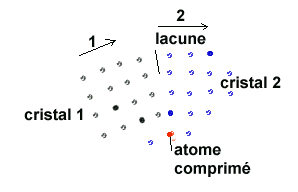
Quel sera l'effet de ces cristaux d'orientation différente sur les propriétés physiques du matériau. On conçoit aisément que plus les cristaux seront petits, et donc les discontinuités nombreuses et moins le matériau sera dense. La densité d'un matériau n'est donc pas aussi constante que ne pourraient le laisser croire les tables de constante. En fait cela joue très peu et on considère cet effet sur la densité comme négligeable. Mais si l'on mesure la densité d'un morceau de cuivre normalement cristallisé et du même morceau écroui, c'est à dire soumis à un martellement intense qui aura comme conséquence de multiplier très fortement les lacunes, on met aisément en évidence une différence de densité.

impact sur les propriétés électriques

Par contre l'effet de cette microcristallisation sera notable sur l'ensemble des propriétés électriques, magnétiques et optiques. Prenons, à titre d'exemple, la résistivité dont on sait qu'elle caractérise la résistance au déplacement des électrons dits de conduction, c'est à dire ceux dont l'énergie est telle qu'ils peuvent aisément se déplacer de proche en proche d'un atome à un autre.

Lorsqu'un tel électron se déplace à l'intérieur d'un monocristal, il est soumis à un champ électrique qui varie périodiquement puisqu'il y a une périodicité dans l'espace du positionnement des noyaux, mais lorsqu'il va atteindre la frontière entre deux cristaux il va subir une perturbation locale puisque, localement, selon qu'il y a un atome un peu "compressé" ou au contraire absent, le champ résultant sera différent. On comprend aisément que plus les cristaux seront petits et plus les perturbations seront importantes. On caractérise cela par la relation dite de Matthiessen qui annonce que la résistivité d'un matériau est la somme de deux termes : l'un caractérisant le cristal parfait et l'autre les défauts. Loi qui prédit que le terme caractérisant le cristal parfait

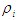varie avec la température quelle que soit celle-ci, tandis que celui lié aux défauts de structure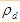

est invariant tant que ceux-ci n'évoluent pas, c'est à dire jusqu'à une certaine température dépassant le plus souvent plusieurs centaines de degrés Celsius.

En effet, à partir d'une certaine température l'agitation des noyaux est telle qu'il en résulte une possibilité pour un atome de quasiment changer d'orientation. En clair cela veut dire qu'un atome faisant partie d'un cristal pourra évoluer et se raccorder à un autre, cela ne va évidemment affecter que les atomes en limite d'un cristal et l'expérience montre que ce processus de "diffusion" va profiter toujours aux plus gros cristaux au détriment des plus petits qui vont disparaitre. Ainsi un traitement thermique judicieux permettra de transformer un polycristal progressivement en un quasi-monocristal, c'est un procédé que l'on exploitera fréquemment avec divers moyens technologiques.

incidence d'une déformation mécanique

Examinons ce qui se passe dans un groupe d'atomes au coeur d'un solide soumis à une déformation que l'on qualifiera de réversible. Par exemple un allongement. Plaçons nous à l'intérieur d'un cristal. La traction que l'on va faire subir au matériau va induire un allongement macroscopique que l'on peut éventuellement voir à l'oeil nu. Au niveau du groupe d'atomes témoin cela va se traduire par une augmentation de la composante de distance entre noyaux, colinéaire avec la direction de la traction. Il est aussi évident que cette augmentation n'affectera pas l'équilibre entre ces atomes voisins de la même façon si la direction de traction se trouve être confondue avec l'axe du cristal ou si elle est quelconque.

l'incidence de la traction sur la trajectoire de l'électron est différente en zone 1 et zone 2

Mais dans tous les cas l'allongement va se traduire par un allongement des distances que devra franchir un électron de conduction pour aller d'un point à un autre et donc une augmentation de son trajet et de son temps de trajet, ce qu'on traduit par un accroissement de résistivité. La mesure de la résistivité va donc être significative de la déformation et ce sera un procédé très employé dans les capteurs.

Bien évidemment ce processus d'allongement possède une certaine réversibilité, mais lorsqu'on exercera une traction trop forte on constatera une rupture de l'échantillon soumis à la traction. En fait lorsqu'on va exercer une traction croissante on va constater que les forces en jeu vont agir préférentiellement sur les points faibles de la structure, c'est à dire au niveau des joints de grain et des lacunes. Celles-ci vont avoir tendance à s'accroitre bien plus vite que les distances interatomiques et très vite l'élargissement des lacunes va devenir d'abord irréversible (limite dite d'élasticité) puis conduire à la rupture. Si l'on examine plusieurs éprouvettes du même métal, supposées identiques a priori, soumises au même processus de traction on va donc constater : d'une part, que l'effort aboutissant à la rupture n'est pas exactement le même et, d'autre part, qu'après rupture les frontières de rupture sont différentes ce qui traduit qu'à l'échelle microscopique deux échantillons sont différents dans leur répartition lacunaire.

La conséquence que l'on peut tirer de cette expérience c'est que l'analyse des contraintes réalisée à partir de mesures de variation de résistivité d'un matériau est possible, mais qu'il ne faut pas en attendre des résultats d'une trop grande précision si le matériau dont est constitué le capteur de déformation ne peut être reproduit lui-même avec une très grande précision à l'échelle microscopique (ce qui est le plus souvent le cas).

La seconde conséquence c'est, que d'un échantillon à un autre, la charge de rupture pouvant donc différer, dans toutes les applications où l'on aura un métal (et tout particulièrement un cable métallique) soumis régulièrement (ou de manière permanente) à une tension on devra prendre un coefficient de sécurité pour tenir compte du cas où le cable serait un échantillon comportant en un endroit un point de rupture plus faible que la moyenne. Ainsi le cable d'un téléphérique sera-t-il nécessairement surdimensionné. Cependant la permanence des tensions va induire un phénomène lent mais inexorable de migration et élargissement des lacunes qui conduira obligatoirement après un temps indéterminé à la rupture soudaine du cable au moment du passage de la cabine, c'est à dire d'une surcharge temporaire. Comme il est très difficile d'examiner finement l'évolution structurelle du cable installé, en fonction du temps, il est parfaitement prévisible qu'un risque d'accident va s'accroître au cours du temps sans qu'on puisse le prévoir avec précision.

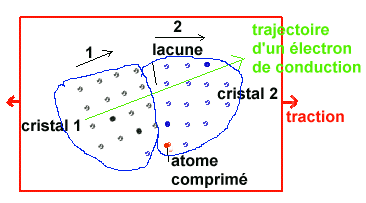
Effet de la température sur la trajectoire d'un électron libre

Malheureusement d'autres grandeurs jouent aussi sur la résistivité et, en particulier, la température. Quand celle-ci va augmenter on va constater plusieurs conséquences contradictoires : l'énergie des électrons libres va augmenter, ce qui revient à dire que leur vitesse aurait tendance à croître ce qui militerait pour une réduction des temps de parcours et donc une décroissance apparente de la résistivité. En fait deux autres éléments vont contrarier cette vitesse accrue. D'une part, le risque pour un électron d'en percuter un autre semble accru (cf automobiles!) et, d'autre part, l'oscillation des noyaux autour de leur position moyenne s'amplifie avec la température ce qui revient à dire que la trajectoire des électrons entre ces noyaux va elle même être perturbée: en première approximation on peut dire que l'espace libre pour le passage de l'électron est réduit, ce qui revient à dire qu'il va s'approcher plus des noyaux dont la charge positive va lui faire subir une déviation plus forte et donc globalement le ralentir.

graphique illustrant l'influence de la température: à gauche à très basse température les noyaux oscillent très peu autour de leur position d'équilibre, leur influence sur l'électron est symétrique et sa trajectoire reste linéaire, à droite à très haute température ils oscillent beaucoup (on a figuré en rouge l'enveloppe de leur limite oscillatoire et en noir les positions respectives des noyaux à un instant figé). L'électron se déplaçant le long de la flèche (par exemple) sera beaucoup plus influencé par les noyaux à haute température qui pourront être beaucoup plus près à un instant donné (rappelons que dans la loi de Coulomb c'est l'inverse du carré de la distance qui joue: ainsi dans la figure de droite le noyau en A va avoir une influence fortement accrue par rapport au cas de gauche tandis que le noyau B aura une action réduite, à l'instant immortalisé par la figure bien évidemment, le résultat est un allongement de la trajectoire tel celui figuré à titre d'exemple).

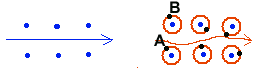
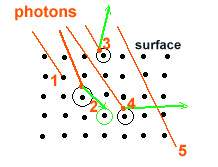
action d'un rayonnement électromagnétique

Lorsqu'un matériau est sous l'effet d'un rayonnement, selon l'énergie de celui-ci divers effets peuvent se produire. Un photon incident va pénétrer dans le matériau jusqu'à ce qu'il rencontre une particule constitutive de celui-ci c'est à dire un électron ou un nucléon.

Comme nous avons montré que la matière est très vide il se peut que le photon traverse l'ensemble de l'échantillon de matériau et ne provoque alors aucune conséquence.

Il peut heurter un nucléon ce qui eu égard à leur dimension est de très faible probabilité, dans ce cas son énergie sera cédée au nucléon et globalement on aura donc une augmentation de température. Cet effet est d'autant plus important que le nombre de photons, donc l'intensité du rayonnement, est important (cela explique en partie le fait que l'énergie solaire tombant sur une ardoise va induire un réchauffement de celle-ci).

A cet effet thermique toujours présent va s'ajouter l'effet des photons heurtant un électron. Plusieurs cas sont alors possibles selon l'intensité de l'énergie du photon et selon le niveau d'énergie de l'électron heurté. L'électron peut ainsi être catapulté à l'extérieur du matériau (effet photoélectrique externe), il peut changer de niveau d'énergie et de bande d'énergie ou rester dans la même bande d'énergie mais avec un niveau supérieur. Ainsi le photon peut amener un électron de valence dans la bande de conduction et induire donc une augmentation du courant (ou si l'on préfère une diminution de la résistivité), mais il peut simplement induire une accélération d'un électron qui était déjà dans la bande de conduction ce qui simule ce qui se passe lorsque la température augmente.

On a donc des effets assez contradictoires, mais il faut en outre remarquer que l'endroit où le photon heurte un électron va aussi jouer un rôle dans le résultat. En effet si un électron est éjecté de son atome et qu'il s'agit d'un atome proche de la surface il y a une certaine probabilité pour qu'il se dirige en dehors du métal. Et si sa vitesse (donc l'énergie qu'il a récupéré) est suffisante il va effectivement en sortir et donc être perdu pour le matériau. Par contre, s'il s'agit d'un électron au coeur du matériau, il sera soumis aux actions électrostatiques des autres noyaux, au risque de percussion d'un autre électron et il y a fort à parier qu'il finira par "rentrer dans le rang" et que l'énergie du photon sera alors, in fine, transformée en chaleur.

fig: illustration de cinq cas possibles. En 1 le photon rencontre un noyau, en 2 il percute un électron mais avec insuffisamment d'énergie et l'électron va être repris par l'atome voisin qui disposait d'une place libre, en 3 l'électron d'un atome de surface est éjecté vers l'extérieur, en 4 un électron est passé d'une bande de valence à une bande de conduction et participe donc à celle-ci enfin en 5 le photon a traversé tout le matériau sans rencontrer d'obstacle.

On constate donc qu'on va pouvoir exploiter ces différents effets en essayant par une structure judicieuse de privilégier l'un d'entre eux plutôt que les autres et on aura ainsi la possibilité d'imaginer des capteurs intéressants. Avec un matériau sous forme de couche très mince on va privilégier l'effet thermoélectrique et l'exploiter pour mesurer l'intensité du rayonnement, un capteur massif exploitera plutôt l'effet thermique, enfin en choisissant astucieusement le matériau on pourra sélectionner une certaine longueur d'onde seule capable de faire passer un électron de la bande de valence à la bande de conduction supérieure et donc identifier certaine source spécifique de ce rayonnement (ex. rayonnement nucléaire), etc.

	Copyright © 2000-2015 LHERBAUDIERE	6 pages à l'impression			version initiale 2002
	AVERTISSEMENT				dernière mise à jour 18 mars 2013

considérations structurales	l'association de cristaux
déformations	les conséquences
perturbations thermiques	idem
absorption d'un rayonnement	idem
		une collection d'icônes pour visiter tout le site