Copyright
© 2000-2015 LHERBAUDIERE


2 pages à l'impression		 version initiale 2002
AVERTISSEMENT dernière mise à jour
17 mai 2013
cliquez sur le mot avertissement ou information ci-dessus pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives

PHYSIQUE DU SOLIDE
partie 5/7 conductibilité du semiconducteur

semiconducteur intrinsèque un matériau parfait
mouvement des électrons la notion de mobilité
conductibilité du cristal la densité de courant
semiconducteur extrinsèque le matériau dopé
une collection d'icônes pour visiter tout le site

semiconducteur intrinsèque

Un semiconducteur dit intrinsèque est un matériau idéal ne possédant ni défaut physique ni défaut chimique. Un tel monocristal possède une structure de type tétraédrique (la pyramide du Louvre représente une telle structure) c'est à dire que chaque atome est entouré symétriquement de 4 atomes. Cette structure tridimensionnelle ne se prêtant pas à une représentation aisée on représente, conventionnellement, cet arrangement à l'aide d'un modèle plan pour expliquer les propriétés.


Fig. représentation planaire du semiconducteur et notion de trou

Dans un semi conducteur la bande interdite, séparant la bande de valence et la bande de conduction, va jouer un rôle important.

matériau Si Ge GaAs GaP PbTe
largeur de la bande interdite (eV) à 300K 1.1 0.7 1.4 2.25 0.3

A 0K tous les électrons sont dans la bande de valence Bv; à T > 0K certains ayant une énergie > Ec se libèrent et passent dans la bande de conduction Bc. Tout atome ayant perdu un électron devient un ion positif qui va aisément capturer un électron d'un atome voisin lorsqu'il passera dans l'espace commun aux deux atomes et l'on constate donc un déplacement apparent du manque d'électron. Par abus de langage on dit : que le trou équivalent à une charge mobile +q se déplace dans la bande de valence.

La concentration en électrons se déduit de la connaissance de la densité d'états et de la probabilité d'occupation.
avec dans l'expression de n, le terme précédant l'exponentielle est appelé concentration effective (des places de niveau Ec) et vaut environ
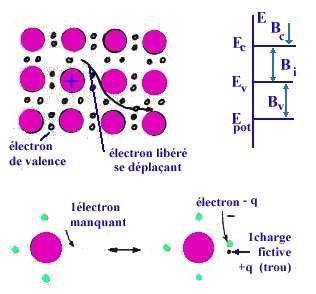
De même qu'on a pu déterminer une masse effective me de l'électron dans le semiconducteur, on peut définir une masse effective mh des trous dans la bande de valence. Notons que, par nécessité, il y a dans un semiconducteur intrinsèque autant de trous dans la bande de valence que d'électrons dans la bande de conduction, ainsi si l'on appelle p la concentration en trous on aura n = p. Et en faisant le même raisonnement pour les trous que pour les électrons on peut montrer que

on en déduit

or n = p et l'on écrit np = ni2 en appelant conductivité intrinsèque la quantité en posant Eg = Ec-Ev largeur de la bande interdite.

A partir des expressions de n et de p on peut en tirer le niveau de Fermi
Aux températures usuelles la quantité kT est petite et le second terme peut-être négligé en première approximation et le niveau de Fermi se trouve donc au milieu de la bande interdite.

Autre remarque : en examinant l'expression de ni on voit que le terme entre crochets, variant en T puissance 3/2, varie peu vis à vis du terme exponentiel, donc la conductivité d'un semiconducteur intrinsèque varie sensiblement comme une exponentielle en -1/T ce qui différencie sensiblement les semiconducteurs des métaux lesquels voient leur résistivité varier sensiblement proportionnellement à T. Cependant si la température vient à croître fortement (plusieurs centaines de °C) le terme en T3/2 va finir par varier plus vite que le terme exponentiel et le semiconducteur verra alors une variation de sa résistivité de type métallique ce qui ne présentera plus d'intérêt pratique : les semiconducteurs ne pourront donc être exploités qu'à des températures proches de l'ambiante, dès lors qu'ils seront traversés par des courants importants, générant un effet Joule conséquent, on sera donc contraint de les refroidir pour limiter leur température à des valeurs acceptables pour lesquelles leurs propriétés restent convenables. Cette contrainte explique la présence de radiateurs et de ventilateurs dans nombre de dispositifs à semiconducteurs.

mouvement des électrons

A une température T quelconque un électron libre possède une vitesse dite thermique telle que soit sensiblement 100km/s à 300K.

On constate que cet électron se déplace suivant une trajectoire que nous assimilerons à une succession de segments de droite (en raison des perturbations multiples dues aux défauts ponctuels, chimique, de structure, aux rencontres avec des trous...). 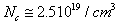Les porteurs ont donc une durée moyenne de vie (limitée par le processus de recombinaison électron-trou), un parcours moyen entre 2 collisions relié à vth par dans lequel est le temps de relaxation ou durée moyenne de parcours (environ 0.75 ps pour le silicium).

Essayons d'exprimer ce mouvement d'un électron en présence d'un champ électrique E selon la direction x et supposons qu'à l'instant t = 0 l'électron vient de subir une collision et qu'il a une composante de vitesse v0 selon x.

A l'instant t cette vitesse résultant de la force f = -qE = mdv/dt devient donc

or un simple raisonnement nous montre, puisqu'à chaque collision la direction de l'électron changera, que la composante moyenne selon x doit être nulle et donc la vitesse moyenne de l'électron sera la quantité µn est appelée mobilité des électrons. Un raisonnement semblable conduit à la mobilité des trous µp.

température 300K Si Ge
ni /cm3 1.5.1010 2.5.1013
µn cm2/V.s 1350 3900
µp cm2/V.s 480 1900
ri = 1/si W.cm 2.105 47

conductibilité du cristal

En ne considérant que la vitesse d'entraînement des électrons à travers une surface dS perpendiculaire au champ E, la charge transportée est . On a une expression analogue pour les trous et la densité totale de courant est donc où représente la conductivité du matériau.

semiconducteur extrinsèque

En ajoutant dans un semiconducteur intrinsèque une faible proportion de "dopant" (seulement 1 atome pour 108 atomes de semiconducteur) constitué soit d'un atome trivalent B Al Ga In ou pentavalent P As Bi Sb on obtient un semiconducteur extrinsèque.

Prenons le cas d'un pentavalent en position de substitution, il met 4 électrons en commun avec ses 4 plus proches voisins et son cinquième électron est peu lié. On peut montrer que son énergie de liaison est effectivement de 0.048eV dans une matrice de Si et de 0.027eV dans le Ge. C'est ce peu d'énergie qu'il suffit de lui fournir pour le libérer. Cela revient à dire que sur le diagramme énergétique du semiconducteur, son niveau d'énergie se place très près du bas de la bande de conduction (à 0.047eV pour le Si) mais dans la bande interdite. Si on a une concentration Nd en atomes pentavalents (ou donneurs d'électron) on aura donc Nd niveaux très voisins de 0.05eV au dessous de Ec. Nd étant faible par hypothèse, la distance entre deux atomes d'additif est suffisamment importante pour que l'on admette que le principe de Pauli ne joue pas entre ces atomes et que le niveau n'est donc pas élargi.

Conséquence pratique: Prenons l'exemple du silicium à l'ambiante, on a, selon le tableau ci-dessus, ni = 1.51010/cm3 ce qui revient à dire que l'on a la même quantité d'électrons libérés dans le matériau intrinsèque. Or à 300K on a kT = 0.25eV environ ce qui est >>0.048eV. Il en résulte que tous les atomes de dopant du simple fait de la température auront perdu leur cinquième électron périphérique. Il suffit donc que Nd soit 105 fois supérieur à ni pour que la conductivité du matériau soit accrue d'un facteur 100000. Un simple calcul montre que cela correspond à environ 1 atome de donneur pour 1 milliard d'atomes de silicium. On en conclut évidemment que dans un semiconducteur intrinsèque la conductivité va dépendre quasi exclusivement de la concentration d'atomes dopants. L'autre conclusion c'est qu'on dispose maintenant d'un matériau dans lequel le nombre d'électrons libres est bien supérieur à celui des trous (dont la plupart vont d'ailleurs être recombinés).

Si l'impureté comporte seulement 3 électrons de valence (atome accepteur d'électron) c'est le processus inverse qui se produit. L'additif récupère volontiers un électron supplémentaire ce qui crée un trou peu lié supplémentaire (de niveau énergétique juste supérieur au niveau du haut de la bande de valence du semiconducteur) et, si Na est sa concentration, le même raisonnement montre que la conductibilité du cristal est alors due essentiellement aux trous.

Un calcul permet dans le cas du semiconducteur extrinsèque de calculer la modification apportée au niveau de Fermi par l'additif. On montre ainsi que pour un semiconducteur de type N (donc dopé avec une concentration Nd d'atomes pentavalents) c'est à dire que le niveau de Fermi se trouve proche du bas de la bande de conduction et non plus au milieu de la bande interdite. Dans le cas d'un matériau dopé P le niveau de Fermi se trouverait au contraire diminué et proche du haut de la bande de valence selon la relation . Dans les deux cas on voit qu'une augmentation de température tendra à ramener le niveau au milieu de la bande interdite, transformant alors le matériau en matériau intrinsèque. La limite de température est évidemment théoriquement augmentée avec la valeur de Na ou Nd mais d'autres contraintes interdisent un dopage élevé pour les applications et par conséquent la limite d'emploi en température des semiconducteurs restera modeste.

Une autre remarque : la mobilité du matériau extrinsèque, tant pour les trous que pour les électrons, est diminuée dès lors que la concentration en atomes de dopant devient notable. La figure ci-dessous montre cet effet et justifie la nécessité de ne pas trop doper le matériau. L'explication est simple, l'atome dopant est ionisé, c'est à dire qu'il possède une charge active de signe opposé à celle du porteur libre, tant que le nombre d'atomes dopant est très faible ces porteurs ont une grande probabilité dans leur déplacement de passer suffisamment loin pour que le champ attractif de l'ion ne les dérange pas, mais dès lors que ce nombre d'ions atteint une densité significative ils vont gèner significativement le déplacement des porteurs libres et donc induire une réduction du lpm et donc de la mobilité ce qui n'est pas favorable pour les applications (ça revient à limiter la fréquence de fonctionnement des dispositifs).


Fig. évolution de la mobilité en fonction de la concentration de dopant

 Hit-Parade