
Copyright
© 2000-2015
LHERBAUDIERE
2 pages à l'impression

17 mars 2013
 |
Copyright |
2 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 17 mars 2013 |
PHYSIQUE DU SOLIDE
partie 6/7 équation de continuité
et jonctions
| phénomène de diffusion | la première loi de Fick | |||
| équation de continuité | la seconde loi de Fick | |||
| application | la longueur de diffusion | |||
| jonction métal-métal | retrouvons la ddp de Volta | |||
| jonction métal-semiconducteur | comment faire une diode Schottky | |||
une
collection d'icônes pour visiter tout le site |
||||
 n
et p = p0 +
n
et p = p0 +  p
avec
p
avec  n =
n =  p
dans la zone éclairée (voir fig.).
p
dans la zone éclairée (voir fig.).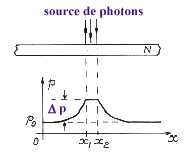
| en cm2/s | Ge | Si |
| Dp | 44 | 6.5 |
| Dn | 93 | 31 |
 t,
on admet qu'il ne se produit aucune recombinaison ni création de paire
électron-trou, la quantité [Fp(x) - Fp(x+dx)]
t,
on admet qu'il ne se produit aucune recombinaison ni création de paire
électron-trou, la quantité [Fp(x) - Fp(x+dx)] t
=
t
=  P représente l'acroissement
du nombre de trous pendant ce temps dans le volume limité par les deux
plans auquel correspond une augmentation Dp de leur concentration définie
par
P représente l'acroissement
du nombre de trous pendant ce temps dans le volume limité par les deux
plans auquel correspond une augmentation Dp de leur concentration définie
par  P/
P/ x
soit Dp = [Fp(x) - Fp(x+dx)]
x
soit Dp = [Fp(x) - Fp(x+dx)] t
/
t
/ x et en passant aux limites
x et en passant aux limites
 p c'est à
dire un taux de recombinaison
p c'est à
dire un taux de recombinaison p
où PN est la concentration de trous instantanée et
PN0 celle qu'il y aurait à l'équilibre thermique en
absence de toute perturbation on obtient alors le bilan global dans le cas d'un
modèle unidimensionnel
p
où PN est la concentration de trous instantanée et
PN0 celle qu'il y aurait à l'équilibre thermique en
absence de toute perturbation on obtient alors le bilan global dans le cas d'un
modèle unidimensionnel /
/ où
où  est la densité de charge d'espace
ce qui conduit à un système d'équations qui nous servira
pour comprendre le fonctionnement des principaux composants (et capteurs intégrés).
est la densité de charge d'espace
ce qui conduit à un système d'équations qui nous servira
pour comprendre le fonctionnement des principaux composants (et capteurs intégrés).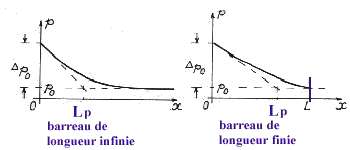
 p
tend vers zéro si
p
tend vers zéro si  1 > 0 et
1 > 0 et  2
< 0 On voit aisément que pour x = 0 on a
2
< 0 On voit aisément que pour x = 0 on a  p
=
p
=  p0 que pour
x > 0
p0 que pour
x > 0  1 et 1/
1 et 1/ 2
sont les solutions complémentaires d'une équation du second degré,
on montre aussi que lorsque le champ est élevé
2
sont les solutions complémentaires d'une équation du second degré,
on montre aussi que lorsque le champ est élevé  1
< Lp et -
1
< Lp et - 2 > Lp et il est clair que
la décroissance du nombre de trous en fonction de x est fortement dissymétrique
ainsi que le montre la représentation graphique ci-dessous (cas d'un
barreau infini des 2 côtés).
2 > Lp et il est clair que
la décroissance du nombre de trous en fonction de x est fortement dissymétrique
ainsi que le montre la représentation graphique ci-dessous (cas d'un
barreau infini des 2 côtés).contact métal-métal
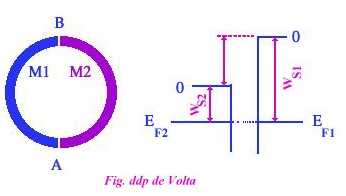
 BN
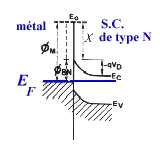
sur le plan du contact. Dans tout ce domaine il y aura appauvrissement en électrons
(on parle de région désertée) et on peut dire que la concentration
en électrons est donc une fonction croissante de x avec un champ électrique
en résultant. Ce dispositif est exploité dans les
diodes dites Schottky.
BN
sur le plan du contact. Dans tout ce domaine il y aura appauvrissement en électrons
(on parle de région désertée) et on peut dire que la concentration
en électrons est donc une fonction croissante de x avec un champ électrique
en résultant. Ce dispositif est exploité dans les
diodes dites Schottky.
 |