Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression
18 mars 2013
|
Copyright |
6 pages à l'impression |
|
version initiale 2002 | |
| dernière
mise à jour 18 mars 2013 |
PHYSIQUE DU SOLIDE
partie 7/7 : jonctions p-n
| la
base de tout |
||||
| le
stabilisateur de tension |
||||
| pour
la logique |
||||
| pour
nombre d'applications |
||||
 |
 |
 |
une collection d'icônes pour visiter tout le site | |
Deux mécanismes sont en jeu: dans le premier cas on a une jonction abrupte, c'est à dire un saut de potentiel de l'ordre de 0.3V sur quelque 0.01µm d'épaisseur ce qui correspond dans cette zone désertée à un champ de quelques 10000 V/cm augmentant avec la polarisation inverse croissante jusqu'à ce qu'il soit suffisant pour faire passer la quasi totalité des électrons de la bande de valence dans la bande de conduction, il y a alors claquage (auto-accéléré par l'effet Joule résultant de cette augmentation considérable du courant).
Fig. Jonction P-N
A l'état d'équilibre les courants d'électrons se compensent (jn = 0), il en est de même pour les courants de trous. De l'expression de ces courants vue précédemment on tire facilement pour les trous(avec E négatif). Par ailleurs, Einstein a établi une relation liant D et µ avec la température
dont on déduit immédiatement dp/p qui s'intégrera facilement Logp = -qV/kt + constante. La constante d'intégration est obtenue grâce aux conditions aux limites : pour x = - infini on a une concentration en trous maximale pp0 (valeur liée au dopage) et pour x = + infini on est dans la zone N et la concentration en trous minoritaires sera pn0 d'où le résultat
en remplaçant pp0 = Na et pn0 = (ni)2/Nd puisque tous les atomes de dopant sont ionisés à la température T . Dans la zone désertée au voisinage de l'interface on a donc
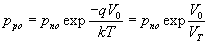
Si l'on insère cette jonction dans un circuit fermé alimenté par un champ électromoteur de telle sorte qu'à la ddp Vo s'ajoute une ddp V aux bornes de la jonction, la relation entre les deux grandeurs pn0 et pp0 est modifiée du fait que la ddp au droit du plan x = 0 est maintenant Vo-V. La relation est semblable en remplaçant simplement Vo par Vo-V et pn0 par une quantité que l'on va appeler pn(0) et dont on ne connait plus la valeur puisque le champ créé par l'adjonction de V va modifier les processus de diffusion des porteurs.
En égalant les deux expressions on obtient[1]
Si l'on s'intéresse maintenant au courant de trous traversant l'interface de gauche à droite il résulte, à une abscisse x donnée, de la somme de 2 termes, d'une part, la concentration d'équilibre pn0 et, d'autre part, une concentration due au courant de diffusion qui varie selon une loi exponentielle décroissante soit[2]. En exprimant à partir de ces diverses données [1] et [2] l'expression du courant de trous
devient alors
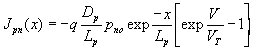
et un raisonnement semblable conduit dans la zone p à l'expression d'un courant d'électrons
En régime permanent en tout point la somme des courants Jpn(x) et Jnp(x) est constante. On peut la déterminer dans le cas limite x = 0
si V > 0 on voit que le courant est nul pour V = 0 et croît exponentiellement avec V. Si V < 0 le courant change de signe, il varie rapidement avec les faibles valeurs de V mais l'exponentielle tend très vite vers zéro et alors le courant devient constant, c'est le courant dit de polarisation inverse.
Effet Zener
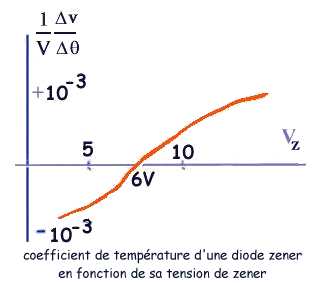
La caractéristique courant-tension d'une jonction p-n telle qu'elle résulte des équations ci-dessus comporte deux parties : une caractéristique dite directe de type exponentielle à partir d'un seuil (0.6V environ) et une caractéristique inverse caractérisée par un courant inverse très faible Js (quasi confondu avec l'axe compte tenu du choix d'unité sur le graphique ci-dessous) jusqu'à une valeur Vz de la tension inverse pour laquelle un nouveau processus se produit avec accroissement intense du courant inverse.
caractéristique d'une jonction p-n optimisée en diode zener
en polarisation
inverse cette résistance est énorme. Par contre en polarisation
directe, V étant faible aux bords de la jonction, on voit qu'en première
approximation Rd = kT/qi. Tant que i est faible cette relation suffit;
cependant lorsque i est important on ne peut négliger la chute de tension
dans le volume hors zone désertée du semiconducteur de résistance
rd dont la résistance directe totale devient alors Rd
+ rd.
/
)qNa ce
qui après deux intégrations successives donne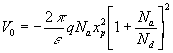 
En prenant pour origine des potentiels x = 0 on obtient V = Vp en xp,
ce qui donne la valeur de la constante. Le même raisonnement pour la partie
gauche conduit à un terme semblable 
les deux expressions de V sont évidemment égales en x = 0 d'où
l'on tire
et Na xp = - Nd xn en différentiant
l'expression de Vo par rapport à xp on peut obtenir en divisant
dQa/dV = Ci capacité dynamique de la jonction polarisée
en inverse
on voit
que cette capacité varie comme l'inverse de l'épaisseur de la
zone désertée.Il résulte de l'ensemble des propriétés mathématiquement démontrées ci-dessus un certain nombre de conséquences pratiques contraignantes et parfois contradictoires quant aux possibilités d'utilisation du Silicium et des autres semiconducteurs dans des composants électroniques, d'une part, et des microcapteurs intégrés, d'autre part.Conclusion : conséquences pratiques
B. Boittiaux, Les composants semiconducteurs, TecDoc (1995). et son site web à l'eudil
|
|
 |
|
 |
|
