Copyright
© 2000-2015
LHERBAUDIERE
7 pages à l'impression

16 mars 2013
 |
Copyright |
7 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 16 mars 2013 |
CELLULES SOLAIRES PHOTOVOLTAÏQUES
partie 1/3
|
rappels et constats désabusés |
||||
| la
pénétration d'un photon |
||||
| celui
qui nous intéresse ici |
||||
| une collection d'icônes pour visiter tout le site | ||||
L'exploitation de l'énergie solaire gratuite et quasi-illimitée suscite évidemment de grands espoirs, la cellule photovoltaïque a priori est l'un des moyens privilégiés de cette exploitation. Il en existe d'autres, mais nous n'aborderons ici que les procédés faisant appel à la photoélectricité dans les jonctions p-n. Exploiter la cellule photovoltaïque est cependant beaucoup plus facile à dire qu'à faire. Les problèmes sont effectivement nombreux :Enjeu économique
"Despite their low power density, renewable sources of energy do seem to present rather fewer environmental problems than the use of fossil fuels or nuclear power.
Solar energy is one such source and is of course indispensable to human life in many ways. Suggestions have been made to extend the use of this energy source to replace fossils fuels and nuclear power for some tasks. Solar energy is permanently available on any human time scale".Ces quelques lignes extraites du rapport britannique "Energy and the Environment " rédigé par Lord Nathan [1] pour la Royal Society of Arts en 1974, constituent une excellente introduction au problème que nous allons tenter de cerner maintenant.
| paroi orientée sud | verticale | inclinée à 60° | horizontale |
| janvier | 1.75 | 1.8 | 0.5 |
| février | 2.3 | 2.35 | 0.83 |
| mars | 3.3 | 3.9 | 1.4 |
| avril | 2.9 | 4.0 | 1.9 |
| mai | 2.5 | 4.1 | 2.4 |
| juin | 2.4 | 3.9 | 2.5 |
| juillet | 2.45 | 3.85 | 2.45 |
| aout | 2.6 | 3.85 | 2.04 |
| septembre | 3.0 | 3.8 | 1.45 |
| octobre | 2.9 | 3.0 | 1.1 |
| novembre | 1.9 | 1.9 | 0.65 |
| décembre | 1.5 | 1.6 | 0.45 |
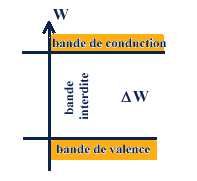
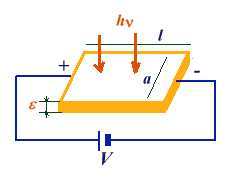
Avant d'aborder l'effet photovoltaïque nous allons rappeler quelques mécanismes élémentaires [2]. On dit qu'il y a photoconductivité chaque fois que la résistance électrique d'un corps matériel varie lorsqu'on l'éclaire avec des radiatons électromagnétiques appartenant aux domaines visible, ultra-violet et/ou infrarouge. Pour que ce phénomène puisse se produire et qu'on puisse l'observer deux conditions nécessaires mais non suffisantes doivent être remplies :Mécanisme de la photoconductivité
 0
au dessus de laquelle la photoconductivité ne peut se manifester.
0
au dessus de laquelle la photoconductivité ne peut se manifester.| -
Avant d'aller plus loin et d'établir quelques équations
assez représentatives du phénomène, il convient
de réfléchir aux conséquences pratiques de ce qui
a été énoncé ci-dessus (ce qui n'est malheureusement
pas fait la plupart du temps ni par les utilisateurs, ni par les concepteurs,
ni bien évidemment par les gouvernants dont l'ignarité
est patente - et même croissante en ce début de 21ème
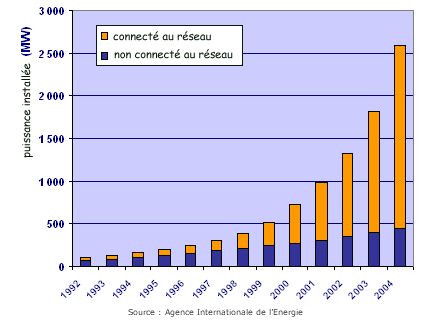
siècle). Nous venons de constater en effet que l'énergie
solaire n'est pas uniforme dans le temps,
d'une part, et qu'elle est, en outre, constituée d'un ensemble
de rayonnements IR, visible, UV et au delà, dont les effets vont
être rarement additifs, mais au contraire contradictoires.
- En effet, l'exploitation de l'énergie solaire pour la production d'électricité implique l'absorption de photons dans un matériau de type semi-conducteur pour créer ce qu'on a appelé des paires électron-trou. Malheureusement les IR n'ont pas une énergie suffisante pour provoquer le processus permettant à un électron de quitter son atome originel pour participer à la conduction. Qu'est-ce que cela signifie? Tout simplement que les IR heurtant une surface semiconductrice ne vont avoir pour conséquence que d'augmenter sa température. Et cette augmentation de la température se traduit, ainsi qu'on l'a vu dans le chapitre traitant de la résistivité par une augmentation de l'agitation des noyaux, c'est à dire une gène accrue au déplacement des électrons. Donc une partie de l'énergie solaire va avoir un effet négatif dans la conversion d'énergie radiative en énergie électrique. - Considérons maintenant, à l'autre extrémité du spectre solaire, le rayonnement UV lointain et le rayonnement X. Ces photons ont eux une très grande énergie, bien supérieure au seuil pour créer des paires électron-trou. Il en résulte qu'une partie de l'énergie de ces photons va effectivement servir à cette création et que l'excédent va seulement servir à augmenter la vitesse de notre électron. Et il en est des électrons comme des automobiles, si leur énergie (leur vitesse) est trop élevée il va y avoir de nombreuses collisions. Or à chaque fois qu'un électron semi-libre entre en collision avec une autre particule quelle qu'elle soit, la plus grande partie de son énergie est perdue, c'est à dire se transforme en chaleur. Chaleur qui contribue à augmenter la température du matériau et donc l'agitation des noyaux et, in fine, contribue à aggraver la gêne au déplacement des électrons. - Donc il est clair que l'optimisation du rendement des systèmes solaires de production d'électricité va imposer que ceux-ci soient maintenus à basse température via un système de refroidissement lui-même consommateur d'énergie ou qu'un filtre adapté empêche simultanément l'arrivée des infrarouges et des UV lointains sur le dispositif. Malheureusement on ne dispose d'aucune possibilité efficace d'empêcher certains rayonnements solaires d'arriver et, il ne faut pas rêver, c'est IMPOSSIBLE. En conséquence, quel que soit le procédé qu'on va imaginer, il ne pourra donner de résultats pharamineux et les rendements de conversion resteront dérisoires. |
 |
h
|

 ,
on exprime alors le gain de photoconduction par :
,
on exprime alors le gain de photoconduction par : rôle des piègesLes résultats expérimentaux montrent que la relation entre I et P ne suit pas tout à fait la loi que l'on vient d'écrire. En particulier lorsque le nombre de photons absorbés est faible, la relation est alors linéaire et ce n'est que lorsque la densité de photons dépasse une certaine limite que l'on se rapproche de
| nature | seuil (nm) | sensibilité(cm2/V.s) | durée de vie (µS) | |
| CdS | 510 | électrons:200 | trous | 106 |
| Se | 600 | 10 | ||
| CsSe | 720 | 200 | 104 | |
| GaAs | 920 | 3500 | 1 | |
| Si | 1100 | 1200 | 500 | 103 |
| Ge | 1800 | 3900 | 1900 | 103 |
| PbSe | 4000 | 1200 | 475 | 10 |
| PbTe | 5000 | 1175 | 870 | 1 |
| Si dopé In | 9000 | 66K | ||
| Si dopé B | 30000 | utilisables en dessous de | 20K | |
| Ge dopé Au | 15000 | 38K | ||
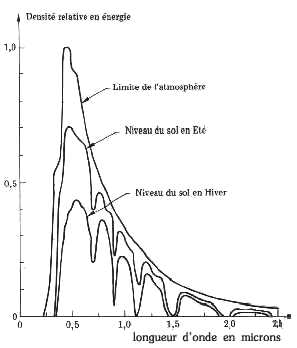
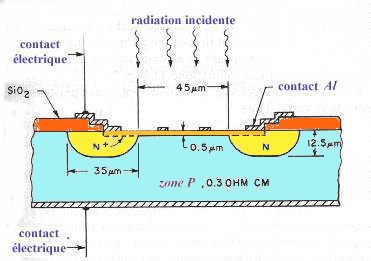
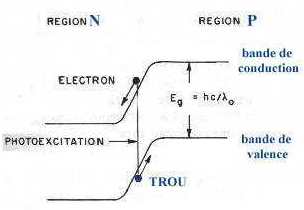
Considérons une jonction p-n et refermons ses électrodes par un court-circuit. On sait que, dans ces conditions, de part et d'autre de la jonction, sur une épaisseur petite, mais finie, règne une zone désertée dans laquelle existe un champ électrique intense produit par une ddp de quelques dixièmes de volt. Le circuit extérieur n'est le siège d'aucun courant.Effet photovoltaïque
 .
.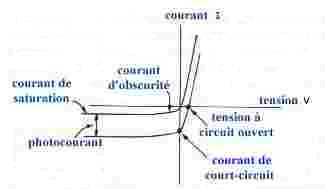
i = hq Nl G
 I/
I/ V
pour V=0 où R représente la résistance dynamique et vaut
kT/qIs ce qui, introduit dans l'expression du photocourant, nous
permet d'exprimer la tension en circuit ouvert V0.
V
pour V=0 où R représente la résistance dynamique et vaut
kT/qIs ce qui, introduit dans l'expression du photocourant, nous
permet d'exprimer la tension en circuit ouvert V0.
On peut utiliser ces cellules de deux façons distinctes : soit en série avec une fem comme détecteur de rayonnement IR (photodiodes au Ge), soit comme générateur en les refermant sur une charge R.V0 = hPllkT / hcIs, où Pl représente la puissance monochromatique reçue.