
Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression

17 mars 2013
 |
Copyright |
6 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 17 mars 2013 |
PHYSIQUE DU SOLIDE
partie 2/7 : solide et cristal
| l'association
d'atomes isolés |
||||
| ses
caractéristiques |
||||
| une collection d'icônes pour visiter tout le site | ||||
Dans le cas d'un solide les règles fondamentales de la mécanique quantique et le principe de Pauli restent valables. Cependant dans le solide les atomes ne sont plus isolés, mais au contraire rapprochés, et les électrons, tout particulièrement les plus périphériques, seront soumis à des interactions supplémentaires provenant des champs résultant de la proximité des autres noyaux et de leur cortège électronique.Solide
Tant qu'ils sont suffisamment éloignés, le champ électrique local en un point à l'intérieur du volume occupé par A n'est pas influencé par la présence de B. Par contre, dès que la distance entre les deux noyaux devient de l'ordre de 6 fois le rayon atomique les charges de B influencent celles de A et réciproquement, ce qui revient à dire que les trajectoires des électrons, en particulier les plus externes, sont perturbées.A cet effet, examinons ce qui se passe lorsqu'on rapproche deux atomes A et B préalablement supposés isolés, c'est à dire supposés seuls et non soumis à une quelconque influence extérieure.
Lorsqu'on va associer non plus deux atomes mais N, ce processus va se reproduire dans toutes les directions, on aura alors constitué un morceau de matière solide. Si les atomes sont tous de même nature, on pourra obtenir un "cristal" homogène avec une répartition régulière des atomes (en 3 dimensions) à laquelle on pourra faire correspondre une variation tout aussi régulière du champ électrique (en moyenne statistique). On notera alors qu'à chaque fois qu'un électron se trouvera dans la zone volumique commune à 2 atomes il sera impossible de le considérer comme appartenant à l'un plutôt qu'à l'autre.
Bien évidemment l'électron qui semblait appartenir à l'atome A, lorsqu'il va se trouver dans la zone intermédiaire à A et B, va voir, comme à tout instant, sa trajectoire affectée par les divers champs instantanés dus à l'ensemble des noyaux voisins et leurs électrons dont les positions instantanées sont absolument imprévisibles et il peut arriver que la résultante de ces champs soit telle que l'électron considéré va voir sa trajectoire modifiée au point qu'il va passer dans l'espace spécifique de l'atome B et devenir alors un électron de l'atome B. Plus encore, il peut lui arriver ensuite le même avatar lorsqu'il passera dans l'espace commun à B et un troisième atome C et il va passer sous le contrôle de C et on a alors typiquement le phénomène extrêmement important, pour ses conséquences industrielles, qu'on appellera la conduction. Ce processus, sur lequel on reviendra longuement, affectera évidemment beaucoup plus facilement les électrons les plus excentrés par rapport au noyau.
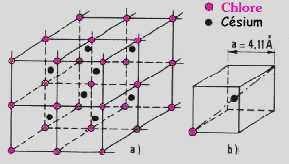
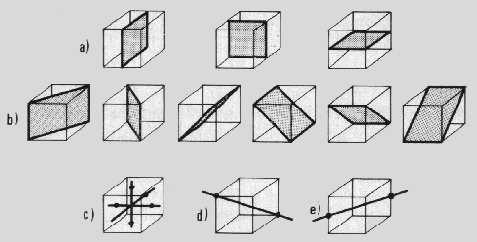
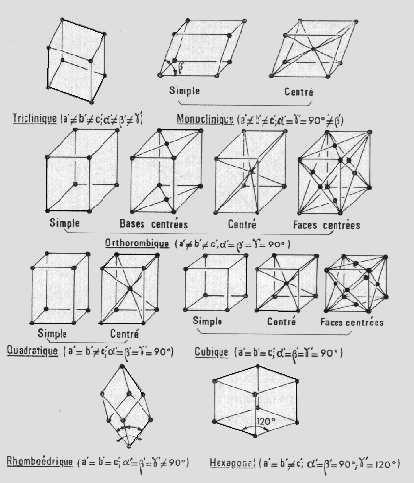
Les cristaux naturels ont toujours fasciné les hommes mais ce n'est que relativement récemment qu'on a étudié leur structure atomique, après la découverte, vers 1912, de la diffraction des rayons X par les cristaux. A l'échelle microscopique un cristal est caractérisé par un empilement régulier des ions, mais en changeant l'orientation d'examen d'un cristal on constate généralement que cet empilement varie, c'est à dire qu'on aura souvent une certaine anisotropie des propriétés macroscopiques d'un cristal. La manifestation la plus apparente de cette anisotropie est l'existence de faces naturelles et de plans de clivage à la différence de ce qui se produit dans un matériau amorphe tel le verre ou l'empilement des noyaux est chaotique et se traduit statistiquement par des propriétés physiques parfaitement isotropes.cristal
 ......
......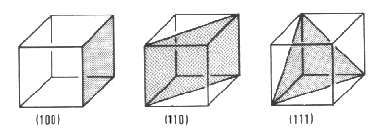
 faisant un angle
faisant un angle  avec les plans on montre
que les rayons réfléchis seront en phase et donc la réflexion
d'intensité maximale si
avec les plans on montre
que les rayons réfléchis seront en phase et donc la réflexion
d'intensité maximale si 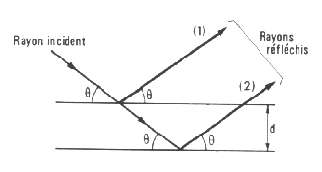
| |
|
|
 |