
Copyright
© 2000-2015
LHERBAUDIERE
2 pages à l'impression

17 mai 2013
 |
Copyright |
2 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 17 mai 2013 |
PHYSIQUE DU SOLIDE
partie 1/7 : l'atome isolé
| préambule sur la physique nucléaire | physique ou métaphysique? | |||
| atome isolé | une représentation à l'échelle | |||
| conséquences pratiques | l'association d'atomes isolés | |||
| retour à la mécanique quantique | comment les remplir | |||
| une collection d'icônes pour visiter tout le site | ||||
| Rappels fondamentaux : l'objectif de ce chapitre est de rappeler l'importance de certains paramètres dans le comportement des matériaux conducteurs et semiconducteurs et d'en déduire quelques conséquences quant à la technologie des composants et des capteurs. |
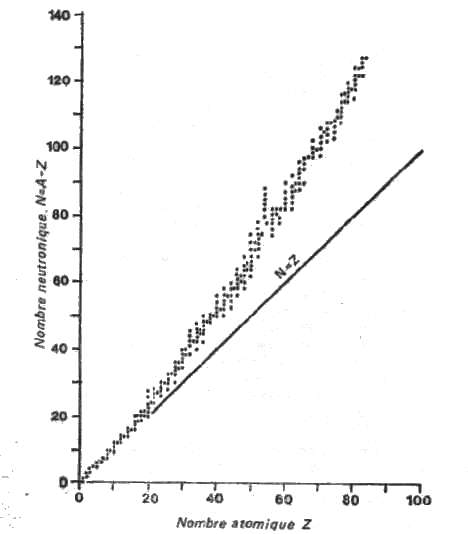
| Un atome isolé, de masse atomique A, de numéro atomique Z, peut être considéré, en première approximation, comme un noyau de charge électrique +Ze autour duquel gravitent Z électrons de charge -e. Cette approximation est extrêmement simpliste et ne permet pas de comprendre la réalité de la structure de la matière. Nous allons donc introduire quelques notions complémentaires indispensables sans pour autant faire un cours de mécanique quantique ni de physique nucléaire. |
| |
les
conséquences pratiques :
1. En fait si l'espace occupé par un atome
correspond à un volume instantané sensiblement constant, ce
volume n'est pas figé dans l'espace. En effet on constate que les noyaux
oscillent (attention cette oscillation se produit dans les 3 dimensions)
autour d'une position moyenne fixe et que l'amplitude moyenne de cette oscillation
est fonction de kT. L'espace occupé par les électrons en orbite
autour du noyau va donc subir lui aussi une déformation consécutive
à cette oscillation du noyau et, elle aussi, liée à la
température. La conséquence dans un solide est que lorsque la
température s'accroît le volume occupé par ce solide va
augmenter également, c'est ce qu'on appelle la dilatation.
2. La seconde conséquence de
l'oscillation des noyaux c'est évidemment une perturbation du champ
électrique auquel est soumis un électron libre, comme ces oscillations
ne sont ni synchrones ni de direction semblable pour tous les atomes on imagine
aisément que la conséquence en sera une gêne accrue du
déplacement de ces électrons ce qui se traduit dans notre modèle
actuel de l'atome par le coefficient de température de la résistivité.
Ce coefficient diffère d'un matériau à l'autre évidemment
puisque les noyaux ont des nombres de protons différents d'un matériau
à l'autre (ce qui a donc une incidence différente sur les fluctuations
locales de champ électrique). Notons que les neutrons, en raison de
leur neutralité, n'ont pas d'influence directe sur le champ électrique.
Cependant en raison des forces de cohésion du noyau qui interviennent
entre eux et les protons, d'une part, et de leur mobilité, d'autre
part, ils ont donc une influence extrêmement complexe et impossible
à mettre en équation sur le déplacement des protons et
donc une influence indirecte sur le champ électrique et donc
sur le déplacement des électrons. La conséquence fondamentale
en est qu'il est absolument impossible de déterminer la trajectoire
d'un électron ni mathématiquement ni même en exploitant
un procédé physique quelconque, on ne pourra jamais qu'évaluer
(avec une certaine incertitude) un processus moyen de déplacement d'un
ensemble d'électrons.
3. En pratique tous les phénomènes
physiques mettant en jeu des électrons libres ou liés vont donc
être plus ou moins sensibles à la température ce qui pourra
souvent être une difficulté, mais, a contrario, fournira
de très nombreuses possibilités de déterminer la valeur
de la température d'un matériau solide (et donc de multiples
capteurs potentiels).
4. Le fait que l'espace occupé
par les électrons soit très peu rempli va nous permettre de
comprendre pourquoi il est possible de déformer un solide en
lui appliquant des forces judicieusement choisies et pourquoi il est possible
de substituer dans un monocristal parfaitement organisé quelques
atomes par d'autres sensiblement différents et pourquoi dans un polycristal
des cristaux d'orientations différentes peuvent cohabiter. Si les atomes
étaient des sphères pleines, de dimension extérieure
différente d'un atome à l'autre, aussi faible soit cette différence,
les substitutions seraient impossibles de même que des orientations
cristallines différentes dans un même solide.
5. Une autre conséquence de
cette importance du vide est que diverses particules pourront pénétrer
à l'intérieur du solide et interagir avec des électrons
de celui-ci situés dans des atomes relativement éloignés
des surfaces limites du solide, et même parfois traverser intégralement
celui-ci (si la distance à franchir est raisonnable).
6. Enfin le lecteur comprendra qu'un
solide est finalement quelque chose ayant une certaine permanence de
l'ensemble de ses propriétés d'une extrémité à
l'autre, mais que si l'on y regarde de plus près, à un instant
t, on peut avoir (et on a généralement) des différences
notables d'un point à un autre, différences qui vont
évoluer en permanence dans le temps de telle sorte qu'on pourra avoir
des valeurs macroscopiques (pour un ensemble significatif d'atomes
voisins) moyennes constantes et identiques. Ceci est d'une extrême
importance : les propriétés macroscopiques sont donc mesurables
et peuvent figurer dans des tables de référence. Par contre
si l'on s'intéresse à des éléments solides de
très faible dimension, c'est à dire contenant un nombre d'atomes
très faible (de l'ordre du millier ou en dessous) on s'aperçoit
que l'existence et la répartition des défauts de structure vont
jouer un rôle capital et que les propriétés de deux éléments
de même taille ne pourront alors plus être systématiquement
considérées comme macroscopiquement semblables. En d'autres
termes, la miniaturisation de plus en plus poussée à laquelle
on assiste dans la réalisation des composants électroniques
a une limite en dessous de laquelle la similitude
de comportements d'éléments voisins dans un circuit ne peut
plus être garantie. Nous reviendrons sur ce point dans les chapitres
consacrés à la technologie des composants.
Relativisons :
Enfin n'oublions pas que la matière peut être solide, mais aussi
liquide ou à l'état gazeux. Et tout ce qui a été
précisé ci-dessus reste vrai pour ces 3 états avec parfois
des caractéristiques étonnantes dans certains "mélanges".
L'un de ces mélanges particulier est l'air dans lequel nous évoluons
et dont maints capteurs cherchent à mesurer les "propriétés",
et nous allons l'examiner sous un certain angle afin de bien faire comprendre
au lecteur la vanité de certaines mesures (vanité ou parfois
même ineptie). Je vais développer cet exemple car, au cours de
ma carrière universitaire, j'ai maintes fois eu à suivre des
stagiaires en milieu industriel et fréquemment j'ai pu constater dans
ces entreprises que l'on exploitait de manière plus ou moins erronée
des capteurs pour contrôler une fabrication ou un environnement. Et,
à chaque fois, l'erreur résultait d'une méconnaissance
de la nature réelle du milieu concerné, c'est-à dire
d'une confusion entre les modèles simplistes utilisés dans les
lycées pour présenter la structure de la matière à
des élèves (peu concernés a priori par la réalité
fondamentale), et cette réelle complexité de notre environnement.
Considérons l'air
que nous respirons. C'est un mélange de gaz : azote oxygène
qui sont des molécules diatomiques, des gaz rares monoatomiques, et
divers ingrédients que l'on pourrait ranger sous le vocable
"polluants" dont la liste est longue et dont les concentrations
sont infiniment variables d'un lieu à un autre et d'un moment à
l'autre. Dans ces ingrédients on trouve la vapeur d'eau qui
va nous intéresser fortement puisque nous consacrons un gros chapitre
à la métrologie de l'humidité de l'air dans le module
capteurs. On montre aisément que la quantité maximale possible
d'eau à l'état de vapeur varie avec la température de
l'air, et on a imaginé divers capteurs pour identifier la situation
de l'air humide en un lieu et un instant donné, c'est à dire
pour exprimer le pourcentage du maximum possible de vapeur d'eau présent
dans l'air analysé, ce qu'on appelle couramment l'humidité relative.
L'expérience montre que nombre de capteurs arrivent à suivre
la variation de l'humidité relative lorsqu'elle est très faible
(c'est à dire lorsque l'air est plutôt sec) mais que lorsque
on approche du maximum (de la saturation) souvent les temps de réponse
des capteurs augmentent considérablement et les mesures dynamiques
n'ont alors plus aucun sens.
Que ce passe-t-il? Un gaz ce sont des atomes et/ou des molécules qui
sont très éloigné(e)s les un(e)s des autres ce qui leur
permet de se déplacer énormément, de se heurter élastiquement,
et tout ce que nous avons dit ci-dessus des propriétés "moyennes"
est encore plus vrai. A 20°C la quantité de vapeur d'eau maximale
possible dans l'air est sensiblement de 20g d'eau par kilogramme d'air. Dans
de l'air très sec on aura par exemple moins de 1g/kg, soit très
grossièrement une molécule d'eau isolée dans un millier
de molécules d'oxygène, azote, etc (qu'on va appeller par commodité
des molécules d'air)...Ces molécules d'air sont électriquement
neutres et "en moyenne" symétriques et n'ont donc pas une
très grosse influence sur le comportement des molécules d'eau
isolées.
Par contre les molécules d'eau H2O sont polaires car les axes moyens
(avec toutes les restrictions concernant ces moyennes statistiques)
entre les atomes d'hydrogène et celui d'oxygène forment un angle
de 120° et le noyau de l'oxygène comportant plus de protons que
celui de l'hydrogène, il en résulte que les trajectoires des
électrons des 2 atomes d'hydrogènes sont déformées
et statistiquement plus proches de O. Quand le taux d'humidité relative
de l'air approche du maximum cela correspond grossièrement dans notre
exemple à 2 molécules d'eau en moyenne dans une centaine
de molécules d'air. Il est donc plausible qu'en certains points du
mélange, eu égard au déplacement permanent des molécules
de gaz, plusieurs molécules d'eau se rencontrent et restent 'en contact"
en raison de leur polarité et de leur géométrie particulière...et
elles forment alors des nanogouttelettes d'eau. Ces nanogouttelettes n'ont
plus les propriétés physiques d'un gaz, mais celles de l'eau
liquide et dans ce cas l'emploi d'un capteur basé sur la mesure d'une
propriété physique des gaz devient inapproprié. Le problème
est alors le suivant : à partir de quel moment la mesure n'a plus de
sens? La réponse est impossible à donner puisqu'on ignore si
les molécules d'eau au voisinage du capteur se sont ou non agglomérées.
On peut juste dire que c'est une éventualité.
J'espère qu'au
vu de cet exemple, pris parmi bien d'autres possibles, le lecteur comprendra
que la notion de propriétés statistiques moyennes peut elle
même être prise en défaut et qu'on doit faire preuve de
beaucoup d'humilité devant la complexité de notre environnement.
Pauli a montré par ailleurs que deux électrons ne pouvaient se trouver rigoureusement dans le même état énergétique au même instant (c'est à dire qu'ils devaient différer au moins par l'un de leurs quatre nombres quantiques). Il en résulte que pour un atome isolé de numéro atomique Z, et ayant donc Z électrons, seuls Z niveaux seront occupés à un instant donné et, dans l'état dit fondamental, ce seront les Z niveaux de plus basse énergie.
- n : la couche électronique à laquelle appartient l'électron, n=0, 1, 2, etc. Les chimistes ont pris l'habitude de nommer ces couches K, L, M, N, O, P...La couche K peut contenir 2 électrons, L: 8 électrons, M: 18, etc. Mais l'expérience montre que pour l'ensemble des matériaux dits "éléments de transition" la couche M n'est pas complète alors qu'il y a des électrons dans la couche N supérieure (ainsi par ex. le potassium comporte 2K, 8L, 8M, 1N). Ceci résulte du fait qu'il y a peu de différence entre les niveaux énergétiques les plus élevés de la couche M et ceux les plus bas de la couche N. Il en résultera des propriétés physiques particulières sur lesquelles nous reviendrons dans d'autres chapitres. En pratique c'est la couche la plus périphérique, donc celle de valeur n la plus élevée, qui va jouer le rôle essentiel dans les propriétés qui nous intéresseront.
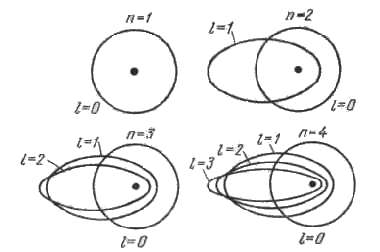
- l : l'excentricité de la trajectoire l varie de 0 à n-1
- m : la projection de son moment magnétique sur un axe de référence, m=n+1, n+2, etc.
- s : le spin de l'électron significatif de son sens de rotation sur lui-même il vaut +1/2 ou -1/2
 r
= n
r
= n où n, entier
positif, représente le numéro de la couche électronique
et
où n, entier
positif, représente le numéro de la couche électronique
et  l'onde associée à l'électron,
dont on peut montrer qu'elle vaut
l'onde associée à l'électron,
dont on peut montrer qu'elle vaut  =h/mv
où h est la constante dite de Planck.
=h/mv
où h est la constante dite de Planck.