
Copyright
© 2000-2015
LHERBAUDIERE
8 pages à l'impression

22 mars 2013
 |
Copyright |
8 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 22 mars 2013 |
première partie (1/3)
| cas du capteur idéal | idéal,on connait les équations | |||
| signaux aléatoires | le bruit dans tous ses états | |||
| l'analyse de Fourier | l'exploitation d'une technique spectrale | |||
| les méthodes par ondelettes | une autre approche parfois mieux adaptée | |||
| une collection d'icônes pour visiter tout le site | ||||
Cette situation est malheureusement exceptionnelle et le plus souvent la fonction de transfert n'est pas linéaire, des grandeurs d'influence et des bruits perturbent le résultat. Parfois même l'équation reliant la grandeur à mesurer et la sortie du capteur n'est pas de type paramétrique. A chacun de ces problèmes correspondent des approches spécifiques de traitement du signal.
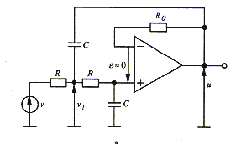
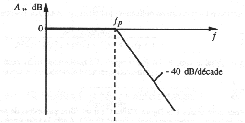
 3.1. Spectre
du bruit extérieur au spectre du signal utile
3.1. Spectre
du bruit extérieur au spectre du signal utile
 .....
.....
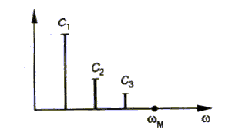
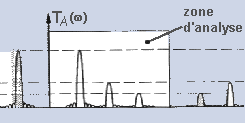
 3.2. Spectre
du bruit aléatoire et recouvrant la plage de signal utile
3.2. Spectre
du bruit aléatoire et recouvrant la plage de signal utile
 ...
...
La transformation de Fourier est un outil majeur dans l'analyse du signal. Elle est incontournable dans l'analyse du signal utilisant l'aspect fréquentiel d'un signal. En effet, une description fréquentielle est souvent plus " lisible " que la description temporelle et est un complément remarquable à la seule description temporelle. La transformation de Fourier associée à s(t) s'écrit :3.2.1 de Fourier à l'ondelette de Morlet
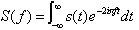
 at),
où le terme b localise une fenêtre d'analyse. Cette transformation s'écrit:
at),
où le terme b localise une fenêtre d'analyse. Cette transformation s'écrit:

 f se
définit par :
f se
définit par :  f représente la
résolution en fréquence, autrement dit deux sinusoïdes peuvent être discriminées
si elles sont différentes de plus de
f représente la
résolution en fréquence, autrement dit deux sinusoïdes peuvent être discriminées
si elles sont différentes de plus de  f.
De la même façon, la résolution en temps
f.
De la même façon, la résolution en temps  t
se définit par:
t
se définit par:  t représente la résolution
en temps, et deux impulsions peuvent être discriminées si elles sont espacées
de plus de
t représente la résolution
en temps, et deux impulsions peuvent être discriminées si elles sont espacées
de plus de Pour palier la limitation de résolution du TFFG, J. Morlet a repris la démarche de Gabor en choisissant la fonction3.2.2 transformation en ondelettes
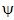 différente de g. Pour que
différente de g. Pour que  t
et
t
et  f varient dans
le plan temps-fréquence, la famille de
f varient dans
le plan temps-fréquence, la famille de 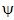 n'est pas construite par translation et modulation comme celle de g, mais par
translation et dilatation
ou contraction ( changement d'échelle). La fonction
n'est pas construite par translation et modulation comme celle de g, mais par
translation et dilatation
ou contraction ( changement d'échelle). La fonction
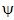 (t), de la variable réelle
t, s'appelle " ondelette mère ". Le nom d'ondelette vient du fait que c'est
une fonction oscillante (comme une onde), mais localisée. Ces conditions suggèrent
que
(t), de la variable réelle
t, s'appelle " ondelette mère ". Le nom d'ondelette vient du fait que c'est
une fonction oscillante (comme une onde), mais localisée. Ces conditions suggèrent
que 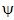 (t) vibre comme une onde
et décroît rapidement quand |t| augmente. La famille d'ondelettes
(t) vibre comme une onde
et décroît rapidement quand |t| augmente. La famille d'ondelettes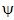 a,b(t),
a>0, b
a,b(t),
a>0, b R s'écrit :
R s'écrit : 

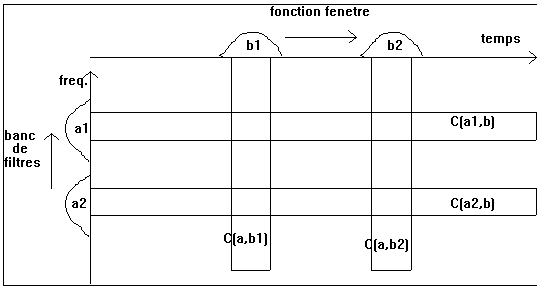
 fonctions analysantes et résolution temps fréquence
de TFFG (a) et TO (b)
fonctions analysantes et résolution temps fréquence
de TFFG (a) et TO (b)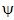 a,b
comme un banc de filtres, la résolution en temps augmente avec la fréquence
centrale des filtres. Et
a,b
comme un banc de filtres, la résolution en temps augmente avec la fréquence
centrale des filtres. Et  f
n'est plus constant mais proportionnel à la fréquence centrale :
f
n'est plus constant mais proportionnel à la fréquence centrale :  f/f=
c Le banc de filtres est composé par un ensemble de filtres passe bande avec
une largeur de bande relative constante. Une autre façon de voir est de dire
qu'au lieu que les filtres soient régulièrement espacés dans l'échelle linéaire
(comme dans TFFG), les filtres sont régulièrement répartis dans l'échelle logarithmique.
f/f=
c Le banc de filtres est composé par un ensemble de filtres passe bande avec
une largeur de bande relative constante. Une autre façon de voir est de dire
qu'au lieu que les filtres soient régulièrement espacés dans l'échelle linéaire
(comme dans TFFG), les filtres sont régulièrement répartis dans l'échelle logarithmique.
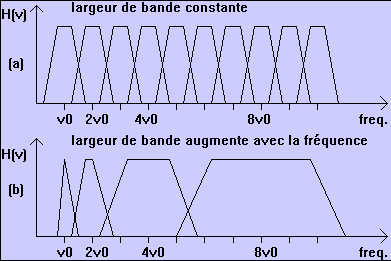
 division du domaine fréquentiel (a) pour TFFG
(couverture uniforme) et (b) pour TO (couverture logarithmique)
division du domaine fréquentiel (a) pour TFFG
(couverture uniforme) et (b) pour TO (couverture logarithmique)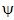 est dite ondelette
analysante si elle satisfait les conditions suivantes [BAR91] :
est dite ondelette
analysante si elle satisfait les conditions suivantes [BAR91] :
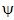 (a,b)
forment une famille d'ondelettes de même énergie. L'ensemble de fonctions Sa,b
constitue la décomposition du signal s(t) suivant la famille d'ondelettes
(a,b)
forment une famille d'ondelettes de même énergie. L'ensemble de fonctions Sa,b
constitue la décomposition du signal s(t) suivant la famille d'ondelettes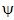 a,b.
Pour chaque couple (a,b), |Sa,b|² est proportionnel à l 'énergie du signal s(t)
contenu dans la bande de fréquence liée à
a,b.
Pour chaque couple (a,b), |Sa,b|² est proportionnel à l 'énergie du signal s(t)
contenu dans la bande de fréquence liée à 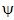 et au couple (a,b). En un certain sens Sa,b mesure les fluctuations
du signal s(t), autour du point b, à l'échelle fournie par a>0.
et au couple (a,b). En un certain sens Sa,b mesure les fluctuations
du signal s(t), autour du point b, à l'échelle fournie par a>0.
Si 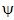 a,b
satisfait la condition d'admissibilité, alors le signal peut être restitué
par une formule de reconstruction :
a,b
satisfait la condition d'admissibilité, alors le signal peut être restitué
par une formule de reconstruction :

![]() où
où ![]()
La première famille d'ondelettes présentée par J. Morlet est issue de la fonction
: 3.2.3. ondelette de Morlet
![]()
Elle est inspirée du signal élémentaire de Gabor, c'est à dire par modulation
d'une gaussienne. Depuis, toutes les ondelettes 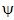 (t)
correspondant à une modulation d'amplitude d'enveloppe A(t) portée par une exponentielle
complexe, s'appellent ondelettes de type Morlet. Elle ne satisfait pas rigoureusement
à la condition d'admissibilité mais le choix de de f0 et
(t)
correspondant à une modulation d'amplitude d'enveloppe A(t) portée par une exponentielle
complexe, s'appellent ondelettes de type Morlet. Elle ne satisfait pas rigoureusement
à la condition d'admissibilité mais le choix de de f0 et ![]() permet d'approcher cette condition. La solution de compromis retenue par Morlet
consistait à imposer une valeur faible de |
permet d'approcher cette condition. La solution de compromis retenue par Morlet
consistait à imposer une valeur faible de |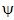 (0)|
tout en ne tolérant qu'un petit nombre d'oscillations, donc f0. La famille
d'ondelettes de Morlet donne un outil remarquable pour l'analyse de signaux.
Mais elle est redondante et ne peut en aucun cas conduire à la reconstruction
d'une base de L²(R).
(0)|
tout en ne tolérant qu'un petit nombre d'oscillations, donc f0. La famille
d'ondelettes de Morlet donne un outil remarquable pour l'analyse de signaux.
Mais elle est redondante et ne peut en aucun cas conduire à la reconstruction
d'une base de L²(R).
La première construction de base orthonormales d'ondelettes pour L²(R) découle
de travaux de Y.Meyer [MEY87].
Il découvre qu'en choisissant la fonction analysante y de manière plus précise
(à spectre borné, de classe Ca et à décroissance rapide ) et en discrétisant
les paramètres a et b (a = 2-j, b = k2-j), alors :3.2.4. analyse multirésolution et
ondelette.
![]() forment une
base de L²(R).
forment une
base de L²(R).
La décomposition sur une base d'ondelette orthonormale signifie que le signal
est décomposé de manière unique et minimale et que les coefficients Sa,b sont
indépendants. D'autres bases ont été proposées [FLA93]. L'une des plus remarquables
est découverte par Ingrid Daubechies [DAU88]. Sa découverte a été effectuée
dans le cadre de la construction des bases d'ondelettes à support compact, de
façon à ne mettre en jeu qu'un nombre fini de coefficients dans les filtres
associés. La théorie des ondelettes se développe vraiment lorsque S. Mallat
[MAL89] propose un algorithme rapide pour le calcul des coefficients d'ondelettes.
Son algorithme s'inspire d'algorithme pyramidal introduit dans les années 70
pour la décomposition en sous-bandes. Il a montré que la théorie des ondelettes
s'intègre dans la notion d'analyse multirésolution.
Celle-ci se formalise à partir de l'idée intuitive selon laquelle tout signal
peut être construit par raffinements successifs, c'est-à-dire par l'ajout de
détails à une approximation, et l'itération du processus.
Ainsi qu'on vient de le voir un procédé récent met en oeuvre
l'analyse par ondelettes que l'on peut en première approximation considérer
comme une extension de la FFT dans laquelle la fenêtre d'analyse peut
être optimisée dans sa forme et possède en outre la propriété
essentielle d'opérer sur une durée variant avec la fréquence.
Il en résulte des possibilités accrues de filtrage avec des temps
de calcul raisonnables. Une ondelette est un signal oscillant dont la moyenne
est nulle et dont l'énergie tend vers zéro à l'infini.
Les ondelettes sont regroupées en familles de courbes formant chacune
une base de l'espace vectoriel des signaux. Il s'agit donc de décomposer
un signal selon une autre base que celle des sinusoïdes. 3.2.5.exploitation pratique
Résumons l'algorithme de Mallat
L'analyse multirésolution d'une fonction f de L²(R) se traduit par l'obtention
d'une suite discrète fn de fonctions, dont chacune est une
approximation de f à une résolution bien déterminée. Par définition,
une analyse multirésolution [MAL89] est une suite croissante {Vj}
j Z de sous-espaces vectoriels fermés de
L²(R). Chaque Vj se trouve associé à une résolution 2j et l'approximation
d'un signal f(t) à cette résolution est obtenue par projection sur le sous-espace
correspondant. Autrement dit si Pj sont des projecteurs orthogonaux
sur les espaces Vj, alors pour tout f dans L²(R) :
Z de sous-espaces vectoriels fermés de
L²(R). Chaque Vj se trouve associé à une résolution 2j et l'approximation
d'un signal f(t) à cette résolution est obtenue par projection sur le sous-espace
correspondant. Autrement dit si Pj sont des projecteurs orthogonaux
sur les espaces Vj, alors pour tout f dans L²(R) :
Pj : f L²(R) ---> Pj(f)
L²(R) ---> Pj(f) Vj et Pj(f) est une approximation de f à
une résolution 2j.
Vj et Pj(f) est une approximation de f à
une résolution 2j.
Et puisque d'après la propriété Vj Vj+1,
l'approximation Pj+1(f) est " meilleure " que l'approximation
Pj(f) :
Vj+1,
l'approximation Pj+1(f) est " meilleure " que l'approximation
Pj(f) :
Une base de Vj peut alors se déduire de la base V0 par
construction de la famille des dilatées et translatées :  k,j=2j/2
k,j=2j/2 (2jt-k)
à partir de la seule fonction
(2jt-k)
à partir de la seule fonction  (t)
appelée fonction d'échelle. Il ne s'agit pas encore de l'ondelette mais d'une
fonction parfois appelée " père des ondelettes ". Les coefficients d'approximation
Ak,j, obtenus par :
(t)
appelée fonction d'échelle. Il ne s'agit pas encore de l'ondelette mais d'une
fonction parfois appelée " père des ondelettes ". Les coefficients d'approximation
Ak,j, obtenus par : ![]() sont en fait une représentation extrêmement redondante. En reprenant l'idée
de description d'un signal en termes d'approximations successives, une représentation
beaucoup plus économique consiste à s'intéresser à la différence d'information
qui existe entre deux approximations consécutives. Cette différence, Pj+1(f)
- Pj(f), est un détail additionnel nécessaire
pour passer de l'approximation d'échelle 2j ( Pj(f)) à celle, plus
fine, d'échelle 2j+1 (Pj+1(f)). Ceci revient à dire que, pour chaque
espace d'approximation Vj, les détails appartiennent à un espace
supplémentaire orthogonal de Vj dans Vj+1.
sont en fait une représentation extrêmement redondante. En reprenant l'idée
de description d'un signal en termes d'approximations successives, une représentation
beaucoup plus économique consiste à s'intéresser à la différence d'information
qui existe entre deux approximations consécutives. Cette différence, Pj+1(f)
- Pj(f), est un détail additionnel nécessaire
pour passer de l'approximation d'échelle 2j ( Pj(f)) à celle, plus
fine, d'échelle 2j+1 (Pj+1(f)). Ceci revient à dire que, pour chaque
espace d'approximation Vj, les détails appartiennent à un espace
supplémentaire orthogonal de Vj dans Vj+1.
Inversement Y. Meyer et S. Mallat montrent que l'on peut construire une base
orthonormale d'ondelettes en partant d'une analyse multirésolution. La construction
peut être introduite de la manière suivant : on considère Wj le supplémentaire
orthogonal de Vj dans Vj+1. Ceci signifie que l'on a la
relation :
Vj+1 = Vj Å Wj
On suppose que s, le signal à analyser, est déjà approximé à une
certaine échelle. Par convention, on fixera cette échelle à j=0. Le signal
s appartient donc à V0. On introduit les variables Ak,j(s)
et Dk,j(s) qui sont respectivement les projections de s sur les
espaces d'approximation (Vj) et de détails (Wj) aux
échelles plus grossières (j<0)

![]() et
et ![]()

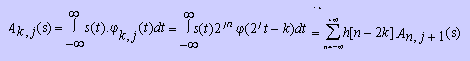 et
et ![]()
Ces deux équations ci-dessus indiquent que le calcul des coefficients d'approximation
Ak,j(s) et de détail Dk,j(s) se fait de façon hiérarchique.
A chaque étape on applique en fait dans la cellule de décomposition
deux filtres : un passe-bas, dont sera issue
une approximation Ak-1, et un passe-haut,
dont on obtiendra les détails Dk-1. En procédant
à une décimation d'ordre 2 sur
Ak-1 on pourra dans l'étage suivant utiliser les mêmes
filtres ce qui simplifie fortement l'architecture du système. Un tel
algorithme est dit pyramidal. Sa structure pyramidale est illustrée par la
figure ci-dessous.

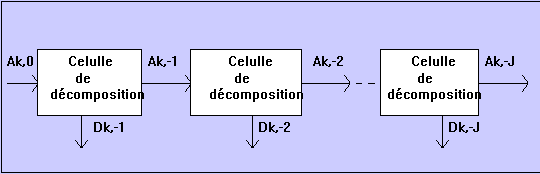
 principe de l'algorithme pyramidal de décomposition
principe de l'algorithme pyramidal de décomposition

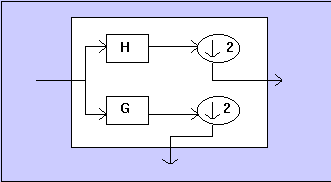
 Fig. principe de la cellule de décomposition
Fig. principe de la cellule de décomposition
Il en résulte des diagrammes plus faciles à interpréter
que ceux obtenus avec la transformée de Fourier avec une fenêtre
glissante mais sur un temps fini.
Il convient de noter que, si l'on sait, grâce à cet algorithme
pyramidal, décomposer le signal, en utilisant un processus inverse
on pourra reconstruire le signal.
La relation de reconstruction s'écrit: ![]()
Mais en omettant certains détails lors de la reconstruction, il va
de soit que l'on pourra réaliser une opération de filtrage tout
à fait élégante. L'exemple de décomposition par
l'ondelette de Mallat d'un signal électrocardiogramme fortement bruité
illustre typiquement cette possibilité.

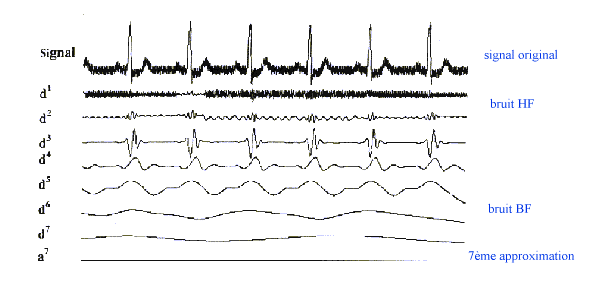
 Fig. décomposition en sept étapes d'un
signal ECG bruité
Fig. décomposition en sept étapes d'un
signal ECG bruité
![]() Sur cet exemple on constate
que le bruit HF se concentre essentiellement dans les détails d1 et
d2 que l'on supprimera de la reconstruction., tandis que le bruit basse fréquence
influence les détails d6 et d7. On constate que dans la 7ème
approximation il ne reste quasiment plus rien, il est donc inutile de continuer
la décomposition.
Sur cet exemple on constate
que le bruit HF se concentre essentiellement dans les détails d1 et
d2 que l'on supprimera de la reconstruction., tandis que le bruit basse fréquence
influence les détails d6 et d7. On constate que dans la 7ème
approximation il ne reste quasiment plus rien, il est donc inutile de continuer
la décomposition.
Enfin l'intérêt des méthodes avancées de traitement
du signal résulte de leur bonne adaptabilité au principe de
filtrage dit adaptatif dont on donne un exemple ci-après.
![]() Mais avant de continuer j'aimerai attirer votre attention sur la question
suivante : avez-vous lu la page d'accueil du site? Retournez-y et pensez un
peu plus loin que votre lecon d'électronique d'aujourd'hui. Consultez
toutes les rubriques du site. Elles ne sont pas là pour "faire
bien" mais parce qu'elles sont TOUTES complémentaires et qu'elles
vous apporteront des connaissances inédites qu'on ne trouve pas dans
les cours du lycée ou de la fac. Dites-vous bien que dans le monde
du XXIème siècle c'est votre culture (et pas seulement technique)
qui fera la différence, et n'oubliez pas notre rubrique de liens amis,
c'est votre intérêt.
Mais avant de continuer j'aimerai attirer votre attention sur la question
suivante : avez-vous lu la page d'accueil du site? Retournez-y et pensez un
peu plus loin que votre lecon d'électronique d'aujourd'hui. Consultez
toutes les rubriques du site. Elles ne sont pas là pour "faire
bien" mais parce qu'elles sont TOUTES complémentaires et qu'elles
vous apporteront des connaissances inédites qu'on ne trouve pas dans
les cours du lycée ou de la fac. Dites-vous bien que dans le monde
du XXIème siècle c'est votre culture (et pas seulement technique)
qui fera la différence, et n'oubliez pas notre rubrique de liens amis,
c'est votre intérêt.
 |
 |