
Copyright
© 2000-2015
LHERBAUDIERE
8 pages à l'impression

28 janvier 2015
 |
Copyright |
8 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 28 janvier 2015 |
deuxième partie (2/3) : filtrage et classification
| le filtrage adaptatif | un must pour éliminer le bruit | |||
| cas des capteurs non sélectifs | l'analyse multidimensionnelle | |||
| classification avec des capteurs linéaires | des graphiques complexes | |||
| avec des capteurs non linéaires | les réseaux de neurones | |||
| une collection d'icônes pour visiter tout le site | ||||
Le filtrage adaptatif
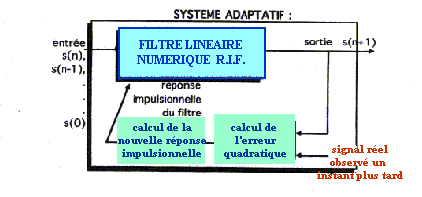

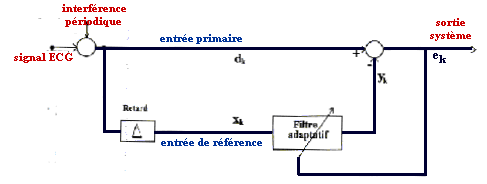

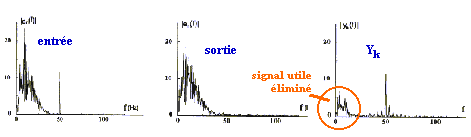

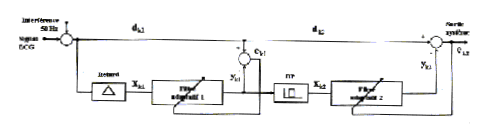

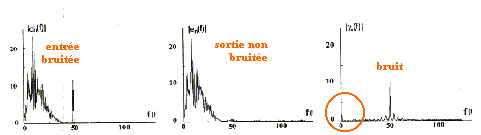
|
Un dernier cas peut se présenter : celui où l'on ne possède pas de capteur spécifique de la grandeur à mesurer, mais des capteurs répondant à plusieurs grandeurs simultanément sans que l'on puisse exprimer une réponse sous une forme mathématique paramétrique. |
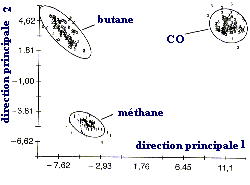
L'exemple typique de modèle pour l'acquisition de signal multidimensionnel et son traitement est l'odorat. Par le biais de divers récepteurs situés dans le nez, et se trouvant à l'extrémité d'une terminaison nerveuse, on peut traiter et identifier une grande palette d'odeurs perceptibles. Comme les capteurs chimiques non sélectifs, les récepteurs olfactifs nasaux possèdent une sensibilité influencée par la multiplicité des gaz et odeurs présents à l'instant t qui se superposent. Les signaux primaires multidimensionnels des récepteurs olfactifs (échantillons d'excitation) sont ensuite transformés dans le cerveau en échantillons de signaux de moindre dimensions (phase de mémorisation). Une reconnaissance d'odeur intervient par la comparaison de l'échantillon actuel du signal avec les modèles appris. La problématique de la sélectivité des capteurs chimiques est analogue: une série de capteurs non sélectifs, mais différents, génère un signal échantillonné qui sera caractéristique de substances individuelles et, grâce à des méthodes de reconnaissance de forme, on pourra identifier lesdites substances.Classification

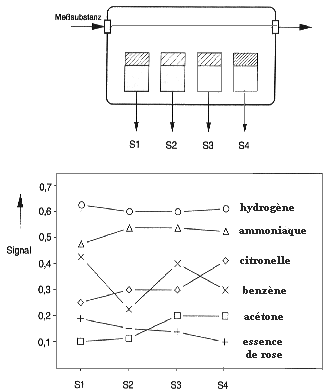
Prenons l'exemple facile de la discrimination entre deux gaz A et B avec deux éléments sensibles linéaires. Les signaux S1 et S2 peuvent être décrits en tant que fonction de la concentration gazeuse par le système d'équation (1)Classification dans le cas de capteurs linéaires

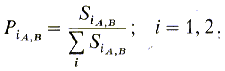 (2)
(2) 

 ..........
..........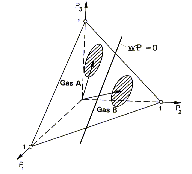
 Fig.
(a) exemple de classification, (b) limite de séparation identifiée
par une surface
Fig.
(a) exemple de classification, (b) limite de séparation identifiée
par une surface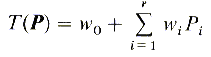 où r représente le nombre d'éléments sensibles. Si l'on ramène P à un membre
constant P0=1, la limite de séparation T entre deux classes peut
se représenter par une surface (plan) de séparation dans l'espace caractéristique
selon (4)
où r représente le nombre d'éléments sensibles. Si l'on ramène P à un membre
constant P0=1, la limite de séparation T entre deux classes peut
se représenter par une surface (plan) de séparation dans l'espace caractéristique
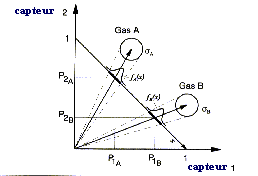
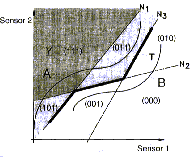
selon (4) Avec des capteurs non linéaires la procédure de normalisation pour assurer l'indépendance de la concentration n'est pas aisée. L'échantillon d'un gaz prendra donc une répartition dans l'espace caractéristique dépendant de la concentration et s'écartant donc de la répartition normée. Pour pouvoir séparer les classes de l'échantillon il faut alors introduire des fonctions de séparations non linéaires (ou linéaires par parties). La figure ci-dessous montre un exemple d'une telle répartition non linéaire de deux classes obtenues à l'aide de deux capteurs [7]. Les limites des domaines sont décrites par les courbes A et B.Problème de la classification avec des capteurs non linéaires.


 ......
......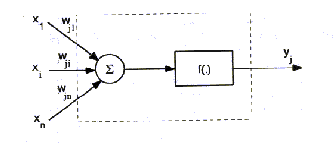
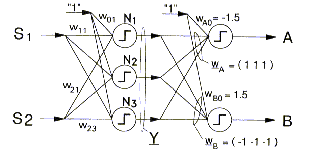
 Fig perceptron
multicouche (à gauche) et neurone artificiel élémentaire
(à droite)
Fig perceptron
multicouche (à gauche) et neurone artificiel élémentaire
(à droite)
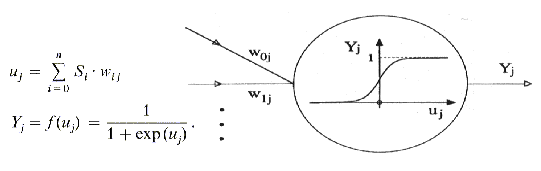
 Fig. fonction
sigmoïde et mode d'utilisation
Fig. fonction
sigmoïde et mode d'utilisation

 tableau de
résultats pour le perceptron ci-avant
tableau de
résultats pour le perceptron ci-avantSi vous souhaitez des compléments sur les réseaux de neurones allez sur le site http://asi.insa-rouen.fr/education/courses-for-foreign-students vous y trouverez un cours complet sur les réseaux de neurones, bayesiens et les applications et toutes les méthodes récentes de filtrage.
petite annonce : Ce site n'est pas une annexe d'un quelconque journal gratuit, mais il faut bien parfois déroger à la règle. Vous êtes un utilisateur de signaux divers et complexes, vous aimeriez leur faire subir un traitement adapté pour en tirer une information pertinente, mais vous ne savez pas comment faire et la lecture de ce site vous a donné des idées mais vous ne vous sentez pas suffisamment expert pour vous lancer, alors contactez mon complice Denis De Brucq, professeur émérite de l'université de Rouen et mathématicien traiteur de signal renommé, il se fera un plaisir de vous aider. Son mail : Denis De Brucq.
 |