
Copyright
© 2000-2015
LHERBAUDIERE
10 pages à l'impression

28 janvier 2015
 |
Copyright |
10 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 28 janvier 2015 |
| le synoptique général | pourquoi et comment un FPGA | |||
| réalisation d'un neurone | les différents opérateurs | |||
| réalisation d'une couche | des RAMs et des ROMs | |||
| réalisation du réseau | la reconfiguration dynamique | |||
| une collection d'icônes pour visiter tout le site | ||||
Généralités
Nous allons examiner le problème de l'analyse de la pollution atmosphérique, pour lequel nous avons par ailleurs longuement explicité les microcapteurs utilisables. L'implémentation d'un réseau de neurones a été imaginée sous forme matérielle par le biais d'un circuit FPGA dans l'objectif de réaliser un système nomade. |

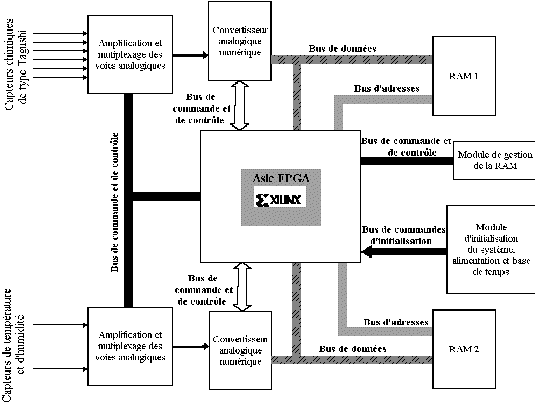
 Fig. système ambulatoire de suivi de la pollution
atmosphérique
Fig. système ambulatoire de suivi de la pollution
atmosphérique
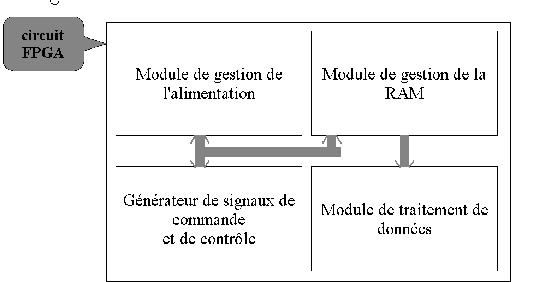
Pour l'unité de traitement, nous avons choisi la représentation des nombres réels en virgule fixe. La position de la virgule est définie arbitrairement selon l'ordre de grandeur des valeurs manipulées. Nous avons opté pour ce choix puisque les mesures issues des capteurs possèdent le même ordre de grandeur et peuvent en plus être normalisées afin de les ramener dans un intervalle donné. La normalisation de ces données peut en plus favoriser la convergence lors de l'apprentissage. Par conséquent la représentation en virgule fixe est donc bien adaptée pour répondre aux exigences du traitement, en outre les opérations arithmétiques en virgule fixe sont réalisées par des opérateurs entiers moins gourmands en silicium que les opérateurs à virgule flottante.La représentation des nombres
Il faut remettre en cause l'organisation des calculs, redéfinir les précisions de calcul et de codage des coefficients Wi trouvés lors de la phase d'apprentissage en utilisant des critères liés à la qualité souhaitée du résultat. Cette optimisation conduit à une réduction de la complexité tant au niveau algorithmique qu'architectural, en effet il faut toujours se préoccuper des performances en vitesse et de la réduction de la surface occupée lors d'une réalisation matérielle. Le problème de l'adéquation algorithme/architecture est reporté au niveau de la programmation des circuits dans un langage de haut niveau tel que le VHDL.Adéquation algorithme/architecture
La conception des opérateurs arithmétiques synthétisés sur FPGA, s'est concrétisée par l'utilisation du langage VHDL [ARM93]. L'écriture de ces opérateurs en VHDL, nous permet en phase de mise au point de nous abstraire du circuit final et nous donne toute la souplesse pour modifier ou améliorer ces circuits afin d'assurer leur évolution ultérieure. La programmation en VHDL permet aussi à partir des spécifications de " haut niveau " de rester indépendant de la technologie de placement et de la librairie de cellules logiques spécifique d'une famille de FPGA. Ceci constitue un réel avantage car l'évolution de la technologie est très rapide.Utilisation du langage VHDL
L'étude des algorithmes nous fournit le type et la taille des données manipulées afin de définir les caractéristiques de notre architecture finale. Les données peuvent êtres codées sur 4, 8 ou 16 bits selon la précision souhaitée et l'ordre de grandeur des données qui peuvent varier d'une étape de traitement à la suivante. Il est important d'adapter l'architecture des opérateurs arithmétiques en fonction des besoins et d'être capable de l'adapter temporairement en fonction de la précision du calcul souhaité. Ainsi en fixant la taille des représentations au plus juste nous pouvons réduire le temps de propagation, la surface et la consommation du circuit.Précision de calcul
La description structurelle du neurone en VHDL permet lors de la compilation de spécifier certaines caractéristiques telles que le nombre d'entrées et l'étendue des données en bits de façon générique, et de changer éventuellement le type des opérateurs arithmétiques : l'additionneur et le multiplieur. Le neurone effectue d'abord le produit des données en entrée, mémorisées dans une RAM avec les poids synaptiques correspondants lesquels sont dans une EEPROM puis il les additionne. Le résultat de ces opérations est soumis à une unité qui approxime une fonction d'activation par segment.Réalisation du neurone

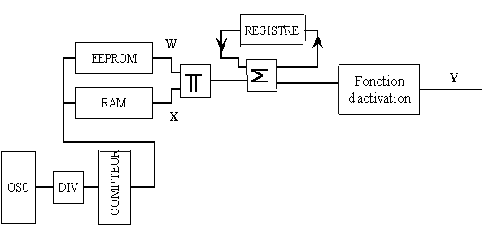
 Fig. architecture d'un neurone
Fig. architecture d'un neuroneOpérateurs arithmétiques

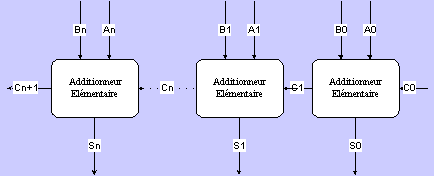
 Figure : Additionneur à retenue séquentielle
Figure : Additionneur à retenue séquentielle
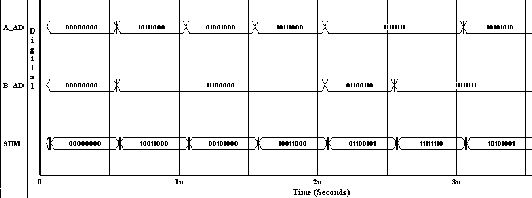
 Figure : Résultat de simulation d'un additionneur 8
bits
Figure : Résultat de simulation d'un additionneur 8
bits 
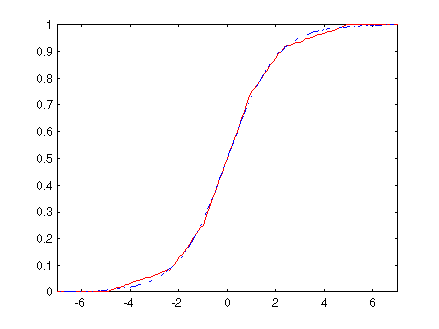
 Figure : La fonction sigmoïde et son approximation
Figure : La fonction sigmoïde et son approximation
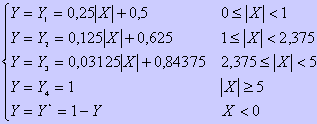

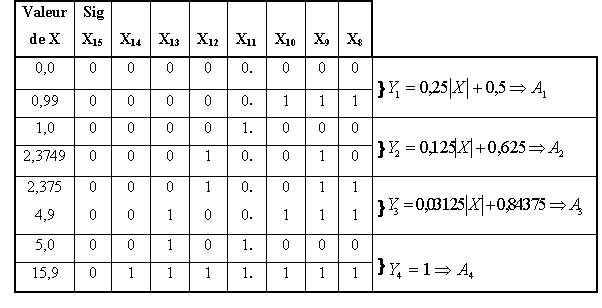

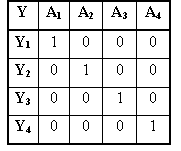

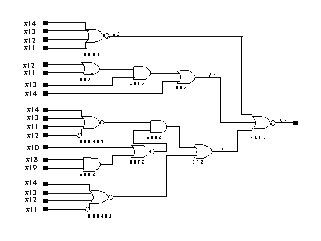
 Fig. comparateur d'amplitude
Fig. comparateur d'amplitude
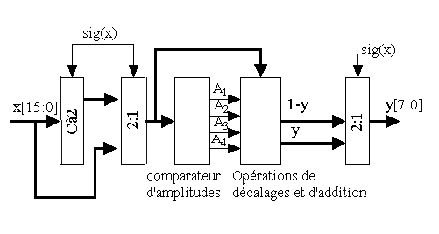
 Fig. implantation de la fonction sigmoïde
Fig. implantation de la fonction sigmoïdeLa description structurelle de la couche en VHDL permet lors de la compilation de spécifier le nombre de neurones sur la couche, cela nous donne la possibilité de synthétiser des couches à un nombre de neurones varié.Réalisation d'une couche

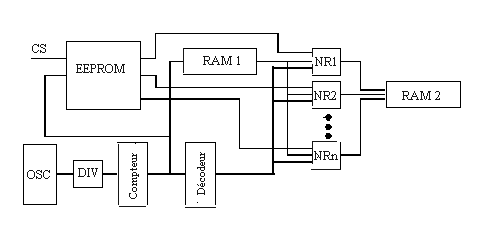
 Figure : Architecture d'une couche
Figure : Architecture d'une couche L'exploitation de la reconfiguration dynamique des circuits FPGA nous conduit à disposer de 2 RAM (RAM1 et RAM2) afin que les résultats issus du traitement de la couche de neurones (i - 1) soient traités par la couche de neurones suivante (i).Réalisation du réseau

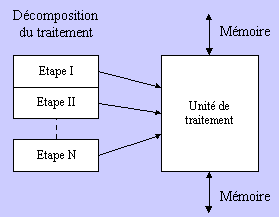
 Figure : synoptique du principe de la reconfiguration
dynamique
Figure : synoptique du principe de la reconfiguration
dynamique
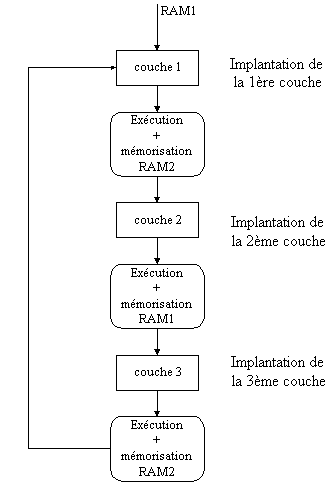

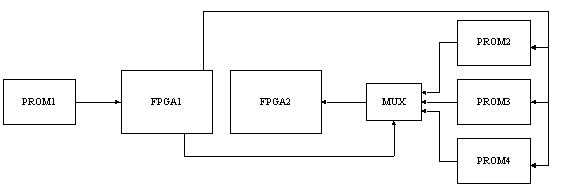
 Figure : schéma du couplage mémoire/FPGA
Figure : schéma du couplage mémoire/FPGA
Ce qu'il est important de noter c'est qu'on dispose dorénavant de très nombreuses possibilités d'exploiter des principes de mesure qui, a priori, sont inadaptés, dès lors qu'on a une bonne idée de ce qu'on veut obtenir et de ce que fournit réellement le capteur.
Mais, si l'on n'a aucune connaissance sur les défauts du capteur, il n'y aura pas de miracle, le traitement du signal aussi sophistiqué soit-il ne pourra vous venir en aide correctement
 |