
Copyright
© 2000-2015
LHERBAUDIERE
9 pages à l'impression

18 janvier 2014
 |
Copyright |
9 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 janvier 2014 |
| oscillateurs BF | les HF sont ailleurs | |||
| alimentation monotension | un schéma de référence | |||
| asservissement | juste une intro | |||
| une collection d'icônes pour visiter tout le site | ||||
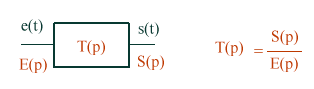
 (p)
= -
(p)
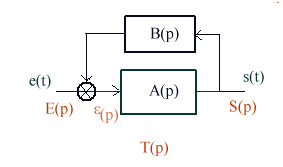
= - (p) soit E(p) = 0 et donc 1+A(p)B(p)
= 0 ce qui peut encore s'écrire |A(p)B(p)|=1
et Arg[A(p)B(p)]=p
(p) soit E(p) = 0 et donc 1+A(p)B(p)
= 0 ce qui peut encore s'écrire |A(p)B(p)|=1
et Arg[A(p)B(p)]=p
 selon le nombre d'étages) et la chaîne de retour doit être telle que B(p) soit
réel (quadripôle en général) pour la fréquence d'oscillation
selon le nombre d'étages) et la chaîne de retour doit être telle que B(p) soit
réel (quadripôle en général) pour la fréquence d'oscillation  0
telle que pour j
0
telle que pour j 0 = p la condition de Nyquist
soit vérifiée en faisant A > 1/|B(j
0 = p la condition de Nyquist
soit vérifiée en faisant A > 1/|B(j 0)|
0)|
Dans un oscillateur l'énergie destinée à compenser les inévitables pertes Joule est empruntée à une source continue. Cet apport d'énergie peut se faire de deux manières : soit au sein d'un composant dont la caractéristique courant tension comporte une région à résistance négative (par exemple une diode tunnel), soit le plus souvent en introduisant une réaction de la sortie sur l'entrée (ce que nous privilégions ici).Notons que si l'on fait B = -B la condition devient arg[AB] = 0
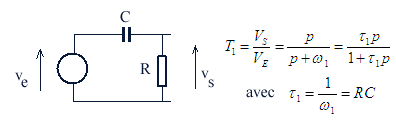 ou celui-ci
ou celui-ci 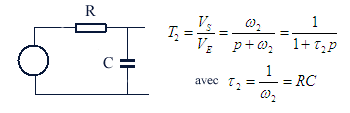
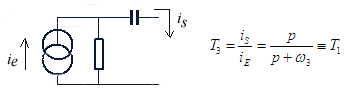 et
et 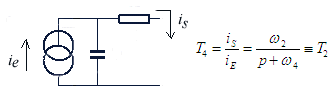
 /2,
il faudra donc en associer 3 en série pour obtenir un déphasage de
/2,
il faudra donc en associer 3 en série pour obtenir un déphasage de  ,
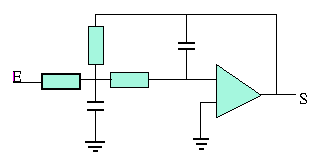
d'où le circuit à associer à un ampli_op:
,
d'où le circuit à associer à un ampli_op: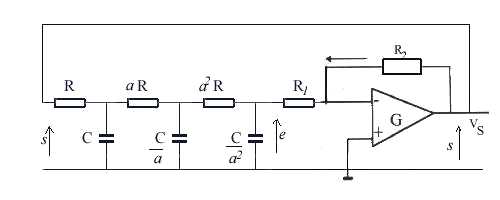
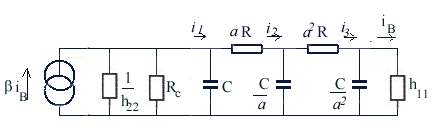
 ) la transmittance
de l'ensemble des 3 modules RC en série, le gain en boucle ouverte de l'ensemble
sera donc G(
) la transmittance
de l'ensemble des 3 modules RC en série, le gain en boucle ouverte de l'ensemble
sera donc G( ) = -B(
) = -B( )R2/R1.
Remarquons qu'en boucle fermée B(
)R2/R1.
Remarquons qu'en boucle fermée B( ) s'exprime
par s/e
) s'exprime
par s/e )
= 0 et donc B réel
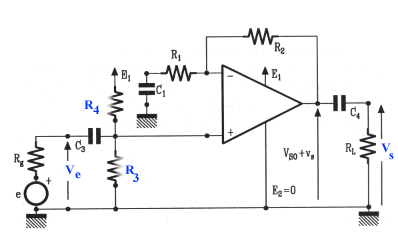
)
= 0 et donc B réel  ) en examinant le schéma
de ce quadripôle. On va considérer les diverses mailles en partant de la gauche.
On peut écrire un système de 4 équations dont la résolution permettra d'exprimer
vs/ve:
) en examinant le schéma
de ce quadripôle. On va considérer les diverses mailles en partant de la gauche.
On peut écrire un système de 4 équations dont la résolution permettra d'exprimer
vs/ve: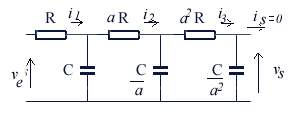 |
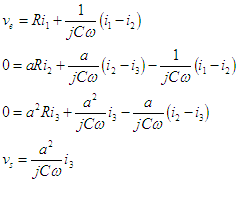 |
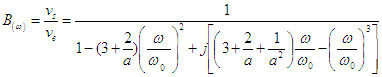 dans laquelle on a posé RC = 1/
dans laquelle on a posé RC = 1/ 0
0 ) soit réel il suffit donc d'annuler
le terme entre crochets j[ ] ce qui conduit à
) soit réel il suffit donc d'annuler
le terme entre crochets j[ ] ce qui conduit à  par la valeur d'oscillation
qu'on vient de calculer dans l'expression de G(
par la valeur d'oscillation
qu'on vient de calculer dans l'expression de G( )
on obtient
)
on obtient 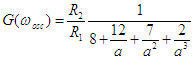 qui doit être >1 pour que la
seconde condition d'oscillation soit vérifiée. Il va de soi que cela ne pose
aucun problème.
qui doit être >1 pour que la
seconde condition d'oscillation soit vérifiée. Il va de soi que cela ne pose
aucun problème.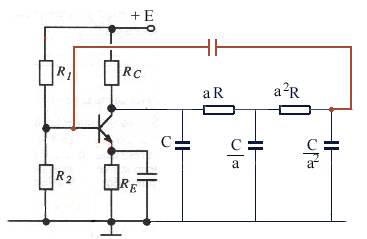
 ), un pont
de Wien dans la boucle de réaction, selon le schéma
suivant :
), un pont
de Wien dans la boucle de réaction, selon le schéma
suivant : 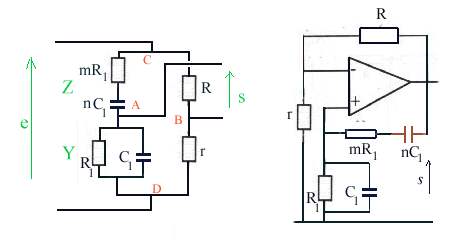
 )
soit nulle soit Imag(1+ZY) = 0 d'où l'on tire en posant R1C1
=
)
soit nulle soit Imag(1+ZY) = 0 d'où l'on tire en posant R1C1
= 1 que la fréquence
d'oscillation sera
1 que la fréquence
d'oscillation sera 
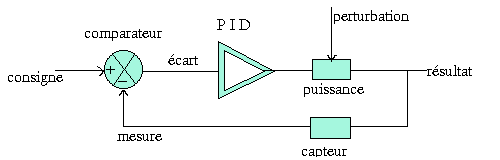
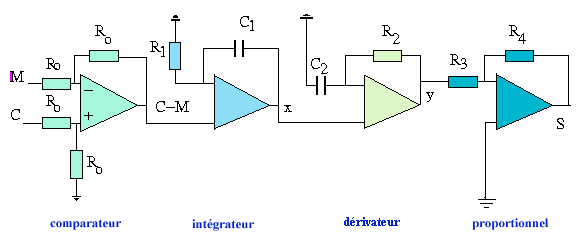
le premier est en fait le comparateur qui est chargé de faire la différence entre le signal mesuré M et la consigne C. Sa sortie sera donc E = C - M. |
le
quatrième étage, est un amplificateur de gain -
R4/R3 qui fournit donc une sortie proportionnelle
à son entrée S= - (R4/R3) y. |
le deuxième étage est du type intégrateur, il fournit une sortie x = (1 + 1/T1p))(C - M) où
p = j |
le troisième étage, du type dérivateur, produit y = (1 + T2 p) x avec T2 = R2C2 . L'utilité de ce montage est d'améliorer la vitesse de réponse en anticipant le passage à zéro de l'écart. |
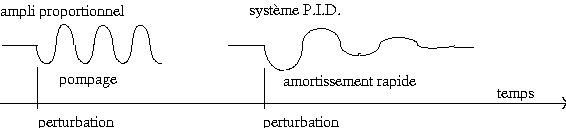
 |