
Copyright
© 2000-2015
LHERBAUDIERE
7 pages à l'impression

18 mars 2013
 |
Copyright |
7 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 18 mars 2013 |
Analyse des circuits 3/4
|
le
problème |
||||
|
une
idée géniale |
||||
|
les
principales |
||||
|
cas
particuliers bien utiles |
||||
|
à
mémoriser ou non |
||||
|
pour
savoir s'en servir |
||||
| une collection d'icônes pour visiter tout le site | ||||
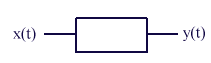
 +j
+j . On dira que F(p) est l'image de la fonction f(t)
laquelle sera appelée l'original. On note
parfois F(p) sous la forme
. On dira que F(p) est l'image de la fonction f(t)
laquelle sera appelée l'original. On note
parfois F(p) sous la forme 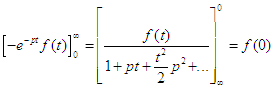 en conséquence
pF(p) = f(0) + F'(p)
en conséquence
pF(p) = f(0) + F'(p)| pn F(p) = F(n) (p) |
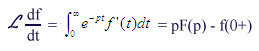 en faisant soit p tendant vers l'infini, soit p tendant vers zéro on
obtient les résultats ci-dessus
en faisant soit p tendant vers l'infini, soit p tendant vers zéro on
obtient les résultats ci-dessus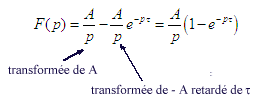
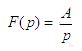
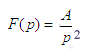
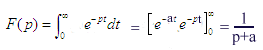
 ej
ej t
=jsin
t
=jsin t + cos
t + cos t et
on exprime à partir du résultat précédent que l'image
de ej
t et
on exprime à partir du résultat précédent que l'image
de ej t est 1/p-j
t est 1/p-j soit en séparant la partie imaginaire de la partie réelle on obtient
:
soit en séparant la partie imaginaire de la partie réelle on obtient
: 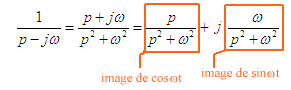
| image F(p) | original f(t) |
| A | |
| e-at | |
| t e-at | |
| at | |
| sinwt | |
| shwt | |
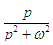 |
coswt |
| ch wt | |
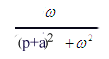 |
e-atsin wt |
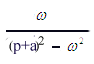 |
e-atsh wt |
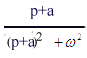 |
e-atcos wt |
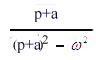 |
e-atchwt |
 et A1 = A e-j
et A1 = A e-j
 e(a+jb)t
+ Ae-j
e(a+jb)t
+ Ae-j e(a-jb)t = 2A
eat cos (bt+
e(a-jb)t = 2A
eat cos (bt+ )
)
Pour les éléments passifs RLC on a vu dans le premier chapitre les expressions fondamentales des courantsRésolvons donc notre système. La loi d'Ohm nous permet d'écrire u(t) = R i(t) + Ldi/dt équation différentielle très simple que l'on pourrait facilement résoudre par la méthode mathématique traditionnelle, mais il s'agit d'un exemple pédagogique et l'on va exploiter la transformée de Laplace. Les relations ci-dessus nous permettent d'écrire puisque u(t) = E que U(p) sera E/p on obtient donc aisément
u=Ri,,
la transformation de Laplace, dans chacun de ces éléments pris séparément, en se rappelant pF(p) = F'(p), conduit aux relations suivantes :
U(p) = R I(p), U(p) = Lp I(p) et I(p) = Cp U(p) d'où on tire les impédances dites opérationnelles R, Lp et 1/Cp. Notons que ces impédances opérationnelles s'expriment comme les impédances complexes si l'on remplace jpar p.
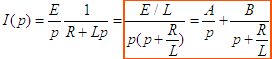
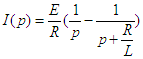
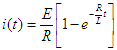
 |
 |