
Copyright
© 2000-2015
LHERBAUDIERE
5 pages à l'impression

18 mars 2013
 |
Copyright |
5 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 18 mars 2013 |
Analyse des circuits 2/4
|
le
signal alternatif |
||||
|
RLC |
||||
|
le
même mais différent! |
||||
|
une
boite noire |
||||
| une collection d'icônes pour visiter tout le site | ||||
 la phase. Dans
un circuit, tel celui ci-dessous, l'évolution de la tension aux bornes
de l'élément capacitif sera obtenue en résolvant l'équation
différentielle obtenue en appliquant la loi d'Ohm.
la phase. Dans
un circuit, tel celui ci-dessous, l'évolution de la tension aux bornes
de l'élément capacitif sera obtenue en résolvant l'équation
différentielle obtenue en appliquant la loi d'Ohm. 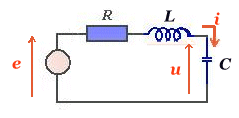
| soit
|
d'où on tire : |
| avec
|
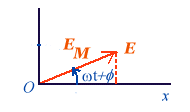
 et lorsque t croît on voit que le vecteur représentatif E
de cette fonction dans le plan complexe va simplement tourner autour
de 0 en conservant le même module de longueur EM.
et lorsque t croît on voit que le vecteur représentatif E
de cette fonction dans le plan complexe va simplement tourner autour
de 0 en conservant le même module de longueur EM.
Dans cette
représentation complexe les relations vues précédemment
et concernant les éléments passifs vont nous amener à la
notion d'impédance complexe.
résistance
: la loi d'Ohm u = Ri s'exprime dans le plan complexe par U = RI
avec U et I colinéaires de l'horizontale car R est une
quantité réelle, ce qui revient à dire qu'entre U
et I il n'y a aucun déphasage quel que soit t.
inductance : l'équation ![]() s'écrit maintenant U = jL
s'écrit maintenant U = jL I
et se représente graphiquement comme ci-dessous à gauche et l'on
voit que le vecteur tension est en avance sur le vecteur intensité
de
I
et se représente graphiquement comme ci-dessous à gauche et l'on
voit que le vecteur tension est en avance sur le vecteur intensité
de  /2. Rappelons que j est
un opérateur qui fait tourner la quantité qu'il multiplie de
/2. Rappelons que j est
un opérateur qui fait tourner la quantité qu'il multiplie de  /2
(et l'on a par conséquent j2 = -1, notons encore qu'on le
note parfois i en mathématiques et s dans les ouvrages en langue anglaise).
/2
(et l'on a par conséquent j2 = -1, notons encore qu'on le
note parfois i en mathématiques et s dans les ouvrages en langue anglaise).

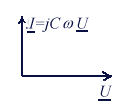
impédance
complexe d'une inductance
cas
d'une capacité
capacité
: l'équation ![]() s'écrit maintenant I = jC
s'écrit maintenant I = jC U
et se représente graphiquement comme ci-dessus à droite et l'on
voit dans ce cas que le vecteur tension est en retard de
U
et se représente graphiquement comme ci-dessus à droite et l'on
voit dans ce cas que le vecteur tension est en retard de  /2
sur le vecteur intensité.
/2
sur le vecteur intensité.
Le rapport
entre U et I s'appelle impédance
complexe et on le note généralement Z tandis
que son inverse sera l'admittance
Y
pour une
résistance
Z
= R
Y = 1/R
pour une
inductance
Z = jLw Y = 1/jLw
pour un
condensateur
Z = 1/jCw
Y = jCw
circuit
série
Ainsi la loi
d'Ohm dans notre circuit série ci-dessus va s'écrire dans le cas
d'un signal sinusoïdal sous forme d'une relation
algébrique
 - j/C
- j/C )
I = Z I
)
I = Z I
dans laquelle les modules de E et de I représenteront les valeurs
efficaces de la tension aux bornes du circuit et du courant le traversant.
En reprenant la notation de Fresnel on pourra exprimer l'impédance par
son module Z et un déphasage  déterminé par sa tangente
déterminé par sa tangente
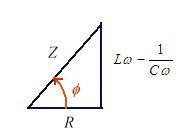
![]()
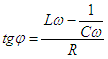
On remarquera évidemment que si la pulsation varie, tant le module que
le déphasage vont varier en fonction du terme ![]() .
Ainsi l'impédance va passer par un minimum lorsque ce terme sera nul
(dans ce cas Z = R et
.
Ainsi l'impédance va passer par un minimum lorsque ce terme sera nul
(dans ce cas Z = R et ![]() ),
c'est la résonance, et tendre vers zéro
lorsque
),
c'est la résonance, et tendre vers zéro
lorsque tendra vers zéro ou l'infini.
Parallèlement la phase passera par zéro pour
tendra vers zéro ou l'infini.
Parallèlement la phase passera par zéro pour  =
=  0, et tendra vers -
0, et tendra vers - /2
pour
/2
pour  tendant vers zéro et +
tendant vers zéro et + /2
pour l'infini.
/2
pour l'infini.
Notons enfin
qu'à la résonance la tension aux bornes de l'inductance pure est
très élevée et vaut L 0
U/R et on appelle facteur de surtension ou coefficient
de qualité la quantité Q = L
0
U/R et on appelle facteur de surtension ou coefficient
de qualité la quantité Q = L 0/R
(notion importante dans le chapitre sur le transistor en haute fréquence).
0/R
(notion importante dans le chapitre sur le transistor en haute fréquence).
circuit
parallèle : On exploite le principe
dit de dualité pour montrer que son étude se ramène
à la précédente à condition de remplacer U par I,
R par G et L par C
l'admittance s'exprime alors par ![]() ,
elle est minimale à la résonance pour laquelle dans la capacité
le courant est alors très élevé avec un facteur de surintensité
Q' = C
,
elle est minimale à la résonance pour laquelle dans la capacité
le courant est alors très élevé avec un facteur de surintensité
Q' = C 0/G
0/G
![]() On montre facilement que pour les fréquences, de part et d'autre de la
fréquence de résonance, correspondant à un déphasage
de 45° on a une amplitude de Z (circuit série) ou Y (circuit parallèle)
diminuée de moitié (soit exprimé en décibel
un affaiblissement de 3dB). Ces fréquences définissent ce qu'on
appelle communément la bande passante du
circuit .
On montre facilement que pour les fréquences, de part et d'autre de la
fréquence de résonance, correspondant à un déphasage
de 45° on a une amplitude de Z (circuit série) ou Y (circuit parallèle)
diminuée de moitié (soit exprimé en décibel
un affaiblissement de 3dB). Ces fréquences définissent ce qu'on
appelle communément la bande passante du
circuit .
![]()
Quadripoles
passifs :
On appelle
quadripole passif un ensemble de composants passifs que l'on va assimiler à
une boite noire comportant 2 bornes d'entrée et 2 bornes de sortie entre
lesquelles on pourra exprimer et éventuellement mesurer des quantités
significatives et utiles telles les courants et tensions d'entrée et
de sortie ainsi que les impédances équivalentes au dispositif
vu en entrée ou en sortie.
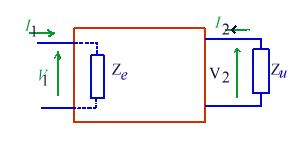
Ce quadripôle
étant passif, pour le choix des sens positifs des courants on prendra
la convention des récepteurs, c'est à dire les sens figurés
sur le schéma ci-dessus. Comme il est constitué d'éléments
linéaires (R, C et L non saturables) on peut écrire les lois des
mailles et après simplification on aboutira nécéssairement
à un couple de relations de la forme suivante:
On peut
montrer aisément que les impédances Z12 et Z21
sont égales. Notons enfin que si l'on avait choisi les conventions du
système générateur le signe + devant I2 serait changé
en - (mais bien évidemment le sens conventionnel choisi ne présume
en rien de la réalité physique du circuit qui est indépendante
des conventions).
V1 = Z11I1
+ Z12I2
V2 = Z21I1 + Z22I2
et bien entendu V2 = ZuI2
Toujours
en raison du principe de dualité on peut écrire les relations
du quadripôle en exprimant les admittances qui seront parfois plus adaptées
au problème examiné.
signification
des éléments :
I1 = Y11U1
+ Y12U2
I2
= Y21U1 + Y22U2
et Y12 = Y21
En faisant
des essais à vide ou en court circuit on peut identifier ces Z et Y .
Ainsi Z11 sera l'impédance d'entrée à vide
(c'est à dire lorsque les bornes de sorties sont ouvertes et que I2
est donc nul).
Z22
à l'inverse sera l'impédance de sortie à vide (I1
nul)
Z12= Z21 sera l'impédance de couplage (ou
impédance mutuelle)
Symétriquement Y11 sera l'admittance d'entrée de
court circuit (V2= 0), Y22 celle de sortie et Y12=
Y21 sera appelée admittance de transfert.
 |
 |