
Copyright
© 2000-2015
LHERBAUDIERE
5 pages à l'impression

18 mars 2013
 |
Copyright |
5 pages à l'impression |
 |
version initiale 2002 | |
| dernière
mise à jour 18 mars 2013 |
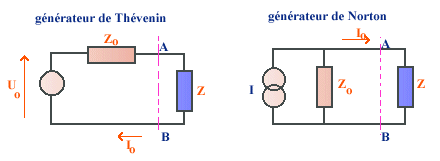
Analyse des circuits
|
Il n'était pas dans notre propos de faire un énième cours d'électronique et de théorie du signal, il en existe d'excellents, tant en librairie que sur le web et que nous avons répertoriés en bibliographie. Cependant dans un souci de cohérence et pour répondre aux demandes fréquentes de nos lecteurs nous avons décidé de présenter ici un minimum d'éléments d'information pour permettre au lecteur novice, ou à celui qui aurait oublié certaines bases, de mieux appréhender les différents chapitres de ce giga-site web. Ce module introductif sera donc découpé en trois grandes parties: une concernant les lois des réseaux et circuits linéaires, une seconde se rapportera aux signaux sinusoïdaux et assimilés, enfin nous présenterons la méthode d'analyse dite de Laplace qui, même si elle n'a plus les faveurs des théoriciens du signal, reste incontournable pour qui veut comprendre les méthodes de travail des électroniciens. |
|
les
dipôles classiques |
||||
|
une
décomposition courante |
||||
|
les
plus connus |
||||
|
les
noeuds et les mailles |
||||
|
étoile
ou triangle ? |
||||
|
base
de l'analyse en fréquence |
||||
| une collection d'icônes pour visiter tout le site | ||||
 |
 |
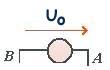
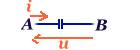
| U0 = VA-VB |
 |
 |
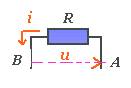
| résistance | inductance |
 |
défini
par la relation |
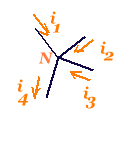 |
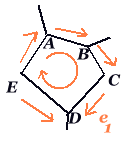 |
| noeud i1+ i2 + i3 - i4 = 0 | maille
|
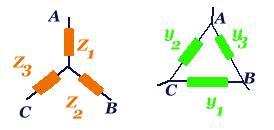
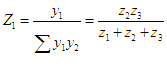 et inversement
que
et inversement
que 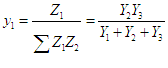 et de même
par permutation circulaire pour les autres grandeurs.
et de même
par permutation circulaire pour les autres grandeurs. |
 |