Copyright
© 2000-2015 LHERBAUDIERE


3 pages à l'impression		 Hit-Parade version initiale 2002
INFORMATION dernière mise à jour
18 mars 2013
cliquez sur le mot information pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives

Analyse des circuits 4/4

trouver la transformée de fonctions
du plus simple
trouver l'original connaissant l'image
  
étude de circuits
au plus compliqué
  une collection d'icônes pour visiter tout le site

Exercices sur la transformée de Laplace

Quelques exemples simples pour commencer : trouver la transformée des fonctions suivantes:

 

f(t) = 5 sin t la table donne directement

 

f(t) = 3( 1 - e-0,1t) = 3 - 3 e-0,1t réponse

 

f(t) = 5 cos [3t+ (p/4)] or cos(a+b )= cosa cosb - sina sinb
  et d'où
soit

Connaissant l'image trouver l'original

 on multiplie par p+3 les deux membres et fait p =-3
  d'où  
de même en multipliant par p+4 et faisant p=-4 on obtient B=-1
d'où
or soit :
ce qu'on va écrire F=F1+F2 pF(p) = f(0) +F'(p)
on identifie donc F2= 2F1/p c'est à dire que
d'où la première méthode possible  

On va d'abord décomposer F1, en déduire f1(t) puis on va intégrer 2f1(t), identifier f(0) pour finalement obtenir f(t)

Mais on peut aussi choisir une seconde méthode que nous allons examiner à titre pédagogique:

en exprimant que F1= pF2/2 en se rappelant toujours que pF(p) = f(0) +F'(p) avec toujours f(0) = lim pF(p) quand p tend vers l'infini. Ici on voit que f(0) =0. On en conclut donc que l'on pourra calculer f1(t) simplement en dérivant f2(t) et multipliant par 1/2 le résultat. On va donc calculer f2(t)

F2(p) = il vient facilement A=2/9 puis B=-2/10 qu'on remplace
on fait ensuite p=1 dans les deux membres,soit  
on fait alors p =2  

et l'on résoud ce système de 2 équations : Il vient C =-2/90 et D = -1/5 d'où

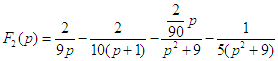 qui conduit à  
 
 
 
 
soit    

On pouvait bien évidemment mettre en oeuvre la troisième solution en écrivant directement et en exploitant la méthode vue ci-dessus; on obtient directement le résultat pour F(p) soit 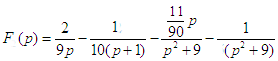et son original identique au résultat ci-dessus.

On notera que si les trois méthodes conduisent au même résultat final, c'est évidemment la troisième qui se révèle ici la plus rapide. Mais ce n'est pas toujours le cas.

étude de circuits

On donne le circuit ci-dessous alimenté à l'instant t=0 par une source continue E, on cherche la tension us(t) aux bornes de R2. On appellera Z l'impédance équivalente à l'ensemble C et R1 en parallèle.

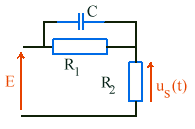
on a :

E = (Z + R2) i(t)

us(t) = R2 i(t)

 d'où
et

soit en remplaçant Z par son expression et en posant et

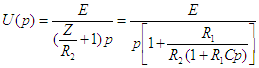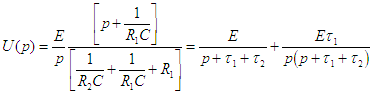en décomposant il vient :
d'où on tire et
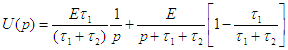soit u(t) d'après la table

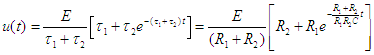Précisons que l'on aurait pu obtenir le même résultat en cherchant à déterminer I(p), puis i(t) et enfin u(t)=R2 i(t)