
Copyright
© 2000-2015
LHERBAUDIERE
8 pages à l'impression

18 mars 2013
 |
Copyright |
8 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
Introduction à l'automatique : systèmes asservis (1/3)
|
la boucle fermée
|
||||
|
réponse à un signal
|
||||
|
régimes et perturbations
|
||||
| une collection d'icônes pour visiter tout le site | ||||
chaîne fermée : notion d'asservissement linéaireintroduction
Dans les chapitres concernant les oscillateurs ou les filtres on a introduit la notion de système bouclé et celle de contre-réaction, nous allons généraliser ce concept à ce qu'on appelle les systèmes asservis et plus particulièrements aux asservissements linéaires qui sont évidemment un cas particulier plus simple à gérer que les asservissements non linéaires qui sont le cas général.
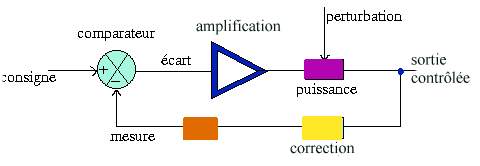
| un comparateur dont le rôle est de faire la différence entre la valeur mesurée de la grandeur que l'on veut asservir (c'est à dire la grandeur contrôlée à un coefficient multiplicateur près fonction du type de capteur mis en jeu) et la valeur, dite de consigne, que l'on voudrait obtenir. Le rôle de l'asservissement est évidemment de maintenir cette différence la plus proche possible de zéro à tout instant. |
| un amplificateur à plusieurs étages, généralement de type PID ou équivalent, chargé d'amplifier judicieusement l'écart mis en évidence par le comparateur afin d'apporter le plus rapidement possible une correction. |
| un étage de puissance qui est directement responsable de l'obtention de la grandeur pilotée. |
| un capteur chargé de mesurer en permanence la valeur de la grandeur asservie |
| un dispositif correcteur qui pourra être intégré en n'importe quel point de la chaîne (généralement là où c'est le plus facile), éventuellement dans l'amplificateur ou, comme sur ce schéma, dans la boucle de retour et destiné à améliorer le comportement d'ensemble en minimisant les oscillations susceptibles de se produire autour de la valeur de consigne. |
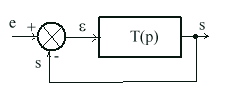 .
.
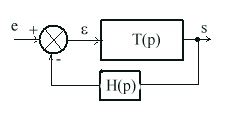 .
. = 0, ce n'est pas le cas dans un régulateur car c'est
= 0, ce n'est pas le cas dans un régulateur car c'est  qui engendre la grandeur de sortie. On peut d'ailleurs le montrer en représentant
le régulateur par un autre schéma équivalent au précédent
c'est-à dire un système à retour unitaire suivi en cascade
d'un bloc de transmittance 1/H(p).
qui engendre la grandeur de sortie. On peut d'ailleurs le montrer en représentant
le régulateur par un autre schéma équivalent au précédent
c'est-à dire un système à retour unitaire suivi en cascade
d'un bloc de transmittance 1/H(p).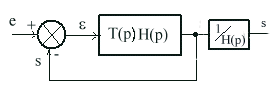
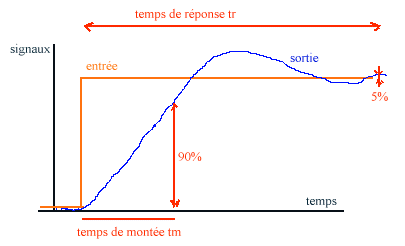
- tout d'abord le temps de montée tm , c'est le temps au bout duquel la sortie a atteint 90% de la valeur finale
- le premier dépassement : son amplitude ne doit pas dépasser de plus de 30% la valeur finale (50% étant généralement considéré comme prohibitif et souvent dangereux pour le dispositif). Notons que plus tm sera court et plus, généralement, le dépassement sera important.
- ce premier dépassement est suivi d'une évolution en forme de sinusoïde amortie
- le temps de réponse tr caractérise le temps mis par le système pour être stabilisé à plus ou moins 5% de la valeur finale, temps considéré comme correspondant sensiblement à la disparition du régime transitoire. On notera que ce temps est en corrélation avec l'importance du premier dépassement
- L'optimisation de la réponse d'un asservissement sera donc le meilleur compromis possible entre une montée rapide, un dépassement pas trop important (donc un amortissement important lequel augmente le temps de montée mais réduit le temps de réponse) et une fréquence propre d'oscillation non nuisible au système. Généralement ce compromis ne pourra être obtenu que par l'ajout de dispositifs correcteurs.
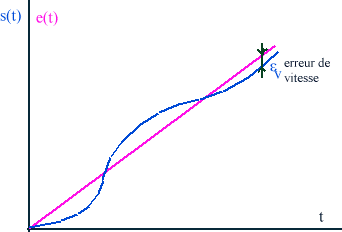
 V
encore appelée de manière plus imagée l'erreur de traînage.
V
encore appelée de manière plus imagée l'erreur de traînage.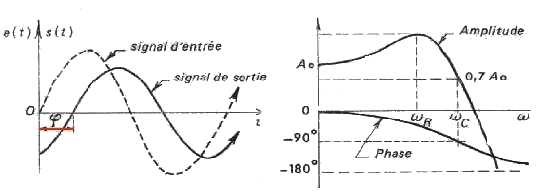
 . On dispose
en effet de deux représentations exploitables soit le diagramme
de Bode ci-dessus (à droite) qui exprime sur deux courbes séparées
d'une part l'amplitude et, d'autre part, la phase en fonction de la fréquence,
soit le diagramme de Nyquist (ci-dessous) qui concentre
l'ensemble des mêmes informations sur un unique diagramme dans le plan
complexe.
. On dispose
en effet de deux représentations exploitables soit le diagramme
de Bode ci-dessus (à droite) qui exprime sur deux courbes séparées
d'une part l'amplitude et, d'autre part, la phase en fonction de la fréquence,
soit le diagramme de Nyquist (ci-dessous) qui concentre
l'ensemble des mêmes informations sur un unique diagramme dans le plan
complexe.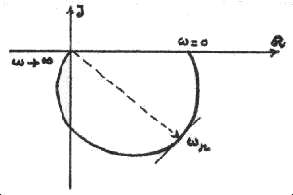
On va définir une
constante de position Kp = lim T(p) pour p = 0 constante de vitesse Kv = lim pT(p) pour p = 0 constante d'accélération Kg = lim p2T(p) pour p = 0
 p = lim
p = lim  (t)
quand t tend vers l'infini = lim p
(t)
quand t tend vers l'infini = lim p (p) quand p tend
vers zéro = lim E1/[1+KG(p)], soit
(p) quand p tend
vers zéro = lim E1/[1+KG(p)], soit  p
est nulle.
p
est nulle. (t) =
(t) =  1t.
Nous montrerons aisément que l'erreur de vitesse sera non nulle pour
un système de type 1, infinie pour un système de type 0, mais
nulle pour tout système ayant a > 1
1t.
Nous montrerons aisément que l'erreur de vitesse sera non nulle pour
un système de type 1, infinie pour un système de type 0, mais
nulle pour tout système ayant a > 1 1/p2
1/p2 v = lim
v = lim  (t)
= lim p
(t)
= lim p  (p) = lim
(p) = lim  1/[p+pKG(p)]
=
1/[p+pKG(p)]
=  1/Kv or Kv vaut
0 pour a = 0, K pour a = 1 et l'infini pour a > 1
1/Kv or Kv vaut
0 pour a = 0, K pour a = 1 et l'infini pour a > 1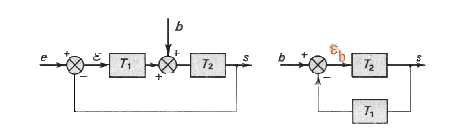
 pb
= lim
pb
= lim  (t)
pour t infini = lim p
(t)
pour t infini = lim p (p) pour p tendant vers zéro
= B1lim W/T1
(p) pour p tendant vers zéro
= B1lim W/T1 pb
= 0 et il n'y a aucune erreur de position.
pb
= 0 et il n'y a aucune erreur de position. pb
est B1/K1; si T2 ne possède pas d'intégration,
la limite est
pb
est B1/K1; si T2 ne possède pas d'intégration,
la limite est  pb = B1/[K1+1/K2].
Dans les deux cas il y a erreur de position.
pb = B1/[K1+1/K2].
Dans les deux cas il y a erreur de position. ))
et l'on va examiner essentiellement la stabilité, en remarquant qu'un
système asservi est stable si le polynôme 1+KG(p) = 0 ne possède
pas de racines dans la partie droite du plan complexe ni sur l'axe imaginaire,
en d'autres termes si ses zéros sont dans la partie gauche. C'est cette
propriété que précise graphiquement le critère
du revers qui s'énonce : un système linéaire est stable
si, en décrivant le lieu de transfert en boucle ouverte dans le sens
des fréquences croissantes, on laisse le point critique -1+ j0 à
sa gauche.
))
et l'on va examiner essentiellement la stabilité, en remarquant qu'un
système asservi est stable si le polynôme 1+KG(p) = 0 ne possède
pas de racines dans la partie droite du plan complexe ni sur l'axe imaginaire,
en d'autres termes si ses zéros sont dans la partie gauche. C'est cette
propriété que précise graphiquement le critère
du revers qui s'énonce : un système linéaire est stable
si, en décrivant le lieu de transfert en boucle ouverte dans le sens
des fréquences croissantes, on laisse le point critique -1+ j0 à
sa gauche.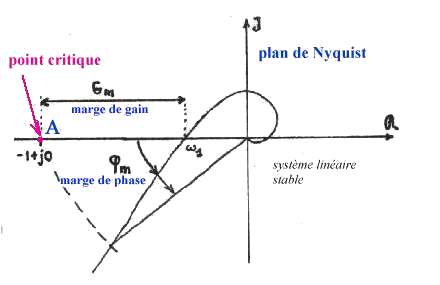
 )| pour
)| pour
 =
=  1
).
1
). |
 |