
Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression

18 mars 2013
 |
Copyright |
6 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
Introduction à l'automatique : asservissements (2/3)
| méthodes de correction des SA | les classiques | |||
| PID pratique | tout en un | |||
| systèmes non linéaires | juste une intro | |||
| une collection d'icônes pour visiter tout le site | ||||
 )
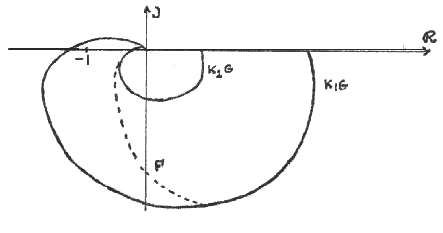
possédant une phase positive dans la région de la résonance.
On peut ainsi introduire un facteur dérivé de la forme J(p)
= 1+
)
possédant une phase positive dans la région de la résonance.
On peut ainsi introduire un facteur dérivé de la forme J(p)
= 1+ p dont le lieu de transfert est une demi-droite
et l'avance de phase réalisée à la résonance (
p dont le lieu de transfert est une demi-droite
et l'avance de phase réalisée à la résonance ( )
est arctgt
)
est arctgt . Pratiquement il est impossible d'obtenir
un tel facteur dérivé avec un réseau passif et l'on se
contentera d'un facteur d'avance de phase dont la fonction de transfert est
de la forme
. Pratiquement il est impossible d'obtenir
un tel facteur dérivé avec un réseau passif et l'on se
contentera d'un facteur d'avance de phase dont la fonction de transfert est
de la forme  p.
p.
 la constante de
temps du réseau. L'avance de phase maximale correspond à
la constante de
temps du réseau. L'avance de phase maximale correspond à 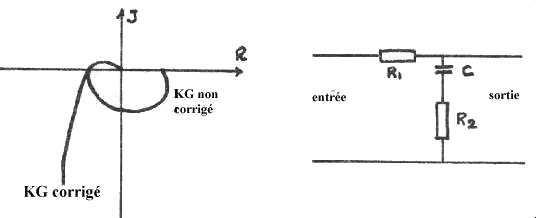
 p
dans la branche de retour, tel qu'une dynamo tachymétrique
branchée sur l'arbre de sortie du moteur.
p
dans la branche de retour, tel qu'une dynamo tachymétrique
branchée sur l'arbre de sortie du moteur.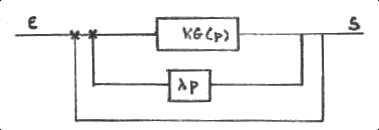

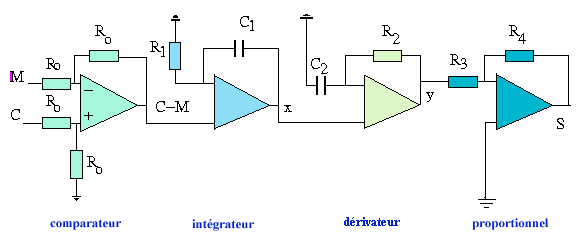
 et T1 = R1C1 est la constante de temps
de l'intégrateur. Cet étage permet d'augmenter sensiblement la réponse quand
l'écart est important et garantit un écart nul en régime stable, ce que
l'on ne peut obtenir avec un seul étage proportionnel.
et T1 = R1C1 est la constante de temps
de l'intégrateur. Cet étage permet d'augmenter sensiblement la réponse quand
l'écart est important et garantit un écart nul en régime stable, ce que
l'on ne peut obtenir avec un seul étage proportionnel.
 t et
l'on recueille à l'autre extrémité de la coupure s = s0sin(
t et
l'on recueille à l'autre extrémité de la coupure s = s0sin( t+j)
ce qui pour chaque fréquence permet de déterminer l'amplitude
A = s0/e0 et la phase f de
KG(j
t+j)
ce qui pour chaque fréquence permet de déterminer l'amplitude
A = s0/e0 et la phase f de
KG(j ) puis de tracer dans le plan de Nyquist
le lieu représentatif de la fonction de transfert. Grâce aux propriétés
de linéarité A et f sont fonction de la fréquence et non
de l'amplitude d'entrée.
) puis de tracer dans le plan de Nyquist
le lieu représentatif de la fonction de transfert. Grâce aux propriétés
de linéarité A et f sont fonction de la fréquence et non
de l'amplitude d'entrée. t.
Cette sortie est en général périodique
mais non sinusoïdale, c'est pourquoi on définit par convention
une fonction sinusoïdale s1(t) = s0sin(
t.
Cette sortie est en général périodique
mais non sinusoïdale, c'est pourquoi on définit par convention
une fonction sinusoïdale s1(t) = s0sin( t+
t+ )
que l'on qualifie d'équivalent à s(t) et qui permet de définir
une fonction de transfert équivalente. Pour s1(t) on prend
généralement le premier harmonique de s(t).
)
que l'on qualifie d'équivalent à s(t) et qui permet de définir
une fonction de transfert équivalente. Pour s1(t) on prend
généralement le premier harmonique de s(t). mais aussi de l'amplitude
d'entrée e0. On n'a plus un lieu de transfert mais une famille
de lieux de transfert, un par amplitude d'entrée.
mais aussi de l'amplitude
d'entrée e0. On n'a plus un lieu de transfert mais une famille
de lieux de transfert, un par amplitude d'entrée.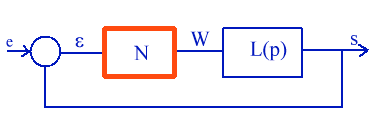
 )
gradué en fréquence, les organes non linéaires caractérisés,
dans le cadre de l'approximation du premier harmonique, par leur lieu critique
-1/N(
)
gradué en fréquence, les organes non linéaires caractérisés,
dans le cadre de l'approximation du premier harmonique, par leur lieu critique
-1/N( 1) gradué en amplitude.
La fonction de transfert généralisée en boucle ouverte
apparaît ainsi comme un produit N(
1) gradué en amplitude.
La fonction de transfert généralisée en boucle ouverte
apparaît ainsi comme un produit N( 1)L(j
1)L(j )
dont le premier facteur caractérisant l'élément non linéaire
est fonction de l'amplitude seule et le second caractérisant les éléments
linéaires est fonction de la fréquence seule.
)
dont le premier facteur caractérisant l'élément non linéaire
est fonction de l'amplitude seule et le second caractérisant les éléments
linéaires est fonction de la fréquence seule. ) parcouru dans
le sens des fréquences croissantes laisse le point critique -1/K à
sa gauche. Cette propriété peut s'étendre aux systèmes
non linéaires. Lorsque
) parcouru dans
le sens des fréquences croissantes laisse le point critique -1/K à
sa gauche. Cette propriété peut s'étendre aux systèmes
non linéaires. Lorsque  1
est constant N(
1
est constant N( 1) est un nombre
fixe et on peut assimiler le système à un système linéaire
de fonction de transfert N(
1) est un nombre
fixe et on peut assimiler le système à un système linéaire
de fonction de transfert N( 1)L(p).
Le système est stable pour l'amplitude
1)L(p).
Le système est stable pour l'amplitude  1
si le lieu de transfert laisse à sa gauche le point critique.
1
si le lieu de transfert laisse à sa gauche le point critique. 1
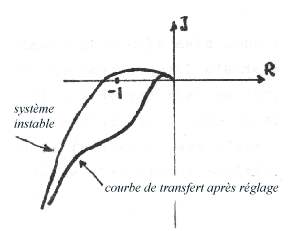
(ou quelle gamme d'amplitude). Et, comme pour les systèmes linéaires,
on pourra améliorer les performances à l'aide de correcteurs de
compensation.
1
(ou quelle gamme d'amplitude). Et, comme pour les systèmes linéaires,
on pourra améliorer les performances à l'aide de correcteurs de
compensation.
 |
 |