
Copyright
© 2000-2015
LHERBAUDIERE
8 pages à l'impression

18 mars 2013
 |
Copyright |
8 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
Introduction à l'automatique : asservissements (3/3)
| microbalance de torsion | expression de la sensibilité | |||
| le servomécanisme | description et étude | |||
| la stabilité | les résultats | |||
| une collection d'icônes pour visiter tout le site | ||||
Position du problèmeAfin d'illustrer la notion d'asservissement nous allons décrire la réalisation d'une microbalance de torsion électroniquement asservie, dispositif réalisé dans les années soixante au laboratoire de physique électronique de l'INSCI Rouen par J. Gouault et M. Hubin, mais qui présente de nombreux intérêts pédagogiques.
Ce dernier type présente cependant l'avantage de pouvoir fonctionner en méthode de zéro ce qui est toujours un gage de grande précision. On compense en effet la déflexion due à la charge par une force de type magnétique ou électromagnétique donc aisément modulable. Compte tenu de l'objectif visé ici, mesure de très faibles masses dans le domaine des microgrammes, nous avons choisi une compensation électrostatique qui met en jeu des forces éventuellement très faibles, mais permet un asservissement à stabilité de zéro.
- les balances de flexion constituées d'un bras horizontal fixé en une extrémité et qui fléchit sous l'effet d'une charge placée à l'autre extrémité.
- les balances à ressort spiral consistant en une variante plus sensible du type précédent et constituée le plus souvent d'un ressort de quartz s'étirant sous la charge.
- les balances à couteaux, dérivées des balances analytiques classiques, peu précises et inadaptées au milieu de vide.
- les balances à pivots, trop fragiles
- les balances de torsion admettant des charges supérieures à celles à ressort de quartz, mais cependant aussi fragiles et souffrant des mêmes inconvénients, à savoir une sensibilité aux vibrations et à la température.
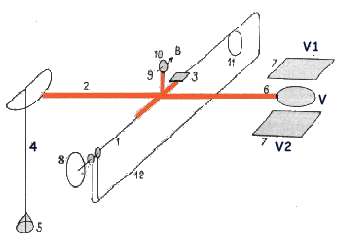 |
1 fil
de torsion en tungstène 20µm de diamètre |
 V et
z = dz + e/2 soit
V et
z = dz + e/2 soit 
 s'exprime comme le rapport de l'angle de rotation d
s'exprime comme le rapport de l'angle de rotation d du fléau à la masse dm de la surcharge déposée
du fléau à la masse dm de la surcharge déposée  = d
= d /dm
/dm
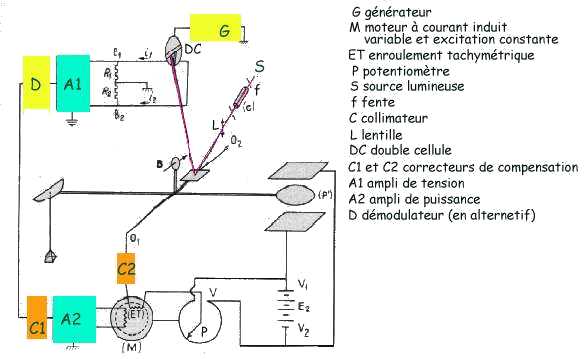
 et le poids de la nacelle et de sa charge est
appliqué en O'1 tandis que la force électrostatique
est appliquée en O'2. Dans ces conditions la sensibilité
s'exprime par la relation
et le poids de la nacelle et de sa charge est
appliqué en O'1 tandis que la force électrostatique
est appliquée en O'2. Dans ces conditions la sensibilité
s'exprime par la relation
 V0.
La mesure de
V0.
La mesure de  V0
permet de connaitre la masse déposée.
V0
permet de connaitre la masse déposée.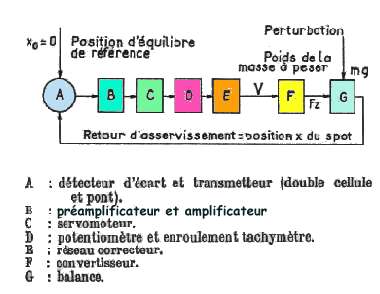
 = x0-x, l'amplificateur A2
délivre à sa sortie une tension U. En admettant une constante
de temps égale à T1, il vient en transformée
de Laplace
= x0-x, l'amplificateur A2
délivre à sa sortie une tension U. En admettant une constante
de temps égale à T1, il vient en transformée
de Laplace  d
d /dt
la fem prenant naissance dans l'induit;
/dt
la fem prenant naissance dans l'induit;  angle de rotation du moteur; R résistance de l'induit.
angle de rotation du moteur; R résistance de l'induit. posons
posons
 > 1
> 1  = T on obtient
= T on obtient 
 , on a
l = k'3
, on a
l = k'3 on peut donc
écrire que
on peut donc
écrire que  V est proportionnel
à
V est proportionnel
à  soit finalement
soit finalement 
 l'angle de rotation supposé petit; V+ldV/dt la somme des tensions délivrées
par le curseur du potentiomètre et l'enroulement tachymétrique.
L'équation différentielle du mouvement du fléau s'exprime
par
l'angle de rotation supposé petit; V+ldV/dt la somme des tensions délivrées
par le curseur du potentiomètre et l'enroulement tachymétrique.
L'équation différentielle du mouvement du fléau s'exprime
par  V2
devant (V1-V2)2 puisque expérimentalement
nous opérerons avec
V2
devant (V1-V2)2 puisque expérimentalement
nous opérerons avec  V
petit devant V1-V2. On a dz = l2
V
petit devant V1-V2. On a dz = l2
 soit
soit
 on obtient
on obtient 
 V0
= -gl1m/k2 ce qu'on avait démontré
au début.
V0
= -gl1m/k2 ce qu'on avait démontré
au début. Ve
=
Ve
=  V0cos
V0cos t
et on récupérera
t
et on récupérera  V0
|KG(p)|cos(
V0
|KG(p)|cos( t+
t+ )
en sortie de l'enroulement
)
en sortie de l'enroulement 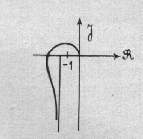 |
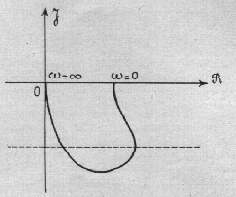 |
| courbe1: B1(jw) | courbe 2 : B2(jw)C(jw) |
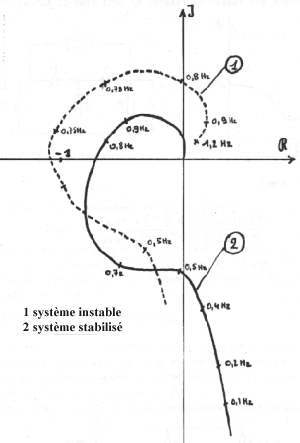
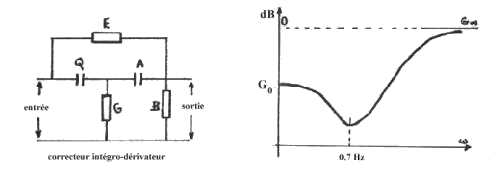
Il est bon de savoir que pour tracer aisément le lieu de Nyquist il existe des appareils appelés transféromètres permettant de générer le signal V0cos
t et de mesurer la phase et l'amplitude résultantes à l'autre bout de la coupure (ou en tout point accessible du système en boucle ouverte) sur une plage étendue de fréquences (d'une fraction de Hertz à quelques centaines de KHz si besoin est).
 |