 |
Copyright |
9 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 22 mars 2013 |
 |
Copyright |
9 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 22 mars 2013 |
troisième partie (3/7)
| oscillateurs : généralités | le système bouclé | |||
| oscillateurs HF : les concepts | Hartley, Colpitts, Clapp... | |||
| stabilité d'un oscillateur | glissement de F et dérives | |||
| synthétiseur de fréquence | direct, indirect ou numérique | |||
| une collection d'icônes pour visiter tout le site |
||||
Un oscillateur est un système bouclé. Nous rappelons ci-dessous quelques éléments.généralités
système bouclé

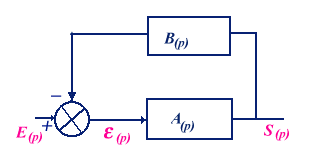
Un oscillateur est un amplificateur capable de délivrer un signal de sortie sinusoïdal en l'absence de signal d'entrée. Ceci étant possible grâce à un couplage entre sortie et entrée de telle sorte que la fraction du signal de sortie qui est réinjectée à l'entrée soit responsable d'un signal de sortie d'amplitude au moins égale à celle qui lui a donné naissance soit E(p) - e(p) = -e(p) d'où E(p) = 0, ce qui revient à écrire la condition 1+ A(p)B(p) = 0 soit encore |A(p)B(p)| = 1 et Arg[A(p)B(p)] = p.condition d'oscillation
En pratique la chaîne directe est constituée d'un étage amplificateur à transistor ou à amplificateur opérationnel générant argA = 0 ou p selon le nombre d'étages, et la chaîne de retour doit être telle que B(p) soit réel (quadripôle en général) pour la fréquence d'oscillationstructure d'un oscillateur sinusoïdal
 o telle que pour j
o telle que pour j o
=
o
=  la condition de Nyquist
soit vérifiée. On choisira A > 1/|B(j
la condition de Nyquist
soit vérifiée. On choisira A > 1/|B(j o)|.
o)|.oscillateurs HF

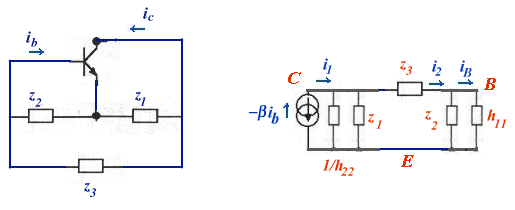
 ib
(si 1/h22 est grand) d'où
ib
(si 1/h22 est grand) d'où 
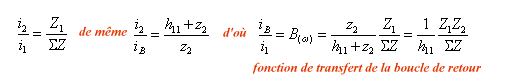

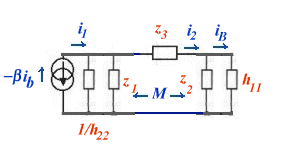


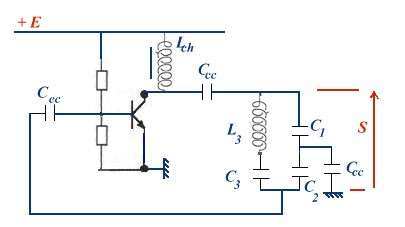
C'est un oscillateur sans inductance mutuelle dans lequel z1 et z2 sont des capacités et z3 un circuit LC sérieoscillateur de Clapp


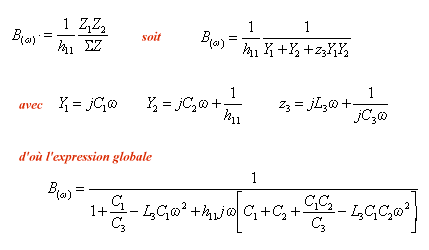
 o)
soit réel cela signifie donc que la partie imaginaire de B(
o)
soit réel cela signifie donc que la partie imaginaire de B( )
doit être nulle à la fréquence d'oscillation ce qui revient
dans l'expression ci-dessus à annuler le terme entre crochets
)
doit être nulle à la fréquence d'oscillation ce qui revient
dans l'expression ci-dessus à annuler le terme entre crochets
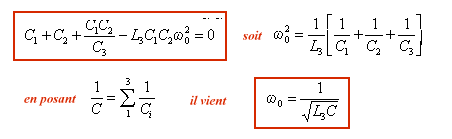
 )
)
 o par sa valeur il vient B(
o par sa valeur il vient B( o)
= - C2/C1
o)
= - C2/C1 iB
le gain en boucle fermée sera donc -
iB
le gain en boucle fermée sera donc -  B
et la condition sur le gain est donc que
B
et la condition sur le gain est donc que  C2/C1
> 1 ce qui ne présente pas de difficulté pratique
de réalisation.
C2/C1
> 1 ce qui ne présente pas de difficulté pratique
de réalisation.
C'est une variante du précédent dans lequel z3 est constitué soit d'une simple inductance, et dans ce cas les résultats sont identiques : il suffit de supprimer C3 dans les relations précédentes, soit on remplace z3 par un quartz piézoélectrique dont le facteur de qualité est très supérieur à ce qu'on peut espérer d'un circuit LC (on obtient très aisément Q > 3000).oscillateur de Colpitts

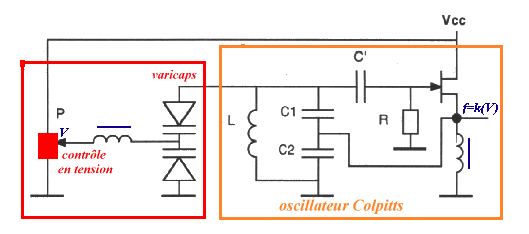
 Fig.
oscillateur de Colpitts contrôlé en tension
Fig.
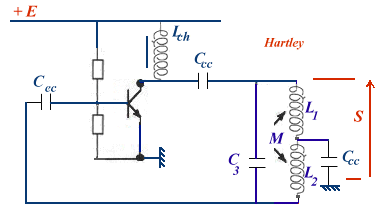
oscillateur de Colpitts contrôlé en tensionDans ce cas z1 et z2 sont des inductances tandis que z3 est de type capacitif et on aura une inductance mutuelle.oscillateur Hartley


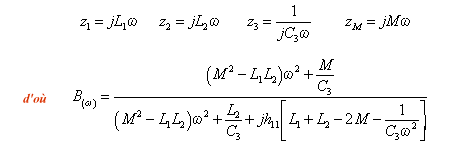
 o) réel conduit à
o) réel conduit à 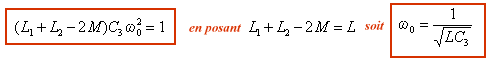
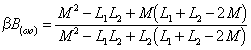 soit supérieur à 1.
soit supérieur à 1.
L'amplificateur idéal devrait fournirstabilité des oscillateurs
 o et une
amplitude So constants quelles que soient la charge et les conditions
de fonctionnement. En fait la fréquence résulte des éléments
du montage et toute variation de ceux-ci entrainera un glissement de fréquence
et une dérive d'amplitude.
o et une
amplitude So constants quelles que soient la charge et les conditions
de fonctionnement. En fait la fréquence résulte des éléments
du montage et toute variation de ceux-ci entrainera un glissement de fréquence
et une dérive d'amplitude.
L'idée de base est de partir d'un oscillateur à quartz de haute stabilité et simultanément d'en diviser et multiplier la fréquence via deux circuits indépendants et ensuite de mélanger ces deux fréquences et de filtrer le résultat par un filtre passe-haut. Le schéma de principe est le suivant.synthèse directe

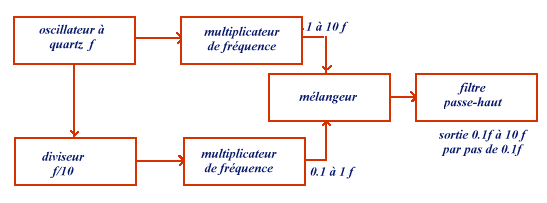
 fig.
synthèse de fréquence directe
fig.
synthèse de fréquence directeOn exploite ici encore un oscillateur à quartz pour une référence de stabilité et on l'associe selon le principe ci-dessous à un oscillateur contrôlé en tension (VCO). Le VCO par principe délivre une fréquence directement fonction de la tension de commande. L'idée est d'asservir astucieusement la fréquence du VCO à celle du quartz à un coefficient multiplicateur près, lequel peut être aisément modifié.synthèse indirecte

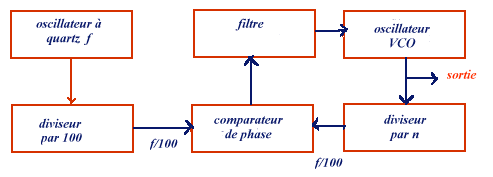
 Fig. princioe
de la synthèse de fréquence indirecte
Fig. princioe
de la synthèse de fréquence indirecteLa dernière technologie de synthèse de fréquence repose sur l'utilisation de techniques numériques directes. Le principe est d'exploiter le principe du convertisseur numérique analogique piloté par un programme. En effet si l'on envoie à l'entrée d'un CNA une information digitale suivant dans le temps une évolution de type sinusoïdale la sortie du CNA va fournir un signal analogique sensiblement sinusoïdal (en fait en marche d'escalier dont l'enveloppe serait une sinusoïde) qu'il suffira de faire transiter par un filtre relativement simple pour lisser le signal et obtenir une presque parfaite sinusoïdesynthèse numérique

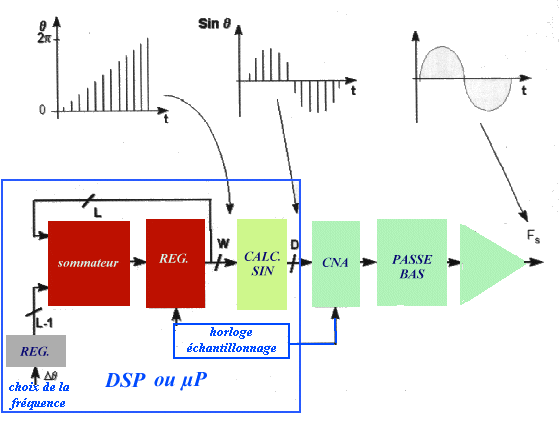
 fig.
synthèse numérique directe
fig.
synthèse numérique directe , typiquement ce sera une
table de correspondance en ROM interne au processeur (LUT look up table)
, typiquement ce sera une
table de correspondance en ROM interne au processeur (LUT look up table)
 |