
Copyright
© 2000-2015
LHERBAUDIERE
8 pages à l'impression

18 mars 2013
 |
Copyright |
8 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
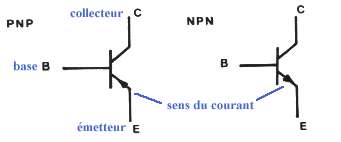
TRANSISTORS
première partie (1/3) transistor
bipolaire
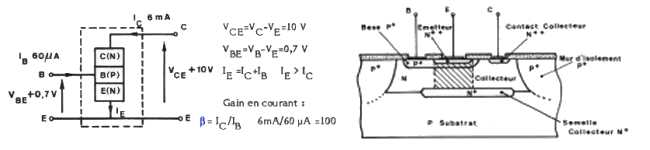
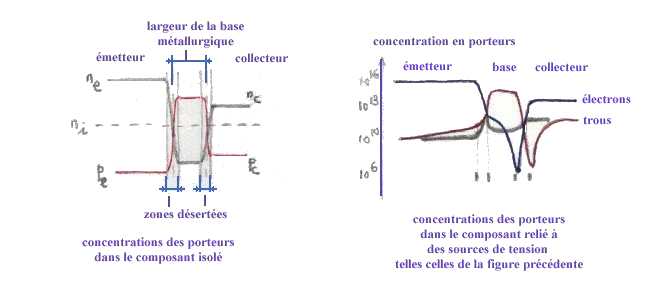
| principe et fonctionnement | deux jonctions opposées | |||
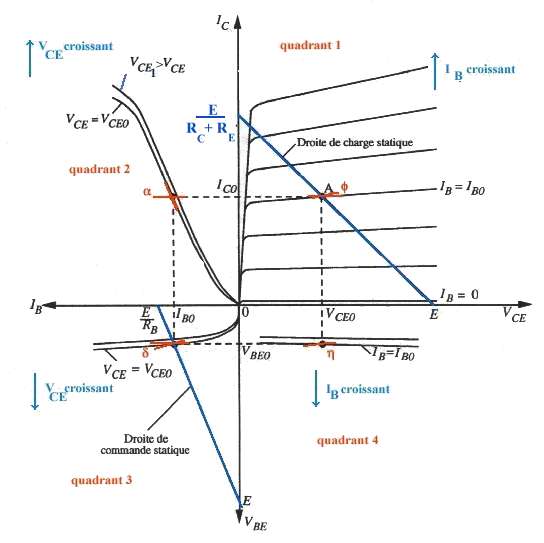
| caractéristiques statiques | Ebers et Moll | |||
| rôle de la température | la dérive d'Icb0 | |||
| amplificateur de faibles signaux | et de moyenne fréquence | |||
| schéma équivalent dynamique | le quadripole pratique | |||
| une collection d'icônes pour visiter tout le site |
||||
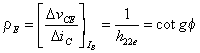 représente la résistance de sortie
du transistor
représente la résistance de sortie
du transistor 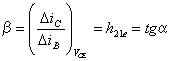 est le coefficient d'amplification en courant
est le coefficient d'amplification en courant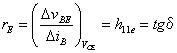 est la résistance d'entrée du transistor
est la résistance d'entrée du transistor
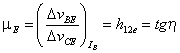 est le coefficient de réaction dont le graphique
montre qu'il est sensiblement nul dans ce cas.
est le coefficient de réaction dont le graphique
montre qu'il est sensiblement nul dans ce cas.  constant).
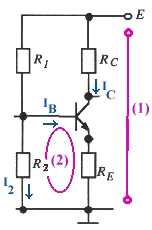
constant).  IB et lorsque
la température augmente ICB0 augmente ce qui se traduit par
un décalage vers le haut de l'ensemble des courbes et une perturbation
globale du fonctionnement du transistor, c'est à dire un décalage
du point de fonctionnement et donc une dérive de l'ensemble des caractéristiques
du montage dans lequel est intégré ce transistor, ce qui est inacceptable
en particulier en métrologie.
IB et lorsque
la température augmente ICB0 augmente ce qui se traduit par
un décalage vers le haut de l'ensemble des courbes et une perturbation
globale du fonctionnement du transistor, c'est à dire un décalage
du point de fonctionnement et donc une dérive de l'ensemble des caractéristiques
du montage dans lequel est intégré ce transistor, ce qui est inacceptable
en particulier en métrologie.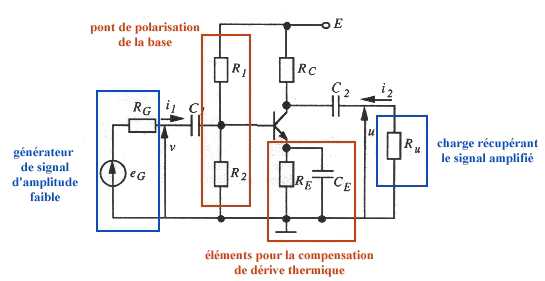
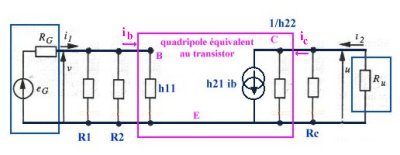
 IB
soit sensiblement
IB
soit sensiblement  IB.
IB.| v1 = h11 i1 + h12 v2 |
| i2 = h21 i1 + h22 v2 |
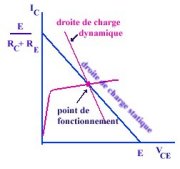
 ...
...
 |
 |