
Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression

18 mars 2013
 |
Copyright |
6 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
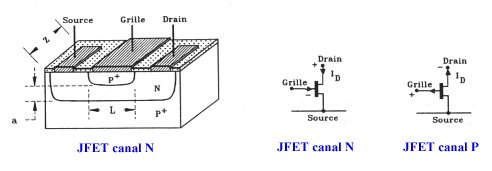
TRANSISTORS
deuxième partie (2/3) : transistor à effet
de champ
| principe et fonctionnement | un canal plus ou moins ouvert | |||
| équations du TEC | dans la zone centrale | |||
| caractéristiques | ||||
| mise en oeuvre schéma équivalent | le montage source commune | |||
| applications typiques | l'étage d'entrée | |||
| une collection d'icônes pour visiter tout le site |
||||
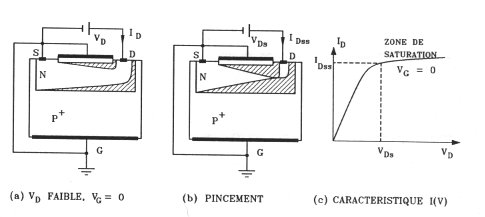
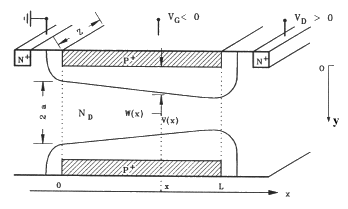
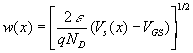
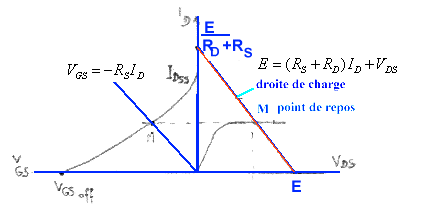
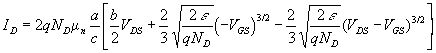 relation entre ID,
VDS et VGS que l'on exploite en traçant les caractéristiques
(voir courbes ci-avant) ID = f(VDS) à VGS
constante. L'analyse de cette équation montre que lorsque VDS
augmente ID va d'abord croitre puis atteindre un maximum pour VDS
= Vp, dite tension de pincement,
au delà de laquelle la réduction de largeur du canal compense
l'augmentation de courant liée à l'augmentation de VDS.
relation entre ID,
VDS et VGS que l'on exploite en traçant les caractéristiques
(voir courbes ci-avant) ID = f(VDS) à VGS
constante. L'analyse de cette équation montre que lorsque VDS
augmente ID va d'abord croitre puis atteindre un maximum pour VDS
= Vp, dite tension de pincement,
au delà de laquelle la réduction de largeur du canal compense
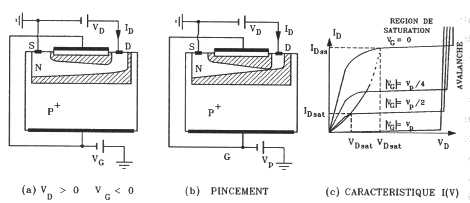
l'augmentation de courant liée à l'augmentation de VDS.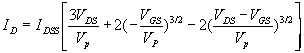 d'où l'on tire le courant maximal correspondant à VDS-
VGS= Vp
d'où l'on tire le courant maximal correspondant à VDS-
VGS= Vp 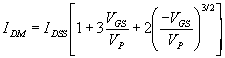 pour VGS > VGSoff on constate que IDM = 0.
Il ne faut donc pas polariser trop négativement la grille.
pour VGS > VGSoff on constate que IDM = 0.
Il ne faut donc pas polariser trop négativement la grille. 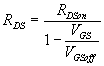 pour toute autre valeur de VGS, et en particulier RDS
tend vers l'infini si VGS = VGSoff
pour toute autre valeur de VGS, et en particulier RDS
tend vers l'infini si VGS = VGSoff 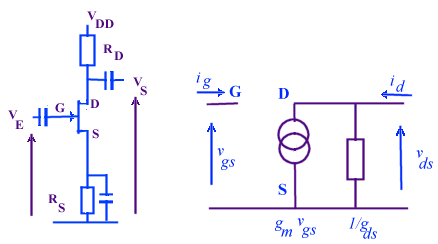
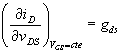 pente de la caractéristique iD = f(vDS), notons
que 1/gds varie entre 100 k
pente de la caractéristique iD = f(vDS), notons
que 1/gds varie entre 100 k et
1 M
et
1 M
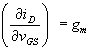 pente
de iD = f(vGS), varie typiqement entre 0.1 et 10 mA/V
pente
de iD = f(vGS), varie typiqement entre 0.1 et 10 mA/V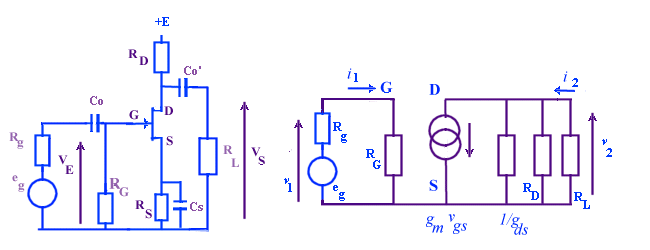
 <<
RG+Rg, de même 1/Cs
<<
RG+Rg, de même 1/Cs <<
Rs. En outre il sera nécessaire que la composante alternative
vSM (entre source et masse) soit inférieure à vgs.
Ce qui implique 1/Cs
<<
Rs. En outre il sera nécessaire que la composante alternative
vSM (entre source et masse) soit inférieure à vgs.
Ce qui implique 1/Cs << 1/gm.
<< 1/gm.
 |
 |