
Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression
22 mars 2013
 |
Copyright |
6 pages à l'impression |
version
initiale 2002 |
||
| dernière
mise à jour 22 mars 2013 |
CAPTEURS BIOMEDICAUX
sixième partie :
propriétés diélectriques des tissus biologiques (2/2)
| la
membrane cellulaire |
||||
| 3
phénomènes principaux |
||||
| quelques
modèles proposés |
||||
| une collection d'icônes pour visiter tout le site | ||||
PROPRIETES DIELECTRIQUES DES MILIEUX BIOLOGIQUES
LE MILIEU BIOLOGIQUE
Les tissus biologiques sont constitués de cellules, dont les dimensions varient entre 5 et 20 mm, baignant dans une phase aqueuse constituant le milieu extracellulaire. Les milieu intra- et extra-cellulaires sont séparés par une membrane constituée d'une double couche lipidique d'une épaisseur comprise entre 5 et 7 nm (Figure). Des macromolécules sont distribuées sur toute la surface de la cellule et certaines sont insérées au travers de celle-ci constituant ainsi des canaux d'échanges sélectifs. Le milieu aqueux intracellulaire, ou cytoplasme, renferme tous les organites assurant les fonctions vitales de la cellule.
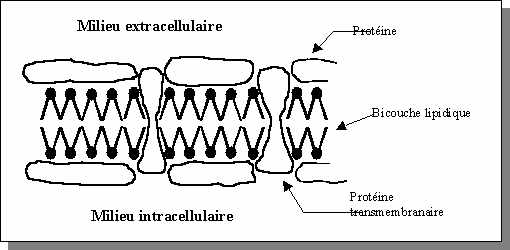
Figure:
La membrane cellulaire
La membrane
cellulaire se comporte comme un diélectrique de permittivité relative proche
de celle des lipides (approximativement 3 [RIG 96]) formant une couche isolante
séparant deux milieux conducteurs. On reconnaît la structure d'une capacité
dont la valeur peut être estimée en appliquant la formule du condensateur plan
: ![]() où e est l'épaisseur
de la membrane cellulaire et
où e est l'épaisseur
de la membrane cellulaire et  m sa permittivité
relative. Il s'agit là d'une valeur très élevée due à l'extrême finesse de la
membrane.
m sa permittivité
relative. Il s'agit là d'une valeur très élevée due à l'extrême finesse de la
membrane.
RELAXATIONS DIELECTRIQUES DANS LES TISSUS BIOLOGIQUES
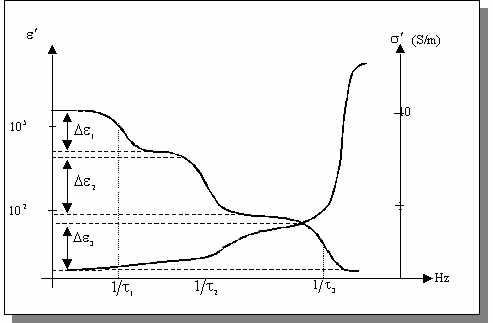
L'observation du comportement diélectrique des tissus biologiques par le tracé de l'évolution des parties réelles de la permittivité et de la conductivité en fonction de la fréquence met en évidence trois phénomènes de relaxation principaux. Ces relaxations, nommées a,b et g sont plus souvent désignées par le terme de dispersion car l'absorption diélectrique résultante est observable sur une large plage de fréquences .
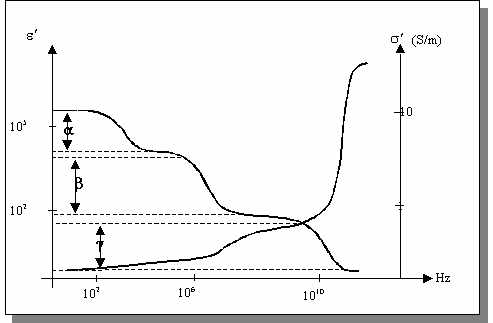
Figure
: Principaux phénomènes de relaxation observés dans les tissus biologiques.
L'origine de ces relaxations est précisée ci-dessous:
 : Sous l'effet
d'un champ électrique, un phénomène de diffusion ionique intervient à la
surface de la membrane cellulaire entraînant l'apparition d'un dipôle à
l'échelle de la cellule. Cette dispersion intervient dans la gamme des basses
fréquences, entre quelques hertz et quelques kilohertz et se traduit par
une très forte baisse de la permittivité. La conductivité ne varie pas de
façon significative. A ces fréquences, l'effet capacitif des membranes interdit
le passage du courant dans le milieu intracellulaire. La conductivité observée
est donc représentative du milieu extracellulaire.
: Sous l'effet
d'un champ électrique, un phénomène de diffusion ionique intervient à la
surface de la membrane cellulaire entraînant l'apparition d'un dipôle à
l'échelle de la cellule. Cette dispersion intervient dans la gamme des basses
fréquences, entre quelques hertz et quelques kilohertz et se traduit par
une très forte baisse de la permittivité. La conductivité ne varie pas de
façon significative. A ces fréquences, l'effet capacitif des membranes interdit
le passage du courant dans le milieu intracellulaire. La conductivité observée
est donc représentative du milieu extracellulaire.  : Intervenant
dans la gamme 500 kHz - 20 MHz, cette dispersion est principalement due
à la relaxation interfaciale associée à l'effet capacitif des membranes
cellulaires. Lorsque la fréquence augmente, la réactance capacitive de la
membrane décroît ce qui autorise la circulation d'un courant dans le milieu
intracellulaire. Il en résulte donc une augmentation de la conductivité
apparente du milieu et cette dernière devient représentative du milieu intracellulaire
en plus du milieu extracellulaire. Par ailleurs, la polarisation membranaire
n'a plus le temps de s'établir totalement ce qui se traduit par une réduction
de la permittivité apparente. La relaxation dipolaire est bien modélisée
par la théorie des mélanges de Maxwell-Wagner. En particulier, cette théorie
prévoit que même si les propriétés diélectriques des constituants du mélange
sont indépendantes de la fréquence, les propriétés du mélange sont dépendantes
de celle-ci. Enfin, dans la partie haute de cette dispersion, la réorientation
dipolaire des structures à l'échelle des organites cellulaires et des protéines
entraîne également des phénomènes de relaxation.
: Intervenant
dans la gamme 500 kHz - 20 MHz, cette dispersion est principalement due
à la relaxation interfaciale associée à l'effet capacitif des membranes
cellulaires. Lorsque la fréquence augmente, la réactance capacitive de la
membrane décroît ce qui autorise la circulation d'un courant dans le milieu
intracellulaire. Il en résulte donc une augmentation de la conductivité
apparente du milieu et cette dernière devient représentative du milieu intracellulaire
en plus du milieu extracellulaire. Par ailleurs, la polarisation membranaire
n'a plus le temps de s'établir totalement ce qui se traduit par une réduction
de la permittivité apparente. La relaxation dipolaire est bien modélisée
par la théorie des mélanges de Maxwell-Wagner. En particulier, cette théorie
prévoit que même si les propriétés diélectriques des constituants du mélange
sont indépendantes de la fréquence, les propriétés du mélange sont dépendantes
de celle-ci. Enfin, dans la partie haute de cette dispersion, la réorientation
dipolaire des structures à l'échelle des organites cellulaires et des protéines
entraîne également des phénomènes de relaxation.  : Cette dispersion est associée à
l'orientation dipolaire des molécules d'eau libre et n'intervient qu'aux
très hautes fréquences, soit aux environ de 17 GHz. A ces fréquences, les
membranes sont électriquement transparentes et le milieu est perçu comme
un électrolyte.
: Cette dispersion est associée à
l'orientation dipolaire des molécules d'eau libre et n'intervient qu'aux
très hautes fréquences, soit aux environ de 17 GHz. A ces fréquences, les
membranes sont électriquement transparentes et le milieu est perçu comme
un électrolyte. MODELISATION DES PROPRIETES ELECTRIQUES TISSULAIRES
Afin de rendre compte du comportement diélectrique des tissus biologiques, plusieurs modèles ont été proposés et découlent des théories de Maxwell [MAX 81], Wagner [WAG 14], Debye [DEB 29], Cole & Cole [COL 41] et Fricke [FRI 32]. Ces différents auteurs ont mis en place au cours de la première moitié du 20ème siècle des approches encore utilisées à ce jour. Ces principaux modèles sont décrits succinctement dans ce paragraphe.
Le modèle de Fricke
Ce modèle assimile les tissus biologiques à une suspension cellulaire dans un milieu dilué et est fondé sur un circuit électrique composé d'une capacité Cm associée en série avec une résistance Ri traduisant la présence du milieu intracellulaire. Le milieu extracellulaire est modélisé par une résistance Re
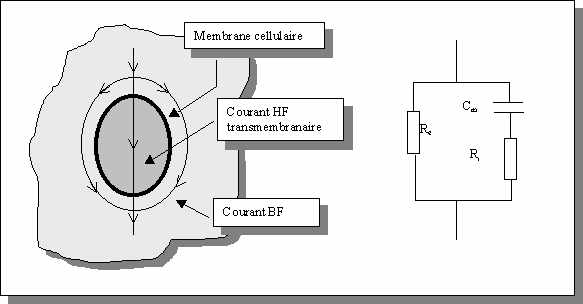
. Figure
: Modèle de Fricke
Le modèle de Debye
Ce modèle constitue la base des modèles utilisés actuellement. Il assimile la relaxation dipolaire à un système mécanique du premier ordre où les forces s'opposant à la réorientation des dipôles sont purement visqueuses, c'est à dire qu'il n'y a pas de force élastique de rappel.
La variation
de permittivité du matériau entre une valeur maximale  s
mesurée en statique et une valeur minimale
s
mesurée en statique et une valeur minimale  idéalement
observée à une fréquence infinie est décrite par l'équation suivante :
idéalement
observée à une fréquence infinie est décrite par l'équation suivante : ![]()
où  caractérise la constante de temps du phénomène de relaxation considéré.
caractérise la constante de temps du phénomène de relaxation considéré.
Cette équation peut être séparée en ses parties réelles et imaginaires pouvant être tracées en fonction de la fréquence ou l'une par rapport à l'autre dans le plan complexe (diagramme d'Argand) .
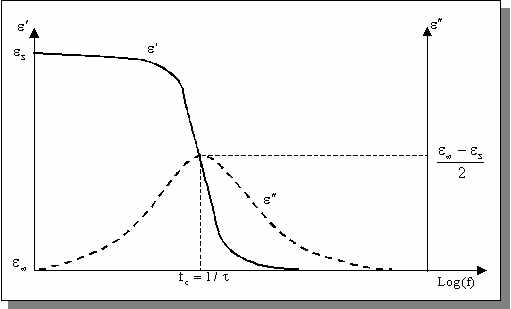
Figure:
Parties réelle et imaginaire de la permittivité [d'après RIG 96]
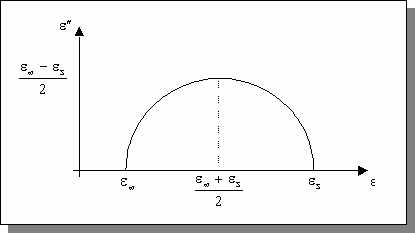
Figure
: Partie imaginaire en fonction de la partie réelle de la permittivité (diagramme
d'Argand) (d'après [RIG 96])
![]()
Par ailleurs, ce modèle ne peut distinguer la contribution de plusieurs phénomènes de relaxation distincts caractérisés par des constantes de temps différentes. Afin d'introduire plusieurs constantes de temps, l'équation précédente devient :
![]()
L'axe des
fréquences est divisé en intervalles centrés sur leur fréquence caractéristique
1/ respective et
respective et 
 donne la différence entre la permittivité mesurée au début de l'intervalle et
la permittivité mesurée à la fin de l'intervalle de fréquence
donne la différence entre la permittivité mesurée au début de l'intervalle et
la permittivité mesurée à la fin de l'intervalle de fréquence
. Figure
: Paramètres de l'équation de Debye modifiée (d'après [RIG 96])
L'équation 3 peut être représentée sous la forme d'un réseau électrique donné par la figure suivante.

Figure
: Réseau équivalent à l'équation de Debye
Le paramètre k est un facteur géométrique (cm-1) (d'après [RIG 96])
Le modèle de Cole-Cole
Le modèle
de Debye
modifié ne permet d'introduire qu'une suite de valeurs discrètes des constantes
de temps  . Cependant, le comportement
de milieux aussi hétérogènes que les tissus biologiques est plus complexe. Le
modèle de Cole-Cole (d'après Cole et Cole [COL 41]) introduit la notion de dispersion,
au sens où les constantes de temps sont réparties suivant une distribution gaussienne
autour d'une constante de temps moyenne
. Cependant, le comportement
de milieux aussi hétérogènes que les tissus biologiques est plus complexe. Le
modèle de Cole-Cole (d'après Cole et Cole [COL 41]) introduit la notion de dispersion,
au sens où les constantes de temps sont réparties suivant une distribution gaussienne
autour d'une constante de temps moyenne  c.
Lorsque la conductivité statique est prise en compte, l'équation de Cole-Cole
est donnée par :
c.
Lorsque la conductivité statique est prise en compte, l'équation de Cole-Cole
est donnée par :
![]()
Le paramètre
 permet d'ajuster la largeur
de la dispersion. Lorsque
permet d'ajuster la largeur
de la dispersion. Lorsque  = 0, il n'y a pas de dispersion et on retrouve l'équation de Debye. Le tracé
de la partie imaginaire de cette équation en fonction de sa partie réelle dans
le plan complexe montre que cette nouvelle formulation permet de rendre compte
de faits expérimentaux non retrouvés avec le modèle de Debye. En particulier,
la hauteur maximale du cercle (maximum de
= 0, il n'y a pas de dispersion et on retrouve l'équation de Debye. Le tracé
de la partie imaginaire de cette équation en fonction de sa partie réelle dans
le plan complexe montre que cette nouvelle formulation permet de rendre compte
de faits expérimentaux non retrouvés avec le modèle de Debye. En particulier,
la hauteur maximale du cercle (maximum de  "
) observée expérimentalement est inférieur à la valeur
"
) observée expérimentalement est inférieur à la valeur ![]() prévue par le modèle de Debye. Le modèle de Cole-Cole permet de rendre compte
de ce phénomène.
prévue par le modèle de Debye. Le modèle de Cole-Cole permet de rendre compte
de ce phénomène.
Comme l'équation de Debye, l'équation de Cole-Cole admet un réseau électrique équivalent donné par la figure ci-dessous. Afin de rendre compte de la distribution des constantes de temps, une impédance à phase constante ZCPE est introduite. D'après McAdams et Jossinet [MCA 95], ce réseau n'a pas de réalité physique et ne prouve pas l'existence physique de la distribution des temps de relaxation. Il doit donc être considéré comme un moyen empirique de décrire les résultats expérimentaux [RIG 96].
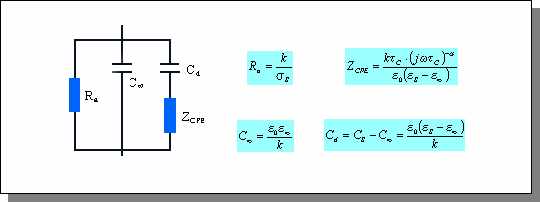
Figure
: Réseau équivalent à l'équation de Cole-Cole
Le paramètre k est un facteur géométrique (cm-1) (d'après [RIG 96])
Evidemment,
le modèle de Cole-Cole peut être amélioré en introduisant une série de temps
de relaxation 1,
1,  2,
2,  3
... à l'image du modèle de Debye amélioré.
3
... à l'image du modèle de Debye amélioré.
{CHA 00] : J.F. CHATEAUX, "Conception et réalisation d'une cellule de caractérisation des tissus biologiques par spectroscopie de bioimpédance dans la gamme fréquentielle (100 Hz-1 MHz), application aux tissus osseux-prise en compte de l'anisotropie", Thèse de Doctorat, Université Henri Poincaré, Nancy I, 15 novembre 2000
[COL 41] : K. S. COLE, R. H. COLE, " Dispersion and absorption in dielectrics. I. Alternating current characteristics '', Journal of Chemical Physics, Vol. 9, pp. 341-351,1941.
[DEB 29] : P. DEBYE, " Polar molecules '', Edition New York : The chemical catalog, 1929
[FRI 32] : H. FRICKE, " The theory of electrolytic polarization '', Phil. Mag., pp. 310-318, 1932.
[INA 99] : U.S. INAN, A.S. INAN, "Engineering electromagnetics", Addison-Wesley, 1999.
[MAX 81] : J. C. MAXWELL, " A treatise on electricity and magnetism '', 2ème édition, Edition Oxford : Clarendon Press, 1881.
[MCA 95] : E. T. McADAMS, J. JOSSINET, " Modélisation du comportant à 'angle de phase constant' des tissus biologiques : pièges possibles '', Innov. Tech. Biol. Med., Vol. 16 (6), pp. 661-670, 1995.
[PER 97] : J-P. PEREZ, R. CARLES, R. FLECKINGER, "Electromagnétisme : Fondements et applications", 3ème Ed., Masson, 1997.
[RIG 96] : B. RIGAUD, J.-P. MORUCCI, N. CHAUVEAU, " Bioelectrical impedance techniques in medicine. Part I : Bioimpedance measurement. Second section : Impedance spectrometry '', Critical Reviews in Biomedical Engineering, Vol. 24 (4-6), p. 257-351, 1996.
[WAG 14] : K. W. WAGNER, " Explanation of the dielectric fatigue phenomenon on the basis of Maxwell's concept '', Arkiv für Electrotechnik - Edition Shering H. Berlin : Springer-Verlag, 1914.