Copyright © 2000-2015 LHERBAUDIERE	5 pages à l'impression			version initiale 2002
	INFORMATION				dernière mise à jour 22 mars 2013

CAPTEURS BIOMEDICAUX

cinquième partie : les tissus biologiques (1/2) notions fondamentales

conducteur			le milieu conducteur
milieu diélectrique			polarisation, courant de déplacement
mileu à pertes			.
phénomènes de relaxation			les constantes de temps
conductivité complexe			.
impédance			.
				une collection d'icônes pour visiter tout le site

Nous empruntons à J.F. Châteaux [CHA 00] l'essentiel de ce chapitre.

Avant d'aborder la mesure des propriétés électriques des tissus biologiques, il est utile de rappeler quelques notions fondamentales relatives au propriétés électriques de la matière. En particulier, les notions de courant de déplacement, de permittivité complexe, de relaxation et de dispersion sont exposées le plus simplement possible afin de conférer à l'exposé un caractère didactique. Dans un premier temps, ces notions sont présentées dans le cadre des matériaux diélectriques en général. Elles sont alors reprises en vue d'une description plus spécifiquement orientée vers le comportement diélectrique des tissus biologiques.

NOTIONS FONDAMENTALES

MILIEU CONDUCTEUR, COURANT DE CONDUCTION

Dans les milieux contenant des charges libres (électrons dans les métaux, ions dans les électrolytes) l'application d'un champ électrique produit une force sur chacune des charges q suivant la relation :

Sous l'action de cette force, les charges libres se déplacent suivant la direction du champ électrique. Ce mouvement se traduit à l'échelle macroscopique par l'apparition d'un courant dont la densité est liée au champ électrique par la relation :

Cette relation, la loi d'Ohm, définit la conductivité électrique exprimée en Siemens par mètre (S.m-1) comme étant le facteur de proportionnalité entre densité de courant et champ électrique. Le courant résultant du déplacement des charges libres est appelé courant de conduction. Les milieux ne comportant pas de charges libres ne peuvent être le siège d'aucun courant de conduction et à ce titre sont qualifiés d'isolant.

---

MILIEU DIELECTRIQUE, POLARISATION, COURANT DE DEPLACEMENT

Les milieux isolants, (ou diélectriques en raison des propriétés énoncées dans les lignes qui suivent) ne peuvent par définition être le siège d'un courant de conduction. Cependant, comme toute matière, ces milieux sont formés de charges positives et négatives liées à l'intérieur d'atomes et de molécules. Pour certaines de ces molécules (comme l'eau), le centre de gravité des charges positives ne coïncide pas avec celui des charges négatives. Il en résulte l'apparition d'un dipôle électrique qualifié de permanent car intrinsèque au milieu considéré.

Des dipôles induits sont par ailleurs créés au sein d'un diélectrique par l'application d'un champ électrique dont l'action développe une force, identique à celle produisant un courant dans les conducteurs, entraînant une migration des charges liées positives et négatives présents dans les molécules.

Un dipôle, qu'il soit permanent ou induit, est caractérisé par son moment dipolaire dont l'amplitude est le produit de la charge par la distance séparant ses pôles. Par nature, les dipôles induits sont alignés sur le champ les créant. Si un tel champ est appliqué à un milieu comportant des dipôles permanents, ces derniers s'alignent suivant les lignes de champ en raison de leur moment dipolaire (création d'un couple de forces). Cette orientation des dipôles suivant une direction privilégiée entraîne la polarisation du milieu soumis au champ électrique . La densité volumique de moments dipolaires, observée en tout point du milieu, définit le champ de polarisation . Le déplacement électrique , effet du champ électrique sur la matière, est alors défini par :

où est la permittivité diélectrique du vide.

Si le milieu est linéaire, la polarisation est proportionnelle au champ électrique et on a : où est la permittivité du matériau. Dans le vide, où la polarisation est nulle, le déplacement électrique vaut donc :

On définit en pratique la permittivité relative comme étant le rapport de la permittivité du matériau à celle du vide : Ce terme est également appelé constante diélectrique du matériau.

Si le champ électrique varie dans le temps, sinusoïdalement par exemple, un mouvement oscillatoire des dipôles apparaît en raison de leur tendance à s'aligner sur le champ électrique. Bien que ces oscillations se fassent sur place et qu'il n'y a donc pas de réelle migration des dipôles, ce mouvement local est assimilable à un courant alternatif appelé courant de déplacement. Ce nom peut paraître un peu paradoxal mais a justement été choisi par Maxwell, qui a introduit cette notion, pour indiquer que ce courant résulte du déplacement alternatif de charges liées [INA 99].

De façon plus pratique, le courant de conduction est celui qui circule dans une résistance pure alors que le courant de déplacement est celui qui circule au travers d'une capacité pure.

---

MILIEU DIELECTRIQUE A PERTES

Au paragraphe précédent nous avons rappelé que les dipôles, permanents ou induits, présents dans les diélectriques s'alignent suivant la direction du champ électrique . Cependant, cette rotation des dipôles doit s'opposer à des forces de frottement, à des forces de rappel ainsi qu'à l'agitation des atomes et molécules due à la température ambiante. L'existence de ces forces s'opposant à l'orientation des dipôles a une double conséquence, en particulier lorsque le champ électrique appliqué est variable et de haute fréquence :

• Le travail développé pour contrecarrer les forces de friction consomme de l'énergie prélevée au champ électrique. Cette énergie se dissipe dans le matériau sous forme de chaleur. C'est ainsi que fonctionnent les fours à micro-ondes. Un diélectrique absorbant de l'énergie par ce mécanisme est qualifié de diélectrique à pertes.

• L'orientation des dipôles se fait avec un certain retard. Ce retard est négligeable lorsque le champ électrique varie lentement et les champs et sont alors en phase. Cependant, lorsque la fréquence augmente, le retard devient significatif et les champs et ne sont plus en phase. Afin de traduire ce déphasage, la permittivité définie plus haut est remplacée par une grandeur complexe dont la partie imaginaire traduit les pertes énergétiques et on note :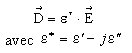

---

PHENOMENES DE RELAXATION

En réalité, de nombreux mécanismes de polarisation coexistent et on peut distinguer ainsi :

• La polarisation d'orientation résultant de l'orientation des molécules dipolaires rigides [PER 97].

• La polarisation ionique, due au déplacement des ions positifs par rapport aux ions négatifs dans les molécules à liaison ionique.

• La polarisation électronique due à la déformation du nuage électronique des atomes.

Une augmentation de la partie imaginaire, traduisant des pertes plus importantes.
Une réduction de la partie réelle, traduisant une réduction de la capacité du matériau à se polariser. Ce dernier point est tout à fait compréhensible car un des mécanismes contribuant à la polarisation globale n'agit plus celui-ci étant incapable de suivre les variations du champ électrique.

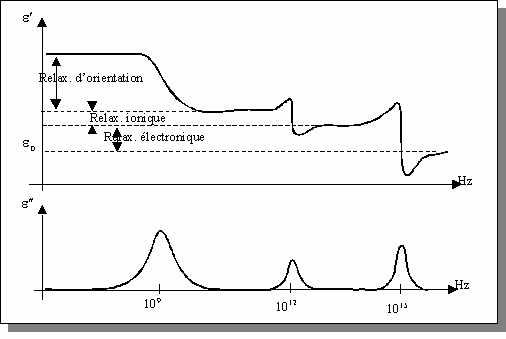
Figure Phénomènes de relaxation et mécanismes de polarisation associés(d'après [PER 97])

La permittivité complexe est donc une grandeur dépendante de la fréquence qu'on peut donc écrire ^*().

CONDUCTIVITE COMPLEXE

Jusqu'à présent, les milieux diélectriques considérés ont été supposés parfaitement isolants, les seules pertes énergétiques les affectant étant dues aux phénomènes de relaxation. De nombreux matériaux cependant, dont les tissus biologiques, sont à la fois diélectriques et conducteurs : leur conductivité n'est pas nulle.

L'application d'un champ électrique à un tel milieu engendre donc un courant de conduction ainsi qu'un courant de déplacement dans le cas d'un champ variable. Aux pertes diélectriques évoquées précédemment s'ajoutent donc des pertes ohmiques par effet Joule.

Dans le cadre d'un champ électrique harmonique , la densité de courant résultante dans le milieu s'exprime par : avec le courant de conduction et le courant de déplacement. En introduisant la notation _s pour la conductivité statique (qui n'est rien d'autre que la conductivité normale d'un conducteur mesurée à n'importe quelle fréquence), on a alors :

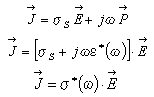
*() étant la conductivité complexe. Le lien entre conductivité et permittivité complexe peut alors être explicité comme suit :

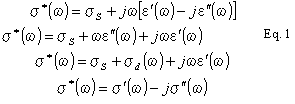
Le terme _d()est appelé conductivité dynamique et permet de regrouper en un terme unique '() les pertes ohmiques liées à _s et les pertes diélectriques dues à "() . Ce regroupement est possible car l'équation (1) montre que les pertes diélectriques sont en phase avec les pertes ohmiques et se comportent donc comme si un nouveau courant de conduction venait se superposer au courant ohmique "normal" lié à s_s.

Ainsi, les parties réelles et imaginaires de la conductivité complexe s'écrivent :

traduisant l'ensemble des pertes dans le milieu (ohmique + diélectrique)
traduisant la polarisation du matériau, c'est à dire son aptitude à stocker de l'énergie sous forme d'un champ électrique.

La conductivité complexe et la permittivité complexe sont donc liées par la relation :

ce qui permet d'écrire encore :

Cette dernière relation est plus particulièrement utilisée pour la description des diélectriques à faibles pertes alors que la conductivité complexe est plutôt utilisée lorsque le milieu est bon conducteur.

---

IMPEDANCE

La détermination de la conductivité statique _s, de la conductivité dynamique _d() et de la permittivité '() suffit à la complète caractérisation diélectrique des matériaux. Cependant, ces grandeurs ne sont pas mesurables directement et sont généralement déduites d'une mesure d'impédance. L'impédance Z* traduit la relation entre la tension aux bornes d'un circuit et le courant le traversant suivant la relation bien connue (loi d'Ohm à l'échelle macroscopique) :

Toutes les grandeurs de cette relation sont complexes, ce qui traduit un éventuel déphasage entre la tension et le courant. L'impédance est liée à la conductivité et à la permittivité suivant une relation dépendant de la géométrie du champ électrique baignant le milieu. Ainsi, dans le cas d'un milieu cylindrique relié à des électrodes de même diamètre (Figure) et en négligeant tout effet de bord, l'impédance (en ohms ) est donnée par l'équation :

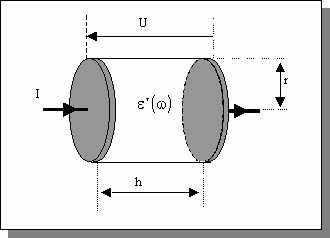
Figure: Impédance dans le cas d'une géométrie cylindrique