cliquez sur le mot avertissement
ou information ci-dessus
pour connaitre une info essentielle avant de lire ce module et n'hésitez
pas à cliquer en bas de page sur l'icone sommaire
du site ça vous ouvrira d'autres perspectives
Eléments de Magnétisme
Dans ce chapitre
nous allons tenter une gageure, celle d'expliquer
pourquoi certains matériaux ont des propriétés magnétiques
particulières. En effet après avoir visionné des dizaines
d'ouvrages de physique, qu'ils soient écrits par un prix Nobel ou un
simple enseignant de lycée, nous restons sur notre faim, aucun n'a été
capable de nous donner une explication crédible et compréhensible
du magnétisme. Alors nous allons tenter une explication.
l'atome isolé
Dans un autre
chapitre au début de ce module de physique et d'électronique nous
avons donné quelques éléments concernant la structure de
l'atome, nous allons y revenir ici. Considérons donc un atome isolé,
ce qui est donc une situation purement théorique
puisqu'il nous est impossible d'observer un atome isolé, le seul fait
de nous approcher suffisamment près de lui pour l'observer entrainant
dde fait qu'il ne soit plus isolé et donc qu'il soit perturbé
par notre approche. Une image classique quoique très approximative, comme
on va le voir, consiste à dire qu'un tel atome a une structure (ou une
configuration) s'apparentant au système solaire. Cette image destinée
à impressionner le béotien est malheureusement inexacte sur bien
des points. Dans un atome on distingue en effet des électrons que cette
image assimile à nos planètes et un noyau qui serait donc comme
le soleil.
Les différences
essentielles proviennent de deux éléments
: d'une part, tous les électrons ont des propriétés dimensionnelles
semblables et sont chargés électriquement d'une même
charge élémentaire négative ce qui les différentie
sensiblement des planètes qui sont non chargées et toutes de taille
différente, d'autre part, le noyau de l'atome est constitué de
nombreuses particules en mouvement, mais il est d'une grande densité
puisque son volume est sensiblement équivalent à celui
d'un électron, alors que notre soleil a sensiblement un rayon 100 fois
supérieur à celui de la terre (soit un volume 1300000 fois plus
important). La comparaison est donc très simpliste.
Dans le cas
d'un atome isolé il y a cependant un élément de
comparaison que l'on peut admettre comme équivalent c'est la
stabilité des trajectoires des mobiles autour du noyau central.
En effet dans notre système solaire, depuis Kepler,
on sait déterminer avec une grande précision les mouvements des
planètes, à tel point qu'on peut à une date précise
lancer vers l'espace une fusée dont on sait que sa trajectoire l'amènera
quelques années plus tard (à une date parfaitement connue à
l'avance) à s'écraser sur Vénus. Dans l'atome isolé
il en est de même, chaque électron possède un état
énergétique défini par quatre nombre
quantiques dont il résulte une trajectoire parfaitement définie
(en forme d'ellipsoïde de révolution pour les plus énergétiques
et de sphère pour les plus proches du noyau) mais que nous ne pouvons
évidemment suivre. En fait, compte tenu de ce que nous savons des lois
de la mécanique et de l'électromagnétisme, il est clair
que les trajectoires relatives de chacun des électrons de notre atome
isolé ne sont pas indépendantes les unes des autres. En d'autres
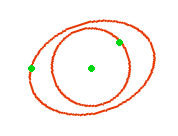
termes si pour une raison ou une autre nous parvenions à "décaler"
un électron sur sa trajectoire sans cependant changer en quoi que ce
soit son niveau énergétique il est évident que l'ensemble
des trajectoires des autres électrons subiraient une perturbation sans
changement de niveau d'énergie. Un électron se déplaçant
sur une sphère ne serait probablement pas perturbé, tandis qu'un
électron sur un ellipsoide de révolution le serait. Quelle forme
pourrait prendre cette perturbation? En admettant que le niveau d'énergie
reste invariant on peut imaginer que c'est l'ellipsoide de révolution
qui pourrait tout simplement changer l'orientation de son grand axe, donc légèrement
tourner autour du noyau, celui-ci restant évidemment à l'un des
foyers de l'ellipsoide.
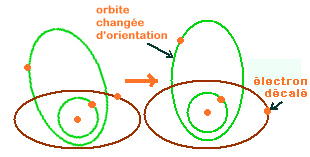
Que se passerait-il
ensuite si l'on venait à supprimer la cause de la perturbation? Il est
tout aussi intuitif que cela entrainerait un nouvel équilibre
donc une nouvelle configuration respective des ellipsoides de révolution,
mais la probabilité pour qu'on revienne à l'état initial
est évidemment très voisine de zéro.
L'expérimentation
ci-dessus correspond sensiblement à ce qui se passerait pour un atome
isolé placé dans un champ magnétique. Il s'agit donc d'un
effet minime caractéristique des matériaux dits paramagnétiques.
cas
d'un atome ferromagnétique
Dans cet exemple
académique nous avons supposé avoir affaire à un atome
quelconque, c'est à dire en fait un atome non particulier. Mais, ainsi
que nous le montre la classification périodique des éléments
il y a des éléments sensiblement différents des autres,
c'est le cas des matériaux qui vont nous intéresser ici que l'on
qualifie de ferromagnétiques : le fer, le nickel et le cobalt. Est-ce
que si l'on reproduit avec un atome de l'un de ces métaux l'expérience
précédente on va obtenir le même résultat? La réponse
n'est pas forcément oui, car elle va dépendre de quel électron
je vais perturber.
En effet,
si l'on regarde les niveaux énergétiques définis par la
théorie quantique pour chaque couche électronique et qu'on les
place par valeur croissante sur une échelle on va découvrir qu'il
existe des niveaux énergétiques théoriques de valeur équivalente
pour deux couches successives. Dans un atome réel ces niveaux équivalents
peuvent être occupés ou non. Dans les matériaux comme le
nickel l'occupation des niveaux pour un atome non excité, et compte tenu
du nombre d'électrons de ce matériau, est particulière
car le niveau _ est normalement inoccupé tandis que le niveau _ l'est
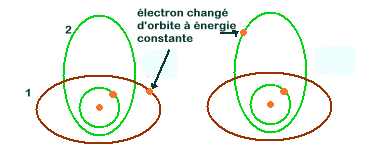
ainsi que les niveaux supérieurs _. Essayons de représenter graphiquement
la projection sur un plan des ellipsoides correspondant à ces deux niveaux
équivalents.
Quoique ils
correspondent à des énergies équivalentes, ceux-ci ne sont
pas confondus car ils correspondent à des valeurs différentes
du premier nombre quantique et à des excentricités différentes
des ellipsoides. La figure montre que ces deux volumes sont sécants.
Cela veut dire quoi? Cela veut dire que si l'électron qui tourne sur
1 est soumis à une miniperturbation susceptible de "changer sa direction"
il va pouvoir passer sur une trajectoire 2. C'est ce qui va se produire s'il
est soumis à un champ électromagnétique et comme il n'y
a pas de changement énergétique lorsque la cause de la perturbation
cesse il n'y a aucune raison que notre électron revienne sur son ancienne
trajectoire.
Qu'a-t-on
omis dans ce raisonnement? une chose essentielle, c'est que l'ellipsoide 2 était
virtuel puisque inoccupé, donc mon schéma a priori était
tendancieux : une infinité d'autres ellipsoides d'axe différent
pouvaient tout aussi bien convenir a priori (puisque représentatifs de
la même énergie), mais un seul a été effectivement
utilisé, et pas n'importe lequel, mais celui qui était le mieux
orienté par rapport au champ appliqué, et il est clair
qu'il n'y en a qu'un qui corresponde à cet optimum.
cas
d'un solide ferromagnétique
Si maintenant
on refait la même expérience, non plus avec un atome de Ni ou de
fer mais avec un morceau de fer pur (ce qu'on appelle communément du
fer doux) contenant n atomes. Pour chaque atome le même processus va se
produire, tous les électrons 2 vont circuler sur des ellipsoides semblables
et de même orientation en présence du champ. Mais dès qu'on
va supprimer le champ que va-t-il se passer? Les atomes ne sont plus isolés,
ils sont très proches puisqu'il s'agit d'un solide en conséquence
chaque perturbation survenant sur un atome va influencer non seulement les électrons
de cet atome mais aussi ceux de ses plus proches voisins et l'on peut donc en
conclure que la présence du champ a donc induit sur chaque atome du solide
une pertubation bien plus importante qu'il n'avait produit sur l'atome isolé,
mais dès que le champ cesse le nouvel équilibre est complètement
perturbé et on va revenir à un nouvel état d'équilibre
qui sans être exactement celui de départ va s'en rapprocher fortement
et les électrons 2 qui étaient sur des trajectoires orientées
parallèlement vont souvent revenir sur des trajectoires 1 qui auront
une orientation statistiquement quelconque.
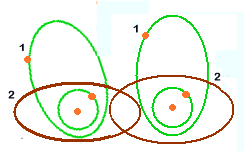modèle
simplifié montrant l'additivité (électrons en 2) et l'interpénétration
des orbites pour des atomes au sein d'un solide
(il faut évidemment imaginer
ce modèle en trois dimensions avec n atomes)
Donc en présence du champ on va avoir une organisation des électrons
2 avec donc une certaine additivité de leurs moments magnétiques
d'où il résulte globalement le phénomène qu'on appelle
aimantation, mais cette aimantation va cesser dès que le champ qui la
génère disparait car chaque électron concerné va
interragir électromagnétiquement avec ceux des atomes voisins
et, en raison de cet équivalence de niveaux d'énergie non occupés,
des transferts inverses d'une bande d'énergie à l'autre vont se
produire et très vite la désorganisation va s'installer.
Pourquoi cependant
certains matériaux une fois magnétisés conservent
leur aimantation? La réponse est simple, il s'agit non de métaux
purs mais d'alliages ou de combinaisons faisant intervenir non seulement des
atomes de Fer Ni ou Co mais aussi d'autres atomes qui eux ne sont pas sensibles
au phénomène d'aimantation car ils ne possèdent pas cette
structure électronique particulière aux ferromagnétiques,
c'est par exemple le cas de la magnétite Fe3O4. Par contre ces atomes
ont comme conséquence de maintenir les atomes ferromagnétiques
éloignés les uns des autres d'au
moins une distance atomique, distance suffisante pour que les interactions électromagnétiques
responsables du retour à la désorganisation soient inexistantes.
En conséquence un tel matériau une fois magnétisé
va rester aimanté avec l'apparition d'un pôle N et d'un pôle
S aux extrémités opposées compte tenu de la direction du
champ créateur.
