généralités
(rappels)
Le champ magnétique H (en At/m) dans un tore s'exprime par 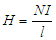 où N représente le nombre de tours, l la longueur du tour et I
l'intensité du courant. L'induction magnétique B = µH dans
un milieu ferromagnétique avec µ = µ0µr.
Si le milieu n'est pas saturé µr est une constante,
sinon µr dépend de H.
où N représente le nombre de tours, l la longueur du tour et I
l'intensité du courant. L'induction magnétique B = µH dans
un milieu ferromagnétique avec µ = µ0µr.
Si le milieu n'est pas saturé µr est une constante,
sinon µr dépend de H.
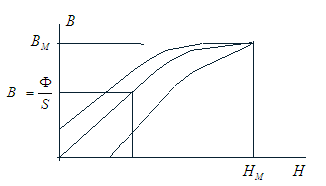 hystérésis et saturation
hystérésis et saturation
Dans le cas d'un circuit magnétique réel il faut tenir compte
du coefficient d'Hopkinson 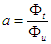 ,
ainsi dans un électro-aimant
,
ainsi dans un électro-aimant 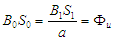 d'où un rapport S1/S0 élevé.
d'où un rapport S1/S0 élevé.
Si le flux est alternatif
 = Li avec L constant et proportionnel à
N2 (pour un non ferromagnétique) et variable avec µr
(pour un ferromagnétique)
= Li avec L constant et proportionnel à
N2 (pour un non ferromagnétique) et variable avec µr
(pour un ferromagnétique)
la fem d'induction étant 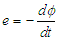
Dans un circuit magnétique traversé par un flux magnétique
on a donc des pertes fer
- hystérésis : formule empirique
de Steinmetz
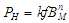 les pertes s'expriment en W/kg, k est un coefficient empirique de l'ordre
de 0.02 , f est la fréquence en Hz tandis que 1.6 < n < 2
les pertes s'expriment en W/kg, k est un coefficient empirique de l'ordre
de 0.02 , f est la fréquence en Hz tandis que 1.6 < n < 2
L'hystérésis semblerait du à l'absorption d'énergie
(équivalente à des frottements) résultant du changement
d'orientation des dipôles élémentaires avec le champ.
- Courants de Foucault : il s'agit de courants induits dans le fer
par suite des variations de flux, on va les minimiser en augmentant la résistance
des tôles constitutives du transformateur : d'une part, en utilisant
du fer au silicium et, d'autre part, en feuilletant le circuit dans la direction
du flux ce qui a pour effet d'augmenter la longueur des circuits parcourus
par les courants de Foucault. Ces pertes sont du type
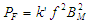
En conséquence on va avoir entre fem et flux les relations suivantes
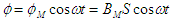 flux à
travers une spire de section S
flux à
travers une spire de section S
fem dans la spire 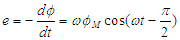 soit une valeur efficace
soit une valeur efficace 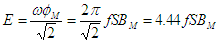
théorie
Soit un solénoide dans lequel on a mis un noyau de fer doux en forme
d'anneau par exemple. Lorsque le courant circcule il induit un champ magnétique
dont les lignes d'induction dont dans l'anneau pour la plupart (elles n'en sortent
qu'à une extrémité pour rentrer dans l'autre).
Sous cette forme, il y a une analogie évidente entre les lignes d'induction
du circuit magnétique et les lignes de courant d'un circuit électrique.
Appliquons le théorème d'Ampère au tube d'induction
ainsi créé (de section S faible de telle sorte que B y soit constante).
Si le solénoide possède n spires il vient 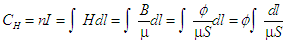 où µ est la perméabilité absolue du milieu considéré
où µ est la perméabilité absolue du milieu considéré
On peut écrire 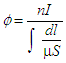 ce qu'on peut comparer à
ce qu'on peut comparer à 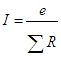 (loi d'Ohm) la quantité
(loi d'Ohm) la quantité 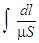 est l'analogue magnétique de la résistance électrique,
on l'appelle réluctance R tandis que nI cause du flux joue le
même rôle que la fem e (cause du courant) et s'appelle pour cela
force magnéto-motrice FMM = F d'où
F = Rf (loi d'Hopkinson).
est l'analogue magnétique de la résistance électrique,
on l'appelle réluctance R tandis que nI cause du flux joue le
même rôle que la fem e (cause du courant) et s'appelle pour cela
force magnéto-motrice FMM = F d'où
F = Rf (loi d'Hopkinson).
Problème fondamental du circuit magnétique
Etant donné un circuit magnétique comportant plusieurs tronçons
de différentes substances le problème est :
- soit une FMM étant appliquée à un circuit trouver
le flux engendré dans le circuit
- soit un flux donné devant être engendré dans un circuit
trouver la FMM nécessaire.
Ex: un circuit en 3 tronçons supposés traversés par le
même flux
F =f SR soit
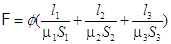 or les perméabilités
µ dépendent de B1, B2, B3 que l'on ne connait pas si l'on ne connait
pas
or les perméabilités
µ dépendent de B1, B2, B3 que l'on ne connait pas si l'on ne connait
pas  . De plus une partie du flux va se dériver
dans l'air, là où la bobine n'existe pas, de telle sorte que
. De plus une partie du flux va se dériver
dans l'air, là où la bobine n'existe pas, de telle sorte que  n'est pas constant en général dans les divers tronçons
du circuit magnétique. Le flux
n'est pas constant en général dans les divers tronçons
du circuit magnétique. Le flux  1
dans la bobine sera supérieur au flux
1
dans la bobine sera supérieur au flux  2
dans une section extérieure à la bobine, la différence
2
dans une section extérieure à la bobine, la différence
 1 -
1 -  2
=
2
=  sera le flux de fuite et le rapport
sera le flux de fuite et le rapport
 1/
1/ 2
le coefficient de fuite
2
le coefficient de fuite ou coefficient d'Hopkinson.
Les lois de
Kirchhoff s'appliquent aux circuits magnétiques : des FMM en série
s'ajoutent algébriquement, cependant que les flux en parallèle
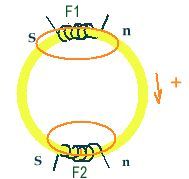
s'ajoutent. Ainsi dans la figure ci-dessous si les FMM sont opposés il
en résulte d'importantes fuites magnétiques.
On tire de
ceci les applications au transformateur.





 = Li avec L constant et proportionnel à
N2 (pour un non ferromagnétique) et variable avec µr
(pour un ferromagnétique)
= Li avec L constant et proportionnel à
N2 (pour un non ferromagnétique) et variable avec µr
(pour un ferromagnétique)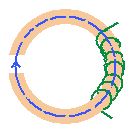
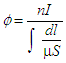 ce qu'on peut comparer à
ce qu'on peut comparer à 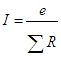 (loi d'Ohm) la quantité
(loi d'Ohm) la quantité 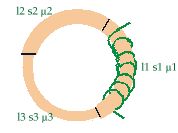
 . De plus une partie du flux va se dériver
dans l'air, là où la bobine n'existe pas, de telle sorte que
. De plus une partie du flux va se dériver
dans l'air, là où la bobine n'existe pas, de telle sorte que  n'est pas constant en général dans les divers tronçons
du circuit magnétique. Le flux
n'est pas constant en général dans les divers tronçons
du circuit magnétique. Le flux  1
dans la bobine sera supérieur au flux
1
dans la bobine sera supérieur au flux  2
dans une section extérieure à la bobine, la différence
2
dans une section extérieure à la bobine, la différence
 1 -
1 -  2
=
2
=  sera le flux de fuite et le rapport
sera le flux de fuite et le rapport
 1/
1/ 2
le coefficient de fuite ou coefficient d'Hopkinson.
2
le coefficient de fuite ou coefficient d'Hopkinson.