Copyright
© 2000-2015 LHERBAUDIERE


3 pages à l'impression		 Hit-Parade version initiale 2000
AVERTISSEMENT dernière mise à jour
18 mars 2013
cliquez sur le mot avertissement ou information ci-dessus pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives

Couplage par mutuelle inductance
Application au transformateur

généralités des rappels
équations fondamentales la base
coefficient de couplage le problème
transformateur industriel le transfo d'alimentation
circuit couplé à secondaire accordé le transformateur de liaison
primaire et secondaire accordés influence du couplage
compléments des mesures pratiques
une collection d'icônes pour visiter tout le site
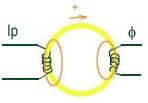
généralités
C'est le système de couplage le plus employé en radio-électricité. Il résulte d'un échange de flux magnétique entre deux bobinages isolés électriquement l'un de l'autre (primaire, secondaire)


Si le primaire est parcouru par ip = Ip sint un flux de même forme est produit par les spires de ce bobinage, flux dont une fraction coupe les spires du bobinage secondaire. Si M est le coefficient d'induction mutuelle entre les deux bobinages, il apparait aux bornes du secondaire une fem induite soit, en utilisant la notation complexe,

Si le secondaire est un circuit fermé, la fem es va engendrer un courant is lequel produit à son tour un flux dont une fraction induit dans l'enroulement primaire une fem ep telle que

équations fondamentales
Appelons E la fem du primaire, Zp et Zs les impédances du primaire et du secondaire (non couplées). On peut alors écrire (loi de Kirchhoff)


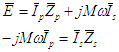
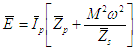
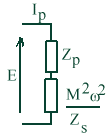On en déduit immédiatement Is = f(Ip) et en reportant dans l'expression de E on obtient

La présence du secondaire couplé au circuit primaire se traduit donc par une modification de l'impédance de celui-ci et le schéma équivalent du primaire devient :

tandis que la relation Is = f(Ip) conduit pour le secondaire au schéma ci-contre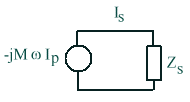
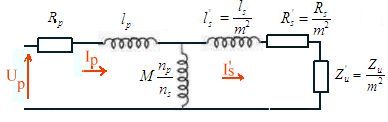
coefficient de couplage
Si np et ns sont le nombre de spires des enroulements p et s, Lp et Ls les coefficients de self inductance, on peut montrer si l'on appelle ls et lp les inductances de fuite que de même que

d'où l'on déduit facilement

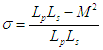Et si l'on ramène toutes les fuites au primaire en supposant ls = 0, on obtient l'inductance totale de fuite Np telle que soit ce sont les coefficients de Boucherot. On caractérise parfois le couplage par le coefficient de dispersion de Blondel ou le coefficient de couplage notons que Np = s Lp

transformateur industriel (transformateur d'alimentation)
En dehors des relations précédentes, on peut faire intervenir la présence d'un noyau de fer qui canalise les lignes d'induction. Si l'on appelle le flux utile et R la réluctance du circuit magnétique, la loi d'Hopkinson nous permet d'écrire une relation supplémentaire du type

Très souvent on néglige la réluctance et les pertes, on a alors ce qu'on appelle un transformateur idéal défini par

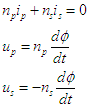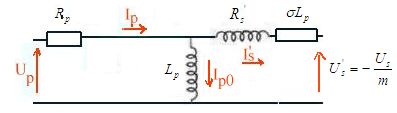
d'où on tire en posant m = ns/np 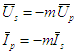et le schéma équivalent à un transformateur parfait alimentant une charge Zu soit Us = ZuIs
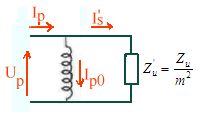
d'où tout se passe comme si on avait
Z'u = Zu/m2 directement au primaire

Si l'on tient compte de la réluctance, le reste étant supposé idéal, en circuit secondaire ouvert (is = 0) (en régime sinusoidal f = fm sin t d'où up = npmcost puisque up = npdf/dt, si Up = nm est constant il vient immédiatement que m est constant, c'est à dire indépendant de la charge)

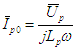pour Is = 0 ça donne or La mesure de Ip0 conduit donc à la connaissance de Rm

le schéma équivalent est alors :



cas général

On tient compte en outre des inductances de fuite et de la résistance du fil constituant les enroulements. Or à vide et d'où le schéma équivalent


avec

En ramenant toutes les fuites au primaire on obtient le schéma ci-dessous utilisé pratiquement car s peut être obtenu par une mesure en court circuit.

circuit couplé à secondaire accordé (transformateur de liaison)

Lp<< Rp

On emploie une capacité Cs



si la charge a une impédance élevée


Le circuit secondaire est équivalent à un circuit RLC dans lequel Is varie comme dans ce dipôle avec une résonance pour LsCs02 = 1

Lp # Rp

Dans ce cas l'allure générale du phénomène est la même, mais alors n'est plus négligeable et constitue un terme capacitif, ce qui entraine un décalage vers les plus hautes fréquences du maximum de Is et un affaiblissement de celui-ci.

Transformateur à primaire et secondaire accordés
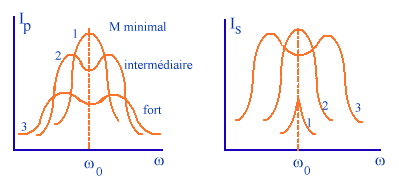
On rajoute, par rapport au cas précédent une capacité Cp en série avec le primaire de telle sorte que la résonance se produise pour la même valeur de au primaire et au secondaire. A la résonance Zs=Rs et donc est une résistance pure. Si elle est égale à Rp la transmission de puissance est maximale et le rendement atteint 50%. Ceci se produit pour un couplage moyen. Si M est faible le primaire se comporte presque comme s'il était seul, au secondaire on observe alors un maximum de Is assez pointu mais d'amplitude faible. Par contre à fort couplage les réactances ramenées entrainent une forte compensation à la résonance et donc une réduction importante de Ip à cette fréquence.



Notons que les variations de Us sont assez voisines (comme allure en 1ère approximation) de celles de Is en fonction de et du couplage.

Remarques complémentaires
Le circuit précédent peut être considéré comme un quadripôle dont le schéma équivalent serait en T



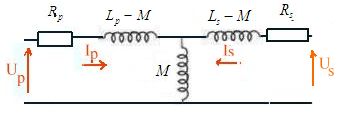
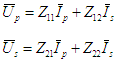On écrit alors avec

Ces équations permettent d'ailleurs de déterminer m, en effet à vide Is = 0 entraine
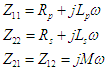
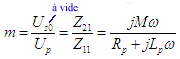
et si Rp est << Lp on a sensiblement

On peut noter aussi qu'à secondaire ouvert la relation donnant Us conduit à une détermination aisée de M puisqu'alors . Il suffit donc de mesurer Us et Ip

Notons l'existence d'une capacité parasite entre les deux enroulements qui modifie très légèrement le couplage (en l'augmentant généralement).

 Hit-Parade