Copyright
© 2000-2015 LHERBAUDIERE


5 pages à l'impression		 Hit-Parade version initiale 2000
AVERTISSEMENT dernière mise à jour
18 mars 2013
cliquez sur le mot avertissement ou information ci-dessus pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives

Méthode graphique d'étude du transformateur

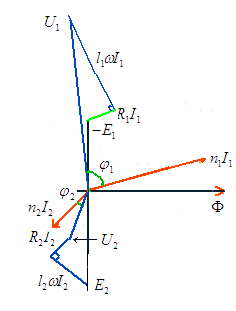
Nous allons maintenant exploiter ce qu'on appelle le diagramme du transformateur, c'est à dire l'ensemble des vecteurs représentant les grandeurs électriques et magnétiques qui entrent en jeu dans un transformateur.

cas simplifié la base
si l'on tient compte de la réluctance on complique peu à peu le modèle
et des résistances  
et des pertes magnétiques  
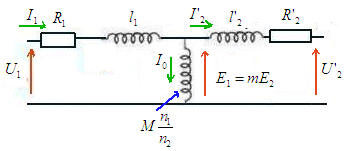
l'équation symbolique on ramène tout au primaire
diagramme de Kapp les caractéristiques du transfo
tension et impédance de court-circuit  
une collection d'icônes pour visiter tout le site
les diagrammes
Cas simplifié

La grandeur commune aux deux enroulement est le flux que l'on prendra pour origine des phases. La variation périodique de flux engendrant dans le primaire une fem E1 et dans le secondaire une fem E2 déphasées de /2 en retard sur le flux.

Dans le cas simplifié du transformateur parfait on a vu

- E1 = U1 U2 = E2 n1I1 = - n2I2

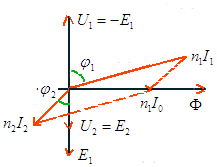
Si j'appelle 2 le déphasage entre U2 et I2, il vient 1 = 2, d'où le diagramme (1)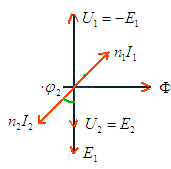


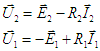diagramme (1)
Si l'on tient compte de la réluctance

le courant à vide est en phase avec F d'où le diagramme (2)



Si l'on tient compte des résistances des enroulements

d'où le diagramme (3)

Si les pertes dans le fer sont non nulles :

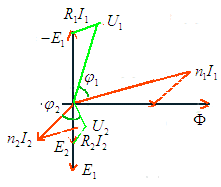
n1I0 n'est plus en phase avec (le déphasage est < /2). La puissance active dépensée à vide qui n'est plus nulle s'exprime par U1I0cos0 et correspond aux pertes dans le fer



fuites magnétiques

et de même

si l'on ramène tout au primaire

On aboutit alors au schéma symbolique équivalent



l'équation des volts secondaires est



Si dans cette expression on remplace E1 par sa valeur tiée de l'équation primaire on aboutit à l'équation symbolique du transformateur déjà rencontrée



on en déduira le diagramme simplifié de Kapp.

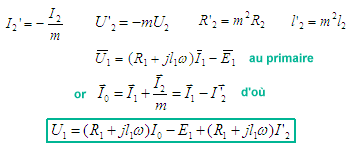
caractéristiques du transformateur
rapport de transformation et chute de tension en charge

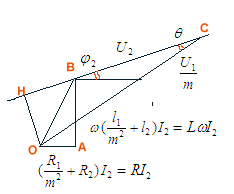
rapport nominal m (U1 au primaire et U1/m au secondaire à vide)

U1/U2 = rapport en charge d'où U1/m - U2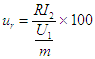 = chute de tension en charge

Pour la définir on utilise le diagramme de Kapp

En fait il s'agit d'une simplification du cas général supposant I0 (à vide) = 0, dans ces conditions l'équation symbolique devient et la représentation vectorielle dite diagramme de Kapp



R représente la résistance ramenée au primaire, L l'inductance de fuite ramenée au primaire. Ce diagramme ne permet évidemment pas de déterminer I1 et 1, mais seulement la chute de tension. Il suppose aussi des pertes fer réduites.

Le triangle OAB est défini par une mesure en court circuit donnant I2 (avec un simple ampèremètre), on mesure U1cc correspondant, alors U2 = 0 et C vient en B donc OB = U1cc/m. R étant mesuré de même que I2 donc OA est connu.

La mesure de U2 pour un certain I2 permet de déterminer 2 (phase de I2 par rapport à U2) selon une relation du type U2 = ZuI2 et donc graphiquement U1/m et la chute de tension U1/m - U2

Graphiquement cette chute de tension en 1ère approximation est équivalent à BH, or soit en posant chute résistive en % et 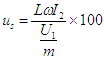chute inductive en %, il vient la chute de tension relative en %

tension et impédance en court circuit

En divisant les 3 vecteurs du diagramme de Kapp par U1/m on obtient en %

ucc exprime (en % de la tension nominale) la tension qu'il faut appliquer à un enroulement pour que l'autre débite en court-circuit son courant nominal.

La tension de court-circuit en % étant (U1n étant la tension primaire nominale), l'impédance de court-circuit côté primaire sera donc soit encore

côté secondaire c'est

Rendement

En fait P1 = P2 + pertes joule + pertes fer.

 Hit-Parade