
Copyright
© 2000-2015
LHERBAUDIERE
5 pages à l'impression

18 mars 2013
 |
Copyright |
5 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
Systèmes polyphasés
| définition | la multiplication des...fem | |||
| production d'une fem polyphasée | un principe simple | |||
| intérêt pratique | comment faire des économies de cuivre | |||
| système triphasé industriel | parlons de l'EdF | |||
| puissance des systèmes polyphasés | la mesure | |||
| une collection d'icônes pour visiter tout le site | ||||
 et supposons les décalées
de 120 degrés. D'après ce qui précède aux bornes
de chacune d'elles on aura une fem de même valeur maximale mais déphasées
respectivement de 2
et supposons les décalées
de 120 degrés. D'après ce qui précède aux bornes
de chacune d'elles on aura une fem de même valeur maximale mais déphasées
respectivement de 2 /3 et de 4
/3 et de 4 /3
c'est à dire :
/3
c'est à dire :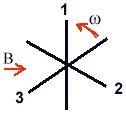 ;
;;;;;
;
;;;;;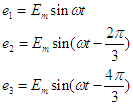
 /3
l'un par rapport à l'autre.
/3
l'un par rapport à l'autre. /n et n récepteurs
identiques nous aurions un système n-phasé équilibré.
/n et n récepteurs
identiques nous aurions un système n-phasé équilibré. /n et constituant le n-ième générateur
d'un circuit n-phasé.
/n et constituant le n-ième générateur
d'un circuit n-phasé.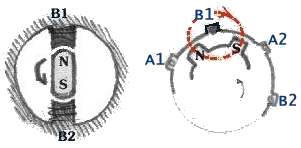
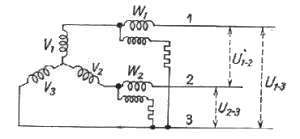
 étoilé
étoilé 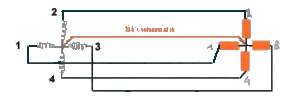
 polygonal
polygonal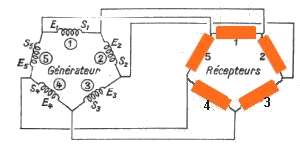
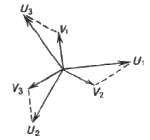
 relations
du montage étoile
relations
du montage étoile
 .........
.........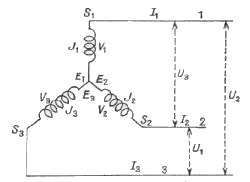

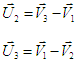 d'où on déduit U1 = 2V1 cos (
d'où on déduit U1 = 2V1 cos ( /6)
= 31/2 V1
/6)
= 31/2 V1 montage
polygonal (ou triangle) triphasé
montage
polygonal (ou triangle) triphasé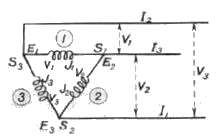
 /6). Les courants de ligne
sont racine de trois fois ceux de phase et décalés de
/6). Les courants de ligne
sont racine de trois fois ceux de phase et décalés de  /6
par rapport à ceux-ci.
/6
par rapport à ceux-ci. nécessité
pratique du fil neutre dans les réseaux de distribution
nécessité
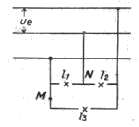
pratique du fil neutre dans les réseaux de distribution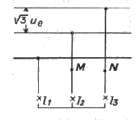 .......
.......
 expression
générale de la puissance active d'un système triphasé
expression
générale de la puissance active d'un système triphasé
 système
triphasé équilibré
système
triphasé équilibré


 puissance
réactive
puissance
réactive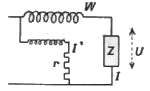

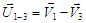
 /6 -
/6 -  et W2 = U I cos (
et W2 = U I cos ( /6 +
/6 +  )
) /6
cos
/6
cos = 31/2 U I cos
= 31/2 U I cos
 = 1 soit
= 1 soit  = 0 on a W1 = W2 on dit que le facteur de puissance
est égal à 1
= 0 on a W1 = W2 on dit que le facteur de puissance
est égal à 1 = 0.5 l'un des deux wattmètre
donne une déviation nulle.
= 0.5 l'un des deux wattmètre
donne une déviation nulle. |