log2

Copyright
© 2000-2015 LHERBAUDIERE


6 pages à l'impression		 Hit-Parade version initiale 2000
AVERTISSEMENT dernière mise à jour
18 mars 2013
cliquez sur le mot avertissement pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives

Algèbre de Boole - Simplification des Fonctions Logiques (2/9)

fonctions logiques et relations temporelles chronogramme
théorèmes et relations de Morgan
écriture canonique d'une fonction produits ou sommes
simplification d'une fonction logique problème de redondance
tableaux de Karnaugh un procédé graphique
logigramme d'une fonction booléenne un exemple
une collection d'icônes pour visiter tout le site
1.3 fonctions logiques et relations temporelles

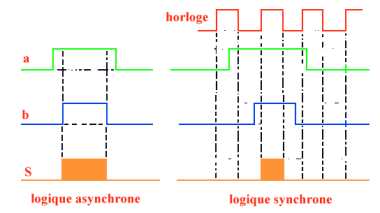
Soit une porte ET à deux entrées a et b, on distinguera 2 types de logique :
1.4. Théorèmes et relations

Les plus célèbres, qu'on a déjà implicitement rencontrées, sont dues à De Morgan on peut les écrire sous la forme :

( a . b) barre = a barre + b barre et inversement ( a + b ) barre = a barre . b barre

soit l'inverse d'une réunion est égal à l'intersection des inverses et réciproquement. Ces relations ont été généralisées par Shannon :
f(a,b,c +, . ) barre = f ( a barre, b barre, c barre, ., +). Cette dernière formulation est à utiliser avec précaution, on remplace les variables par leurs inverses et les opérateurs OU par ET et vice versa, mais attention. Prenons par exemple la fonction f = x + y barre z

on aura f barre = ( x + y barre z) barre qui n'est pas x barre y + z barre, mais en posant (y barre z) = A
on obtient f barre = (x + A) barre = x barre . A barre soit x barre ( y + z barre) = x barre y + x barre z barre
propriétés remarquables :
a + a = a a + a barre = 1
a . a = a a . a barre = 0
a + 1 = 1 a + 0 = a
a . 1 = a a . 0 = 0
quelques théorèmes parfois utiles
a + (a . b) = a

a + (a barre . b) = a + b = x avec la table de vérité suivante

a b a barre b x
1 1 0 1
1 0 0 1
0 1 1 1
0 0 0 0
1.5. écriture canonique d'une fonction logique
fonctions produits
Soient 3 variables a, b , c on peut définir les huits combinaisons de type P = abc représentées dans le tableau ci-dessous. Avec la convention d'écriture suivante les variables barres, en l'absence de la possibilité de surlignage en HTML, seront écrites en rouge, dans la première colonne (jaune) figurent les valeurs de chacune des trois variables tandis que dans les huit colonnes de droite figurent les valeurs des produits. Pour des raisons de clarté nous n'avons fait figurer que les produits égaux à 1

  P0 P1 P2 P3 P4 P5 P6 P7
abc abc abc abc abc abc abc abc abc
000 1              
001   1            
010     1          
011       1        
100         1      
101           1    
110             1  
111               1

Soit une fonction f quelconque des 3 variables a, b et c. On va constater (par exemple) que cette fonction vaut 1 en même temps que P1, P3 et P4. On va écrire :

f = P1 + P3 +P4 = abc + abc + abc cette somme est dite somme canonique de produits

fonction sommes
Mais on peut aussi exprimer les sommes du type S = a + b + c qui conduisent, avec la même convention d'écriture, au tableau suivant où seuls les zéros sont écrits.

  S0 S1 S2 S3 S4 S5 S6 S7
abc a+b+c a+b+c a+b+c a+b+c a+b+c a+b+c a+b+c a+b+c
000 0              
001   0            
010     0          
011       0        
100         0      
101           0    
110             0  
111               0

On constatera par exemple qu'une fonction f vaudra 0 en même temps que S1, S2 et S8 et on pourra alors écrire que la fonction peut s'écrire sous la forme d'un produit canonique de sommes f = (a+b+c) (a+b+c) (a+b+c)

1.6. simplification d'une fonction logique

La représentation d'une fonctionn logique par une forme canonique n'est généralement pas la façon la plus condensée d'écrire l'équation représentative d'un problème. Il peut y avoir redondance, c'est à dire risque d'utilisation de plus de composants qu'il n'en faut pour réaliser électroniquement cette fonction. Ce fut d'ailleurs typiquement le problème de Shannon lorsqu'il s'intéressa au problème des contacts de relais téléphoniques. Des contacts inutiles ne nuisent pas au bon fonctionnement du réseau, mais, économiquement, ils accroissent les coûts de l'équipement.


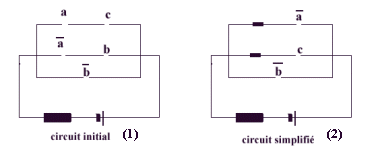
Pour illustrer ce problème considérons un ex, déjà simplifié, représenté par la fonction f = a.c + a.b + b qui schématiquement pourrait être représentative du circuit (1) . En vertu des théorèmes précités a.b + b = a + b

soit f = a.c + a + b ce qui peut encore se réduire, en vertu du même théorème, en f = a + c + b et conduit au schéma simplifié (2).

1.7. tableaux de Karnaugh

Pour simplifier le casse tête des tables de vérité dans les cas de fonctions de plusieurs variables on peut utiliser la technique de représentation graphique imaginée par Karnaugh qui permet des simplifications assez aisées.

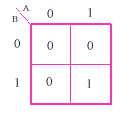
ainsi par ex : x = a.b dont la table de vérité ci-dessous peut se représenter selon le graphique de droite

a b x  
0 1 0  
1 0 0  
0 0 0  
1 1 1  

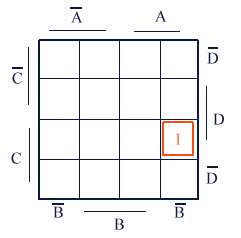
où le carré rose représente les valeurs de x, correspondant aux valeurs des variables A et B, figurées à l'extérieur. Une première simplification apportée par ce diagramme va consister à ne faire figurer que les 1 dans le tableau, ce qui allège considérablement l'écriture et la lisibilité. Ainsi par ex la fonction X = ABCD


Utilisation pour exprimer la forme canonique d'une fonction. On va encore prendre l'exemple d'une fonction de 4 variables, avec toujours la convention typographique A barre écrit A:

Soit X = ABCD + ABCD + ABCD + ABCD

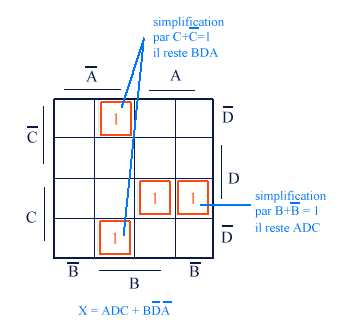
La procédure est la suivante : on représente le graphe comme ci-dessus, puis on écrit tous les 1 de la fonction x. Enfin on en déduit toutes les simplifications correspondant à deux 1 contigüs. En effet deux 1 contigus indiquent une mise en facteur possible du type Y+Y = 1


Un conseil : toujours représenter le diagramme de Karnaugh de la même façon, comme ici par exemple, cela procure un gain de temps. Dans le cas d'une fonction à cinq variables, comme le dessin risque d'être un peu compliqué, on préférera représenter plusieurs diagrammes à 4 variables l'un pour ABCD et E et l'autre pour ABCD et E, etc. On trouve des logiciels qui permettent ces représentations et l'immédiateté des simplifications.

1.8. Logigramme d'une fonction booléenne.

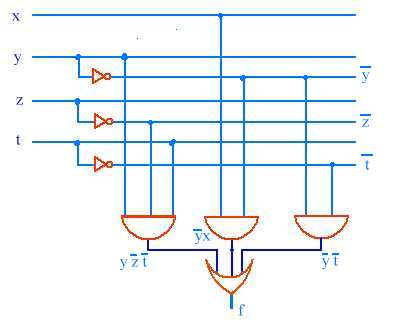
Il s'agit de la traduction en opérateurs élémentaires de la fonction mise sous sa forme simplifiée, obtenue soit par Karnaugh soit par manipulation mathématique. Soit l'exemple f = y z t + x y + y t que l'on veut représenter avec des ET/OU/NON.
Procédure : on détermine le nombre de variables maxi, car il faut penser dans une réalisation pratique que la sortance (ou l'entrance) d'un circuit n'est pas illimitée. Rappelons que la sortance est le nombre de boitiers de la même famille que l'on peut connecter en parallèle à la sortie d'un circuit). Ici il n'y aura pas de problème puisqu'on aura au maximum 3 entrées sur un élément.

Hit-Parade