log1

Copyright
© 2000-2015 LHERBAUDIERE


5 pages à l'impression		 Hit-Parade version initiale 2000
AVERTISSEMENT dernière mise à jour
18 mars 2013
cliquez sur le mot avertissement pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives utiles pour vos études, ne pas le faire par paresse serait franchement idiot.
Dans les chapitres qui suivent nous avons rassemblé les bases de la logique, non pour créer un cours d'électronique numérique supplémentaire, car il en existe déjà beaucoup sur le web, mais simplement pour permettre au lecteur de ce site, soit de se remémorer, soit de découvrir quelques éléments essentiels pour la compréhension du fonctionnement du microprocesseur et des circuits sophistiqués qui lui sont associés et dont nous parlons longuement dans le module suivant. Enfin ces éléments ont aussi pour objectif de permettre la compréhension fine de la structure d'une chaîne instrumentale.
Algèbre de Boole - Fonctions Logiques

variables binaires et règles de calcul des règles simples
fonctions logiques fonctions basiques de l'info
  une collection d'icônes pour visiter tout le site
1. L'algèbre de Boole

Lorsque George Boole imagina les concepts élémentaires de ce qui allait devenir l'algèbre de Boole il ne pensait qu'à un divertissement de l'esprit et ne pouvait alors deviner quelle importance fantastique cela allait prendre un siècle plus tard. En fait c'est dès 1938 que l'américain Shannon , peut-être précédé par les japonais Nakasima et Hanzava, s'aperçoit que cette algèbre pouvait aider à la rationalisation des relais téléphoniques. Les bases de cette nouvelle algèbre sont extrêmement simples.
1.1 variables binaires / règles de calcul fondamentales.
Une variable binaire ne peut prendre que deux états, vrai ou faux, symbolisés conventionnellement par 1 ou 0. Si a est une telle variable, écrire que a = 0 implique a différent de 1. Pour l'électronicien c'est une définition très intéressante qui entraine une très grande fiabilité. En effet la séparation théorique entre les deux états 1 et 0 pourra être caractérisée par une certaine valeur d'un potentiel, en pratique une certaine amplitude d'une impulsion. Mais les zones qui caractérisent ces deux états peuvent s'étendre indéfiniment en deçà ou au delà de la limite. Ainsi par exemple, 0 représentera toute tension, appliquée sur la base d'un transistor NPN en émetteur commun, ne le débloquant pas (donc négative, nulle, voire faiblement positive) tandis que l'état 1 sera toute tension positive l'amenant à saturation. Typiquement, dans la famille de composants dits TTL un zéro caractérisera toute tension < 0.8V et 1 correspondra à >2V (alimentation typique =+5V dans les années 80 et souvent 3V et parfois moins dans les circuits récents).

Les postulats de base de l'algèbre de Boole sont les suivants :

0 x 0 = 0 0 + 1 = 1
0 x 1 = 0 1 + 1 = 1
1 x 0 = 0 1 + 0 = 1
1 x 1 = 1 0 + 0 = 0

Ces postulats de base, dont certains ressemblent à l'algèbe classique vont se traduire par des fonctions binaires. Et les machines de traitement de l'information, ordinateurs par exemple, vont en pratique à partir de variables d'entrée binaires calculer des fonctions de sortie binaires. Précisons que le nombre de variables d'un problème réel donné peut être très élevé, ça ne change évidemment rien aux postulats ci-dessus (0+1+1+0+1=1 évidemment, etc...).

Notons que ces fonctions binaires se rencontrent dans la vie courante : Ainsi un automobiliste va ralentir s'il y a un panneau de limitation de vitesse ET s'il est discipliné OU s'il voit un képi de gendarme OU si son GPS lui rappelle cette limitation..

1.2. Fonctions logiques
Il existe 3 fonctions de base dont découlent, par combinaison, toutes les autres : NON / ET / OU

Nous allons les illustrer par des exemples pédagogiques les plus simples avec le minimum possibles d'entrées pour une meilleure compréhension, sachant qu'évidemment dans les dispositifs technologiques la réalité peut être infiniment plus complexe, mais n'est jamais qu'une combinaison des dispositifs les plus simples. Rappelons qu'en électronique on a imaginé un dispositif élémentaire appelé amplificateur et qui dispose de 2 entrées et d'une seule sortie accessible et selon l'entrée exploitée le signal de sortie est semblable ou inversé par rapport à celui d'entrée. C'est la même idée élémentaire qui va être exploitée (mais dans une réalisation technologique simplifiée) et en combinant n dispositifs élémentaires on réalisera des systèmes extrêment complexes, tel un microprocesseur par exemple qui représente le cas extrême, avec éventuellement un grand nombre d'entrées et plusieurs sorties.
NON (encore appelée complément ou inverse) f(x) = x barre. Si x = 0 alors NON x = 1 et inversement . Rappelons que nous appelons a barre la quantité inverse de a que l'on note aussi dans les ouvrages ou au tableau
table de vérité relations caractéristiques
E S a + a barre = 1
0 1 a x a barre = 0
1 0 (a barre) barre = a

Technologiquement la fonction NON est réalisée via un circuit inverseur.

.....
rappelons pour mémoire la structure des composants MOS

fonction OU (inclusion, réunion, notée +)
f(x,y) = x + y ce qu'en mathématiques on note généralement f(x,y) = x U y

C'est une fonction de plusieurs variables par ex a, b, c qui sera égale à 1 si l'une au moins des variables est égale à 1
table de vérité
a 0 0 0 1 1 1 1 0
b 1 0 0 1 0 1 0 1
c 1 0 1 1 0 0 1 0
f 1 0 1 1 1 1 1 1
symbole et technologie
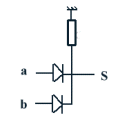  si a ou b < 0 une diode est passante .alors S = 1 .. structure NMOS
  logique négative logique positive
fonction ET (intersection, notée x ou .)
f(a,b) = a . b
table de vérité
a 0 1 1 0
b 0 0 1 1
f 0 0 1 0


En dehors de ces trois fonctions élémentaires, il y a quelques fonctions complémentaires qui sont technologiquement plus simples à réaliser, en pariculier en technologie N-MOS ce qui est évidemment économiquement très intéressant. Ainsi par exemple la fonction NI ou NON/OU ou NOR en anglais qu'on note parfois OU barre.

à laquelle correspond la table de vérité suivante, et un circuit dérivé du OU moins un inverseur
a 0 0 1 1
b 0 1 0 1
f 1 0 0 0
S = 1 si ni a ni b ne sont égaux à 1
fonction NON/ET, NAND ou ET barre
comme le circuit précédent sa technologie correspond au circuit ET auquel on a enlevé un inverseur

a 0 0 1 1
b 1 0 1 0
f 1 1 0 1
fonction OU exclusif
: S = 1 si a ou b , mais pas les deux, sont égaux à 1

.....
table de vérité
a 0 0 1 1
b 0 1 1 0
f 0 1 0 1
fonction coïncidence : c'est l'inverse du ou exlusif
a 0 0 1 1
b 0 1 1 0
S 1 0 1 0

S = 1 si a = b

A partir de ces fonctions simples on peut réaliser toutes les combinaisons telles celles ci-dessous :

a 0 0 0 0 1 1 1 1
b 0 1 0 1 0 1 0 1
c 0 1 1 0 0 1 1 0
S 1 1 1 1 0 0 0 0
qui correspond à la fonction

ou celle-ci dite inhibition
qui correspond par exemple à la proposition suivante : pour démarrer une voiture il faut que le moteur (a) tourne ET qu'une vitesse (b) soit enclenchée ET que le frein à main (c) ne soit PAS serré.


chronogrammes donnant les différents signaux en fonction du temps

En logique synchrone la sortie est synchronisée par l'horloge, c'est la même chose pour tous les circuits ayant une entrée H (parfois appelée clock et notée CK). L'utilité d'une telle synchronisation est essentielle dès lors qu'on va disposer de voies parallèles ayant un nombre de portes différents pour resynchroniser ces voies parallèles et réduire le risque de sorties aléatoires. De même les parasites qui pourraient être pris en compte et simuler des niveaux 1 seront moins génants dans les circuits synchrones puisqu'en dehors de H = 1 ils ne peuvent être pris en compte. Ainsi si la durée de H = 1 est très inférieure à celle de H = 0 le risque de perturbations par des parasites de courte durée peut être fortement réduit, sans toutefois être totalement éliminé.

 Hit-Parade