
Copyright
© 2000-2015
LHERBAUDIERE
3 pages à l'impression

18 mars 2013
 |
Copyright |
3 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
moteur synchrone
| équation du moteur synchrone | ||||
| propriétés du moteur synchrone | ||||
| une collection d'icônes pour visiter tout le site | ||||
 va
engendrer deux ensembles de pôles fictifs tournant dans des sens opposés
à la vitesse
va
engendrer deux ensembles de pôles fictifs tournant dans des sens opposés
à la vitesse  /p.
/p. /p
et son effet sera fortement atténué du fait de l'écran
électrodynamique constitué soit par les pôles massifs de
l'inducteur, soit par des amortisseurs (pour réduire les courants de
Foucauld et la réaction d'induit), par voie de conséquence le
moteur synchrone monophasé ne diffère pas du triphasé et
c'est lui que nous allons prendre comme modèle.
/p
et son effet sera fortement atténué du fait de l'écran
électrodynamique constitué soit par les pôles massifs de
l'inducteur, soit par des amortisseurs (pour réduire les courants de
Foucauld et la réaction d'induit), par voie de conséquence le
moteur synchrone monophasé ne diffère pas du triphasé et
c'est lui que nous allons prendre comme modèle. I
I
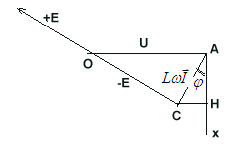
 = L
= L I
cos
I
cos = ( L
= ( L /U) UIcos
/U) UIcos donc le vecteur AH à chaque instant représente (U et L
donc le vecteur AH à chaque instant représente (U et L étant constant) à une échelle convenable la puissance absorbée
par le moteur Pa
étant constant) à une échelle convenable la puissance absorbée
par le moteur Pa vitesse angulaire du moteur, et il peut lui
aussi être représenté par AH avec une autre échelle.
vitesse angulaire du moteur, et il peut lui
aussi être représenté par AH avec une autre échelle.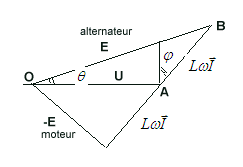 |
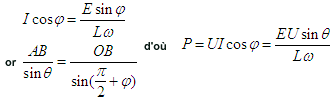 |
 (c'est à dire
du déphasage de E par rapport à U) ce qu'on avait déjà
montré précédemment.
(c'est à dire
du déphasage de E par rapport à U) ce qu'on avait déjà
montré précédemment. <
<  /2 un ralentissement correspond à
une augmentation du couple moteur, c'est le régime stable.
Précisons que
/2 un ralentissement correspond à
une augmentation du couple moteur, c'est le régime stable.
Précisons que  correspond à
correspond à
 décalage mécanique vu dans le
chapitre précédent.
décalage mécanique vu dans le
chapitre précédent. /2 <
/2 <  <
<
 le ralentissement se traduit par une diminution
du couple donc marche instable.
le ralentissement se traduit par une diminution
du couple donc marche instable. et
et  sont identiques. Initialement le point de fonctionnement est P1 et
on devrait du fait de la surcharge atteindre P2. Pour ce faire la
roue polaire ralentit et perd une énergie cinétique
sont identiques. Initialement le point de fonctionnement est P1 et
on devrait du fait de la surcharge atteindre P2. Pour ce faire la
roue polaire ralentit et perd une énergie cinétique

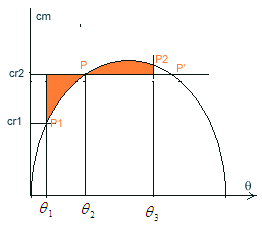
 2 le
couple moteur devient supérieur au couple résistant et dès
lors tout en restant au dessous de la vitesse de synchronisme la roue polaire
reprend de la vitesse, elle ne devient supérieure à la vitesse
de synchronisme que lorsqu'elle a repris l'énergie
2 le
couple moteur devient supérieur au couple résistant et dès
lors tout en restant au dessous de la vitesse de synchronisme la roue polaire
reprend de la vitesse, elle ne devient supérieure à la vitesse
de synchronisme que lorsqu'elle a repris l'énergie  / L
/ L est maximum pour sin
est maximum pour sin = 1, on voit donc l'utilité
de réduire L = F/I et donc le flux (qui dépend de la réluctance
et donc de l'entrefer).
= 1, on voit donc l'utilité
de réduire L = F/I et donc le flux (qui dépend de la réluctance
et donc de l'entrefer).|
|
 |