
Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression

18 mars 2013
 |
Copyright |
6 pages à l'impression |
 |
version initiale 2000 | |
| dernière
mise à jour 18 mars 2013 |
Machines à courant alternatif
| inductions tournantes | comment réaliser un champ tournant | |||
| action sur un aimant | le principe du moteur synchrone | |||
| fem induites par le mouvement de l'aimant | et de son inverse l'alternateur | |||
| action sur un circuit fermé | le moteur asynchrone | |||
| cas de 2 inductions | le moteur asynchrone monophasé | |||
| une collection d'icônes pour visiter tout le site | ||||
 /2 par rapport à l'autre. Soient les
courants i1 = Isin
/2 par rapport à l'autre. Soient les
courants i1 = Isin t et i2
= Icos
t et i2
= Icos t et supposons qu'ils parcourent deux
bobines B1 et B2 semblables produisant en un point O des
champs magnétiques perpendiculaires. La bobine B1 produit
en O un champ H1 proportionnel à l'intensité i1
que l'on peut écrire H1= Gi1 = GIcos
t et supposons qu'ils parcourent deux
bobines B1 et B2 semblables produisant en un point O des
champs magnétiques perpendiculaires. La bobine B1 produit
en O un champ H1 proportionnel à l'intensité i1
que l'on peut écrire H1= Gi1 = GIcos t
ce champ est dirigé suivant Ox. La bobine B2 située
à la même distance de O que B1 produit un champ H2
= GIsin
t
ce champ est dirigé suivant Ox. La bobine B2 située
à la même distance de O que B1 produit un champ H2
= GIsin t dirigé suivant Oy.
t dirigé suivant Oy.
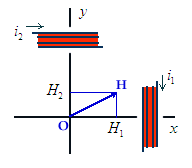
 =
=  t
(argument de H).
t
(argument de H). égale
à la pulsation des courants (fréquence = nombre de tr/s). Un tel
champ est dit champ tournant. L'induction correspondante
a aussi une intensité constante et elle tourne avec la même vitesse
angulaire.
égale
à la pulsation des courants (fréquence = nombre de tr/s). Un tel
champ est dit champ tournant. L'induction correspondante
a aussi une intensité constante et elle tourne avec la même vitesse
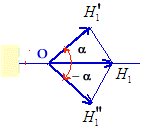
angulaire. t. On peut considérer que le
vecteur H1 est la somme de 2 vecteurs H'1 et H"1
de longueur GI/2 et tournant autour de O avec une vitesse angulaire respectivement
t. On peut considérer que le
vecteur H1 est la somme de 2 vecteurs H'1 et H"1
de longueur GI/2 et tournant autour de O avec une vitesse angulaire respectivement
 et -
et - . On
peut donc dire que H1 est la résultante
de 2 champs tournants H'1 et H"1.
. On
peut donc dire que H1 est la résultante
de 2 champs tournants H'1 et H"1.
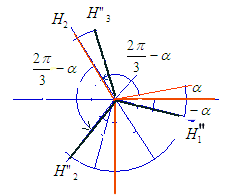
 , tandis
que les H" tournent avec -
, tandis
que les H" tournent avec - mais sont
eux décalés de 2
mais sont
eux décalés de 2 /3. Sur le graphique
on voit donc que leur somme est nulle. Il en résulte que H = 3GI/2
avec un angle
/3. Sur le graphique
on voit donc que leur somme est nulle. Il en résulte que H = 3GI/2
avec un angle  =
=  t.
C'est un champ tournant dans le sens positif.
t.
C'est un champ tournant dans le sens positif.
 0 (positive)
créée par des courants polyphasés de fréquence f0
=
0 (positive)
créée par des courants polyphasés de fréquence f0
= 0/2
0/2 ,
on place un aimant permanent de moment magnétique
,
on place un aimant permanent de moment magnétique 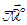 .
. (de signe quelconque) affectons d'un indice
0 les valeurs de l'induction et du moment magnétique à l'instant
t = 0 décalés d'un angle
(de signe quelconque) affectons d'un indice
0 les valeurs de l'induction et du moment magnétique à l'instant
t = 0 décalés d'un angle  et
considérons la situation à un instant t quelconque. Entre les
4 vecteurs on va avoir les angles :
et
considérons la situation à un instant t quelconque. Entre les
4 vecteurs on va avoir les angles :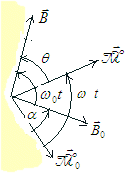 |
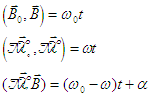 |
 dont la valeur, comptée positivement
dans le sens de la rotation du champ, est
dont la valeur, comptée positivement
dans le sens de la rotation du champ, est  0 et
0 et  sont différents ce couple va être alternativement positif et négatif,
c'est à dire moteur ou résistant.
Sa valeur moyenne est nulle et il ne fournit au total aucun travail.
sont différents ce couple va être alternativement positif et négatif,
c'est à dire moteur ou résistant.
Sa valeur moyenne est nulle et il ne fournit au total aucun travail. de même signe que
de même signe que  0
mais
0
mais  <
<  0
ou bien de signes opposés. Si aucune source d'énergie n'entretient
le mouvement du fait des frottements la vitesse va diminuer
progressivement et l'aimant va finir par s'arrêter.
0
ou bien de signes opposés. Si aucune source d'énergie n'entretient
le mouvement du fait des frottements la vitesse va diminuer
progressivement et l'aimant va finir par s'arrêter. >
>  0
et de même sens. Dans un premier temps on va constater le même phénomène
0
et de même sens. Dans un premier temps on va constater le même phénomène
 va diminuer jusqu'à l'égalité
avec
va diminuer jusqu'à l'égalité
avec  0 alors
0 alors  est constant
est constant  est compris entre 0 et
est compris entre 0 et  on a
on a  > 0 soit couple
moteur.
> 0 soit couple
moteur. = 0 et le retard entre l'aimant et l'induction est donc nul. Si les frottements
viennent à augmenter alors
= 0 et le retard entre l'aimant et l'induction est donc nul. Si les frottements
viennent à augmenter alors  augmente
ce qui tend à ralentir l'aimant et donc à augmenter a jusqu'à
rétablir l'équilibre. On voit donc que lorsque la charge va augmenter
seul le décalage a entre l'induction et l'aimant va augmenter tant que
augmente
ce qui tend à ralentir l'aimant et donc à augmenter a jusqu'à
rétablir l'équilibre. On voit donc que lorsque la charge va augmenter
seul le décalage a entre l'induction et l'aimant va augmenter tant que
 <
<  /2. Par
contre dès que
/2. Par
contre dès que  >
>  /2
la vitesse va diminuer et le couple moteur aussi et, in fine, le moteur
va décrocher et s'arrêter. Il y a
donc une charge maxi à ne pas dépasser.
/2
la vitesse va diminuer et le couple moteur aussi et, in fine, le moteur
va décrocher et s'arrêter. Il y a
donc une charge maxi à ne pas dépasser. est à chaque instant égal à l'énergie électrique
absorbée par les forces contre électromotrices.
est à chaque instant égal à l'énergie électrique
absorbée par les forces contre électromotrices. de
ce mouvement sur le champ, lorsque la charge varie la variation correspondante
de la puissance électrique consommée dans chaque circuit provient
de la variation du facteur de puissance :
de
ce mouvement sur le champ, lorsque la charge varie la variation correspondante
de la puissance électrique consommée dans chaque circuit provient
de la variation du facteur de puissance : =
=  /2, la puissance consommée est maximale,
la fem d'induction est en opposition de phase avec le courant, c'est à
dire que leur déphasage est
/2, la puissance consommée est maximale,
la fem d'induction est en opposition de phase avec le courant, c'est à
dire que leur déphasage est  et cos
et cos =
-1. Quand la charge diminue, cos
=
-1. Quand la charge diminue, cos diminue en
valeur absolue et quand le moteur tourne à vide et que la puissance consommée
est nulle (en négligeant les frottements) alors la fem est en quadrature
avec le courant.
diminue en
valeur absolue et quand le moteur tourne à vide et que la puissance consommée
est nulle (en négligeant les frottements) alors la fem est en quadrature
avec le courant. 0,
les fem induites dans les bobines sont inchangées, et l'appareil fonctionne
alors comme alternateur polyphasé (dans
les bobines et dans les circuits sur lesquels elles sont refermées s'établit
alors un système de courants polyphasés). Le mouvement de l'aimant
est alors en avance sur le champ tournant créé par le passage
des courants dans les bobines et le couple électromagnétique G
est alors un couple résistant.
0,
les fem induites dans les bobines sont inchangées, et l'appareil fonctionne
alors comme alternateur polyphasé (dans
les bobines et dans les circuits sur lesquels elles sont refermées s'établit
alors un système de courants polyphasés). Le mouvement de l'aimant
est alors en avance sur le champ tournant créé par le passage
des courants dans les bobines et le couple électromagnétique G
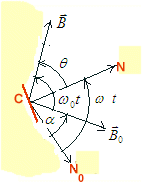
est alors un couple résistant.| moteur synchrone | alternateur | : machine sensiblement réversible |
sin  > 0 > 0 |
sin  < 0 < 0 |
|
cos  < 0 < 0 |
cos  > 0 > 0 |
 0.
On place un circuit plan en O de surface S de résistance r et de self
L susceptible de tourner autour de l'axe O avec une vitesse angulaire
0.
On place un circuit plan en O de surface S de résistance r et de self
L susceptible de tourner autour de l'axe O avec une vitesse angulaire  .
Sur ce circuit on définit un sens positif pour compter les fem et les
courants, il en résulte du fait de la règle d'Ampère un
sens positif pour la normale au plan du circuit ON. L'angle (ON, B) à
l'instant t compté dans le sens positif de rotation du champ est (
.
Sur ce circuit on définit un sens positif pour compter les fem et les
courants, il en résulte du fait de la règle d'Ampère un
sens positif pour la normale au plan du circuit ON. L'angle (ON, B) à
l'instant t compté dans le sens positif de rotation du champ est ( 0
-
0
-  )t +
)t +  avec les mêmes conventions que précédemment. Le flux de
B à travers le circuit est
avec les mêmes conventions que précédemment. Le flux de
B à travers le circuit est  et la fem induite dans ce circuit
et la fem induite dans ce circuit  0
-
0
-  produisant dans le circuit C un courant
de même pulsation
produisant dans le circuit C un courant
de même pulsation  (loi d'Ohm dans un circuit rL)
(loi d'Ohm dans un circuit rL) 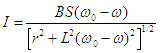 et
et  = BiSsin
= BiSsin
 /(
/( 0
-
0
-  ),
),  varie
de
varie
de  à 2
à 2 +
+  et la valeur moyenne de cos (2
et la valeur moyenne de cos (2 -
-  ) est nulle et la valeur moyenne du couple
moteur s'exprime par
) est nulle et la valeur moyenne du couple
moteur s'exprime par 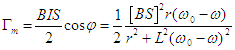
 <
<  0)
il est soumis à un couple moteur de valeur moyenne non nulle, il peut
fournir du travail : c'est le principe des moteurs asynchrones
dans lesquels le circuit mobile ne reçoit aucun courant de l'extérieur
0)
il est soumis à un couple moteur de valeur moyenne non nulle, il peut
fournir du travail : c'est le principe des moteurs asynchrones
dans lesquels le circuit mobile ne reçoit aucun courant de l'extérieur
 0 -
0 - )
soit en faisant
)
soit en faisant  M
donné par
M
donné par  = - µ, passe par un max pour
= - µ, passe par un max pour  M
=
M
= 0 - r/L, puis décroit jusqu'à
zéro pour
0 - r/L, puis décroit jusqu'à
zéro pour  =
=  0
ensuite on a une branche de courbe symétrique.
0
ensuite on a une branche de courbe symétrique.
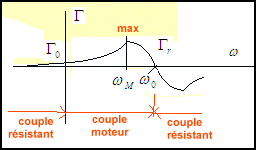
 0
lorsque le moteur est arrêté il est soumis à
0
lorsque le moteur est arrêté il est soumis à  0
(
0
( = 0) et donc le moteur se met en mouvement,
= 0) et donc le moteur se met en mouvement,
 augmente, de même que le couple jusqu'à
ce que
augmente, de même que le couple jusqu'à
ce que  M=
M=  r
et on a alors un fonctionnement stable dans la plage
r
et on a alors un fonctionnement stable dans la plage  M
M
 0 car à toute augmentation
de
0 car à toute augmentation
de  r tendant à ralentir
le moteur correspond un accroissement de
r tendant à ralentir
le moteur correspond un accroissement de  M
stabilisant la vitesse à une valeur peu différente.
M
stabilisant la vitesse à une valeur peu différente. r
=
r
= 
 0 mais de sens inverses, à
l'instant t B et B' font avec B0 les angles
0 mais de sens inverses, à
l'instant t B et B' font avec B0 les angles  =
< 0 = t et -
=
< 0 = t et - 0t et avec la normale
au circuit les angles
0t et avec la normale
au circuit les angles  ,
, '
en considérant les 2 inductions séparément (théorème
de superposition)
'
en considérant les 2 inductions séparément (théorème
de superposition) =
SiBsin
=
SiBsin + Si'B'sin
+ Si'B'sin '
et le couple moyen
'
et le couple moyen  m somme des
2 couples moyen que produiraient ces deux inductions séparémment
devient
m somme des
2 couples moyen que produiraient ces deux inductions séparémment
devient  voisine de
voisine de
 M, il est soumis de la part du
champ qui tourne dans le même sens à un couple moteur élevé,
le second champ (
M, il est soumis de la part du
champ qui tourne dans le même sens à un couple moteur élevé,
le second champ ( < 0) exerce lui un couple
résistant très faible que l'on va pouvoir négliger. Or
ces deux inductions peuvent être considérées comme la décomposition
d'une induction alternative de direction B0 : c'est le principe des
moteurs asynchrones monophasés qui sont
susceptibles de fournir du travail à condition qu'on les ait fait démarrer
par un artifice convenable (car à
< 0) exerce lui un couple
résistant très faible que l'on va pouvoir négliger. Or
ces deux inductions peuvent être considérées comme la décomposition
d'une induction alternative de direction B0 : c'est le principe des
moteurs asynchrones monophasés qui sont
susceptibles de fournir du travail à condition qu'on les ait fait démarrer
par un artifice convenable (car à  =
0 les deux couples sont égaux et opposés).
=
0 les deux couples sont égaux et opposés). |