Rappel du Principe
Par action
d'une induction tournante, obtenue par l'intermédiaire de courants polyphasés
dans les bobinage d'un stator, sur un circuit fermé on crée un
couple moteur de valeur moyenne non nulle susceptible d'entraîner le rotor
support de ce circuit.
Technologie du stator
Le stator
est conçu de la même façon pour un moteur asynchrone que
pour un moteur synchrone ou un alternateur polyphasé. On a vu que la
fréquence du courant définissait la vitesse angulaire, en fait
pour obtenir un fonctionnement plus satisfaisant mécaniquement, comme
pour les machines à courant continu on est amené à multiplier
le nommbre de pôles ce qui se traduit par une vitesse angulaire moindre.
Si l'on a 2p pôles la vitesse angulaire  s'obtient
à partir de la pulsation du courant par
s'obtient
à partir de la pulsation du courant par  = p
= p .
.
rotor
A p paires
de pôles fictifs correspondront p spires en court circuit de largeur égale
à l'intervalle polaire. Dans ces conditions, la force électromagnétique
d'entraînement F = Bli exercée sur chaque portion active de la
spire est maximale si la fem dans la spire e = BLv l'est (B induction, L inductance,
v vitesse angulaire du rotor) ce que l'on obtient évidemment si l'un
des brins de la spire se trouve en un point de B maximal (pôle nord) et
l'autre aussi (pôle sud) puisqu'alors les fem dans chaque brin actif sont
maximales et s'ajoutent donnant le maximum de courant et de couple.
Il y a cependant quelques inconvénients à ce montage simpliste
: d'une part, le rotor est mal utilisé (1 spire par 2 pôles), et
d'autre part, le couple moteur est pulsatoire à fréquence double
du courant dans les spires, ce qui mécaniquement n'est pas souhaitable.
En effet si l'on néglige l'inductance de chaque spire devant sa résistance,
BLv est en phase avec le courant i dans chaque brin actif, B et i passent ensemble
par un maximum (avec le même signe), il en résulte que le couple
 proportionnel à Bi varie sinusoïdalement
à fréquence double.
proportionnel à Bi varie sinusoïdalement
à fréquence double.

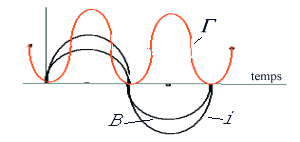
Ce problème est évité en garnissant l'armature du rotor
de nombreuses spires identiques et régulièrement décalées
les unes par rapport aux autres. Les couples s'ajoutent et, comme la somme de
fonctions sinusoïdales décalées, le couple résultant
est alors pratiquement une constante.
En pratique
cet enroulement est réalisé en "cage
d'écureuil" c'est à dire par un ensemble de barres
de cuivre, aluminium ou laiton disposées à la périphérie
du rotor et reliées entre elles par un anneau de forte section. Ce système
se justifie relativement aisément :

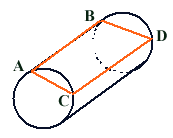
Soit une spire ABCD, si on néglige son inductance on a 2e = 2ri (avec
e dans chaque brin de résistance r) sur un brin actif la loi d'Ohm s'écrit
ri = VA - VB + e d'ou VA = VB ce
qui traduit le fait que toute l'énergie électrique induite est
consommée par effet Joule dans le brin AB, de même VC =
VD. Il en serait de même pour un autre brin. Il ne se passerait
donc rien si on connectait A et A' d'une autre spire voisine, d'où le
principe de la cage d'écureuil.
inductance des spires
Nous avons
jusqu'ici négligé l'inductance des spires, or Lw
n'est pas nul et en particulier au démarrage cela contribue à
affaiblir le couple (car i n'est plus en phase avec B) et à la limite
à empêcher le démarrage (le couple n'étant alors
pas constamment moteur).

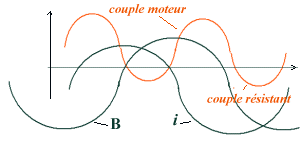
Pour limiter cet inconvénient il convient de réduire ce déphasage
donné par tg = L
= L /R.
Comme on ne peut modifier L on joue sur R en faisant une spire ouverte en série
avec un rhéostat de démarrage, connecté par l'intermédiaire
de bagues solidaires de l'axe du rotor et sur lesquelles frottent des balais
fixes solidaires du stator. Notons que ces balais sont en graphite et s'usent
par frottement au cours du fonctionnement, il conviendra donc de les changer
régulièrement.
/R.
Comme on ne peut modifier L on joue sur R en faisant une spire ouverte en série
avec un rhéostat de démarrage, connecté par l'intermédiaire
de bagues solidaires de l'axe du rotor et sur lesquelles frottent des balais
fixes solidaires du stator. Notons que ces balais sont en graphite et s'usent
par frottement au cours du fonctionnement, il conviendra donc de les changer
régulièrement.
Caractéristiques du moteur asynchrone
Appelons  0
la vitesse synchrone du moteur,
0
la vitesse synchrone du moteur,  1 sa
vitesse de rotation, r la résistance de l'enroulement rotor. Par rapport
au flux cet enroulement tourne à la vitesse relative
1 sa
vitesse de rotation, r la résistance de l'enroulement rotor. Par rapport
au flux cet enroulement tourne à la vitesse relative  0-
0- 1.
Soit Ct le couple transmis. Le bilan énergétique s'écrit
1.
Soit Ct le couple transmis. Le bilan énergétique s'écrit
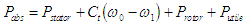 ce qui exprime
qu'aux pertes près le stator transmet au rotor la puissance Ct
ce qui exprime
qu'aux pertes près le stator transmet au rotor la puissance Ct  0
qui se divise en deux parts : l'effet Joule rotor et Ct
0
qui se divise en deux parts : l'effet Joule rotor et Ct 1 la puissance mécanique sur l'arbre.
1 la puissance mécanique sur l'arbre.
Le glissement s'exprime
par 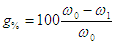
pertes Joules rotor
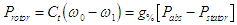
En gros 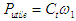 et
et 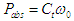 d'où
d'où
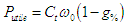 et le rendement
s'exprime alors par
et le rendement
s'exprime alors par 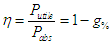
La conséquence c'est qu'il faut faire en sorte que le glissement soit
faible si on veut un rendement correct. On en déduit par ailleurs qu'à
couple constant la puissance absorbée est indépendante du glissement.
Enfin les pertes Joules évoluent avec le glissement, elles sont donc
maxi au démarrage (g = 1) et tendent vers zéro lorsqu'il y a synchronisme
(g = 0).
On a déjà
vu que le couple était maximal pour  =
=  M
tel que
M
tel que 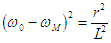 . Le même
raisonnement permet de montrer que cela correspond à L
. Le même
raisonnement permet de montrer que cela correspond à L = r et par ailleurs
= r et par ailleurs  M est indépendant
de r puisque
M est indépendant
de r puisque 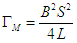 . On
peut montrer aussi qu'à glissement égal le couple est sensiblement
proportionnel au carré de la tension d'alimentation, tandis qu'à
couple égal le glissement est sensiblement proportionnel à la
résistance du rotor.
. On
peut montrer aussi qu'à glissement égal le couple est sensiblement
proportionnel au carré de la tension d'alimentation, tandis qu'à
couple égal le glissement est sensiblement proportionnel à la
résistance du rotor.
relations pratiques
On va faire
intervenir des paramètres relatifs. Posons 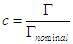 et
et 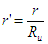 où
r est la résistance du rotor et Ru la résistance rotor
capable de donner le couple
où
r est la résistance du rotor et Ru la résistance rotor
capable de donner le couple  M au décollage
(quand g = 1)
M au décollage
(quand g = 1)

 ...
...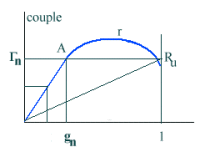
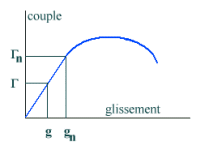
La caractéristique
de couple étant sensiblement une droite passant par g = 0, si gn
est le glissement normal on peut écrire avec ces notations 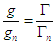 tandis que la relation entre g et r conduit à
tandis que la relation entre g et r conduit à 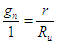 d'où l'on déduit aisément g = r'c relation pratique qui
implique la connaissance de Ru. On l'obtient en exprimant les pertes
Joule au décollage, ainsi pour un rotor triphasé
d'où l'on déduit aisément g = r'c relation pratique qui
implique la connaissance de Ru. On l'obtient en exprimant les pertes
Joule au décollage, ainsi pour un rotor triphasé 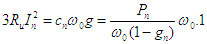 (car dans ce cas g = 1) d'où l'on tire Ru
(car dans ce cas g = 1) d'où l'on tire Ru 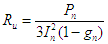 Pn et gn sont connues (valeurs nominales inscrites sur
la plaque constructeur) il reste donc à définir In
(courant rotor en marche normale). On sait que
Pn et gn sont connues (valeurs nominales inscrites sur
la plaque constructeur) il reste donc à définir In
(courant rotor en marche normale). On sait que 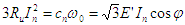 où E' est la fem du rotor au décollage. Au décollage la
résistance du rotor Ru est importante ce qui revient à
dire que le déphasage entre E' et In est minimal et cos
où E' est la fem du rotor au décollage. Au décollage la
résistance du rotor Ru est importante ce qui revient à
dire que le déphasage entre E' et In est minimal et cos = 1, les fuites sont relativement importantes ce qui revient à dire que
E' qui correspond au rotor en court-circuit est moindre que E correspondant
au rotor ouvert. On admet en pratique E'cos
= 1, les fuites sont relativement importantes ce qui revient à dire que
E' qui correspond au rotor en court-circuit est moindre que E correspondant
au rotor ouvert. On admet en pratique E'cos = 0.9E
= 0.9E
d'où les
relations approximatives mais suffisantes 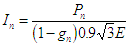 et
et 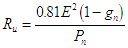




 s'obtient
à partir de la pulsation du courant par
s'obtient
à partir de la pulsation du courant par  = p
= p .
. proportionnel à Bi varie sinusoïdalement
à fréquence double.
proportionnel à Bi varie sinusoïdalement
à fréquence double.





 = L
= L /R.
Comme on ne peut modifier L on joue sur R en faisant une spire ouverte en série
avec un rhéostat de démarrage, connecté par l'intermédiaire
de bagues solidaires de l'axe du rotor et sur lesquelles frottent des balais
fixes solidaires du stator. Notons que ces balais sont en graphite et s'usent
par frottement au cours du fonctionnement, il conviendra donc de les changer
régulièrement.
/R.
Comme on ne peut modifier L on joue sur R en faisant une spire ouverte en série
avec un rhéostat de démarrage, connecté par l'intermédiaire
de bagues solidaires de l'axe du rotor et sur lesquelles frottent des balais
fixes solidaires du stator. Notons que ces balais sont en graphite et s'usent
par frottement au cours du fonctionnement, il conviendra donc de les changer
régulièrement. 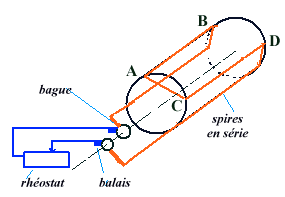
 0
la vitesse synchrone du moteur,
0
la vitesse synchrone du moteur,  1 sa
vitesse de rotation, r la résistance de l'enroulement rotor. Par rapport
au flux cet enroulement tourne à la vitesse relative
1 sa
vitesse de rotation, r la résistance de l'enroulement rotor. Par rapport
au flux cet enroulement tourne à la vitesse relative  0-
0- 1.
Soit Ct le couple transmis. Le bilan énergétique s'écrit
1.
Soit Ct le couple transmis. Le bilan énergétique s'écrit
 0
qui se divise en deux parts : l'effet Joule rotor et Ct
0
qui se divise en deux parts : l'effet Joule rotor et Ct 1 la puissance mécanique sur l'arbre.
1 la puissance mécanique sur l'arbre. =
=  M
tel que
M
tel que  = r et par ailleurs
= r et par ailleurs  M est indépendant
de r puisque
M est indépendant
de r puisque  M au décollage
(quand g = 1)
M au décollage
(quand g = 1)
 ...
...
 = 1, les fuites sont relativement importantes ce qui revient à dire que
E' qui correspond au rotor en court-circuit est moindre que E correspondant
au rotor ouvert. On admet en pratique E'cos
= 1, les fuites sont relativement importantes ce qui revient à dire que
E' qui correspond au rotor en court-circuit est moindre que E correspondant
au rotor ouvert. On admet en pratique E'cos = 0.9E
= 0.9E![]() et
et ![]()
