systèmes
de numération
Avant
d'introduire les notions de codage et décodage nous rappelons le
principe des systèmes de numération et les procédures
pour passer d'une base dans une autre.
427 en système
décimal c'est égal à 4.102 + 2.101
+ 7.100,
c'est à dire que dans un système de base donnée un nombre
s'écrit
N(B)
= anBn + an-1Bn-1 + ...+ a1B1
+ a0B0
avec les coeficients
an entiers et compris entre 0 et B-1. Et on écrira le nombre
an....a1a0
système
binaire
En base 2
on aura environ 3 fois plus de chiffres qu'en base 10 pour exprimer la même
quantité.
Par ex : 99
(en base 10) = 64 + 32 + 2 +1 soit 26 + 25 +0.24
+ 0.23 + 0.22 + 21 +20 = 1100011
en base deux
Un nombre
fractionnaire va s'exprimer par N = an2n +...+ a020
+ a-12-1 + a-22-2 +...+a-n2-n
par ex 27.25
= 16 + 8 + 2 + 1 + (1/4) or 1/4 = 1.2-2 d'où 11011,01
Remarque
pratique : déplacer une virgule d'un cran vers la droite revient
à multiplier le nombre par la base, et inversement la déplacer
vers la gauche correspond à une division par la base. Cela sera évidemment
exploité dans les composants numériques.
Transcodage
C'est le processus
de passage d'une base dans une autre
ex: 1227(10)
= 2313(8) La procédure consiste à diviser le nombre
décimal par 8, le reste de la division donne le coefficient a0,
et on recommence jusqu'à obtenir un résultat inférieur
(ou au plus égal) à B-1.
Pour la détermination
de la partie fractionnaire, quand il y en a une, on procède de manière
symétrique, on multiplie par la base, la partie entière donne
le premier coefficient, et on recommence jusqu'à épuisement.
Ainsi 0.25 en base deux va donner .25x2 =0.5 soit partie entière 0 donc
le coefficient a-1 = 0, ensuite 0.5x2=1 donc le coefficient a-2
vaut 1 et le reste fractionnaire est maintenant nul. Donc la conversion est
terminée et le résultat est donc 0,01.
système
BCD (décimal codé binaire)
Il s'agit
du système employé dans les calculatrices de bureau par exemple,
et exploité par nombre d'afficheurs, chaque chiffre d'un nombre décimal
va être codé séparément en binaire ce qui donne par
exemple
| 328(10) = |
0011 |
0010 |
1000 |
| |
3 |
2 |
8 |
Passage
binaire/décimal/octal/hexadécimal
| 357(10)équivaut à |
000101100101 en binaire |
| soit 545(8) |
101 |
100 |
101 |
| |
5 |
4 |
5 |
| ou 165(16) |
0001 |
0110 |
0101 |
| |
1 |
6 |
5 |
On voit
aisément la méthode pour passer en octal
à partir du binaire
il suffit de grouper les chiffres binaires par groupes de 3 (à partir
de la droite) et de transcrire, ce qui est immédiat, les nombres obtenus
en leur équivalent décimal. La méthode est semblable
pour l'hexadécimal mais en regroupant
par paquets de 4 chiffres.
La conséquence
de cette remarque est immédiate, lorsqu'on va manipuler des nombres
binaires importants on préférera, pour éviter les erreurs
de transcription, manipuler leurs équivalents hexadécimaux :
il est clair qu'il est plus sûr d'écrire 165 que 000101100101.
Rappelons enfin qu'en hexadécimal les symboles pour représenter
les nombres de 10 à 15 sont les 6 premières lettres de l'alphabet
A correspond à 10, etc, jusqu'à F qui équivaut au nombre
décimal 15.
système
combinatoire universel
Quelques définitions. On appelle minterme de 2 variables a et b un monôme
de type ab, ab, ab
ou ab.(avec l'habituelle convention typographique
d'écrire en rouge les variables surlignées). Pour 2 variables
on aura 22 mintermes et 2n pour n variables.
Un démultiplexeur
sera un système qui réalise les 2n mintermes de n
variables.
Remarque : toute fonction logique est la somme de plusieurs mintermes (ou
constituée d'un seul parfois), ce qu'on a appelé la forme canonique
de la fonction.
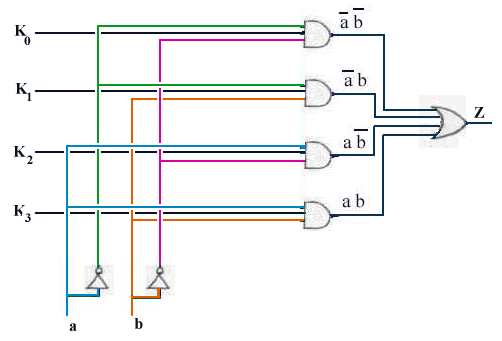
Un système combinatoire universel, ou multiplexeur à n variables
[data selector en anglais] est un système qui réalise
la fonction universelle de n variables. Par exemple, dans le cas de deux variables
a et b, cette fonction s'exprime selon l'équation ci-dessous :
Z[a, b;
K0 K1 K2 K3] = K0.a.b + K1.a.b
+ K2.a.b + K3.a.b
A partir
du démultiplexeur précédent on peut imaginer un tel système
dans lequel K0, K1, K2, K3 sont des variables auxiliaires, ou plutôt
des paramètres (valant 0 ou 1 évidemment).
Pour obtenir par exemple Z = a.b + a.b il
suffit de faire K0 = K3 = 1, K1 = K2 = 0
codeurs
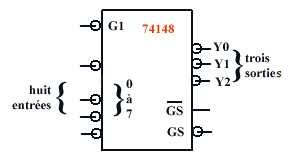
On peut
donc réaliser des circuits dits de codage comportant 2n
entrées et n sorties binaires. Ainsi par exemple le 74148 possède
8 entrées d'information décimale qu'il va coder en binaire
Si G1 est
au niveau haut les entrées n'ont aucun effet, toutes les sorties sont
au niveau haut (y compris GS et GS)
Si G1 est bas et que toutes les entrées sont à 1 alors toutes
les sorties sont à 1 sauf GS
Ensuite le fonctionnement est le suivant : pour G1 = 0 sera prise en compte
l'entrée au niveau bas de rang le plus élevé, ainsi soit
la configuration suivante :
| G1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Y2 |
Y1 |
Y0 |
GS |
GS |
| 0 |
X |
X |
X |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
Le niveau
0 en 3 donne les sorties Y0 et Y1 actives (niveau bas) quelles que soient
les valeurs des entrées 0, 1 et 2.
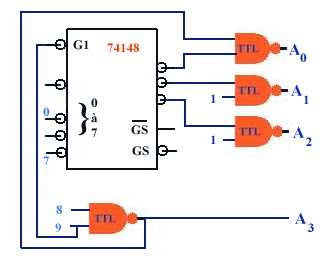
Pour avoir
une correspondance binaire traditionnel (donc 011 correspondant à3)
il suffit de rajouter un NAND sur chaque sortie. On peut ainsi aisément
faire un codeur BCD (entrées actives au niveau bas mais sorties au
niveau haut)
Notons que
le 74147 est directement un codeur décimal-BCD mais dont les entrées
et sorties sont actives au niveau bas et qui ne possède pas d'entrée
de validation G1.
décodeur
: n entrées 2n sorties
Pour chaque
combinaison d'entrée une seule sortie est validée. Notons qu'il
existe des décodeurs possédant une borne G1 de validation d'entrée,
certains fournissent en sortie à la fois le niveau haut et bas (sur
2 séries de bornes).
Les décodeurs
sont utilisés :
-
pour
le décodage d'adresse
- pour la commande d'afficheurs
- comme générateurs
de fonctions
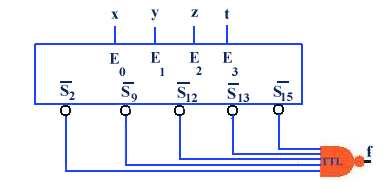
Par exemple,
soit la fonction f = xyzt + xyzt
+ xyzt + xyzt
+ xyzt, chacun des termes de la fonction
peut être obtenu avec un décodeur où
| x = 20 |
soit xyzt = 15 |
| y = 21 |
xyzt
= 12 |
| z = 22 |
etc.. |
| t = 23 |
|
d'où
le câblage avec un décodeur par 16
Notons l'existence
d'un décodeur BCD-décimal (4 entrées et seulement 10 sorties)
: le circuit 7442 (sortie active niveau bas, entrée niveau haut)
transcodeur
Une application particulière des décodeurs est l'affichage très
classique à 7 segments. Il s'agit de passer du BCD au mode 7 segments
dont le schéma de principe est le suivant. Ici on prendra l'exemple du
circuit TIL 302 dans lequel l'allumage d'un segment (diode électroluminescente)
est obtenu en reliant la cathode correspondante au zéro.
Soit la table
de vérité dans laquelle on ne s'intéresse qu'aux dix chiffres
habituels. Parconvention on dira a=1 si a est allumé.
| chiffre |
U3 |
U2 |
U1 |
U0 |
|
a |
b |
c |
d |
e |
f |
g |
| 0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
| 1 |
|
|
|
1 |
|
|
1 |
1 |
|
|
|
|
| 2 |
|
|
1 |
|
|
1 |
1 |
|
1 |
1 |
|
1 |
| 3 |
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
1 |
| 4 |
|
1 |
|
|
|
|
1 |
1 |
|
|
1 |
1 |
| 5 |
|
1 |
|
1 |
|
1 |
|
1 |
1 |
|
1 |
1 |
| 6 |
|
1 |
1 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
| 7 |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
|
|
|
|
| 8 |
1 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 9 |
1 |
|
|
1 |
|
1 |
1 |
1 |
|
|
1 |
1 |
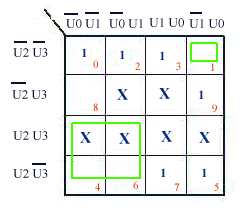
On va exploiter
le diagramme de Karnaugh pour expliciter les fonctions associées à
chacune des électrodes. Prenons a pour commencer
Sur ce diagramme
on a figuré en rouge le chiffre correspondant à chaque case,
ainsi la case 4 en bas à gauche correspond bien à U0U1U2U3
comme l'indique la ligne 4 de la table de vérité. Les cases
comportant un X sont celles correspondant au décodage des chiffres
supérieurs à 9 qui ne nous intéressent pas ici. Ces cases
seront donc indifféremment mises à 1 ou 0 selon le besoin de
simplification. Les cases à 1 correspondent aux 1 de la colonne a dans
la table de vérité.
La remarque importante est qu'une diode sera allumée si l'on met sa cathode
à zéro. Ce sont donc les états 0, et non 1 comme habituellement,
qui vont nous intéresser ici et on va calculer non pas a mais a.
Sur le tableau de Karnaugh ci-dessus on voit donc que l'on dispose d'un 0 en
haut isolé ce qui nous donne donc U0U1U2U3
et en bas à gauche on a deux 0 juxtaposés avec deux cases
indifférentes ce qui conduit à une simplification par U1U3 il
reste donc U2U0.
On
adoptera la même démarche pour l'ensemble des autres électrodes
et au final on aboutit à la série d'équations suivante
:
a
= U0U1U2U3 + U0U2
b = U0U1U2
+ U0U1U2
c
= U0U1U2
d
= U0U1U2 + U0U1U2
+ U0U1U2
e
= U0 + U1U2
f
= U0U1 + U1U2 + U0U2U3
g
= U1U2U3 + U0U1U2
D'où
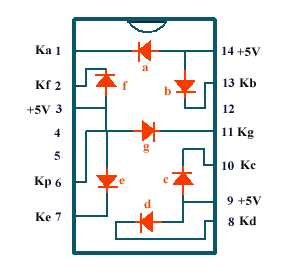
le schéma du décodeur dont le type est le 7447 qui comporte
en outre 3 entrées de validation et de test dont la combinaison permet
soit un affichage normal, soit l'extinction de tous les segments, soit leur
allumage (test)
Comparateur
C'est
un circuit lui aussi fréquemment employé et dont la fonction
est de comparer 2 nombres binaires. Nous donnons ici le principe dans le
cas de comparaison de deux nombres a et b d'un seul bit.
| a |
b |
a > b |
a = b |
a < b |
| 0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
| |
|
f = a b |
f = a ou exclusif b |
f = a
b |
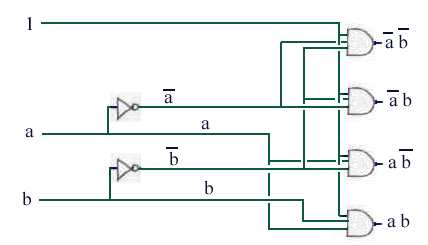
D'où
on tire le logigramme qui est très simple.
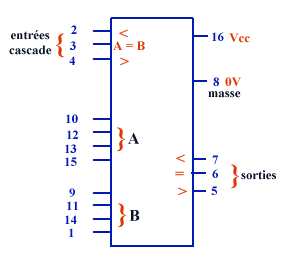
Il existe
un circuit intégré permettant la comparaison non de bits mais
directement de mots de 4 bits. Lorsqu'on voudra comparer des mots de plus
de 4 bits on placera deux comparateurs en cascade en reliant les sorties
du premier aux entrées du second sur lequel on entrera les poids
fort des mots A et B.
