
Copyright
© 2000-2015
LHERBAUDIERE
6 pages à l'impression
version
initiale 2002
dernière
mise à jour
22 mars 2013
22 mars 2013
 |
Copyright |
6 pages à l'impression |
version
initiale 2002 |
||
| dernière
mise à jour 22 mars 2013 |
première partie (1/6) : déformations élastiques des solides
| module
d'Young et Poisson |
||||
| une
poutre encastrée, soutenue |
||||
| le
ressort de réveil |
||||
| le
module de glissement |
||||
| une collection d'icônes pour visiter tout le site | ||||
- les déformations sont proportionnelles aux contraintes et réversibles
- les déformations sont parfaitement élastiques
- la relation de correspondance est linéaire : loi de Hooke.

 l
/ l = F/S
l
/ l = F/S 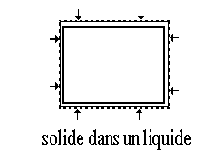
 V/V
= F/ SK et l'on définit un coefficient de compressibilité
= 1/K
V/V
= F/ SK et l'on définit un coefficient de compressibilité
= 1/K
 tel que
tel que  R
/ R = -
R
/ R = - 
 l
/ l
l
/ lb) limite d'élasticité

| acier | cuivre | alu | |
| L hbar | 40 | 3 | 10 |
| R | 80 | 25 | 12 |
| dl/l rupt | 0.2 | 0.4 | 0.3 |

poutre encastréeOn néglige le poids de la poutre devant la force F.

 = df / x soit df
= x dx/r , f étant la flèche totale de l'extrêmité
de la poutre et df la variation de flèche de P à Q
= df / x soit df
= x dx/r , f étant la flèche totale de l'extrêmité
de la poutre et df la variation de flèche de P à Q /dx = y/r.
Cette fibre est en équilibre sous l'action du moment de la force F appliquée
en P soit - Fx et du moment de la force de traction exercée par la partie
gauche de la poutre dans l'axe de la fibre telle que dF= dS E y/r, dS étant
la section calculée à partir de la fibre neutre. soit d
/dx = y/r.
Cette fibre est en équilibre sous l'action du moment de la force F appliquée
en P soit - Fx et du moment de la force de traction exercée par la partie
gauche de la poutre dans l'axe de la fibre telle que dF= dS E y/r, dS étant
la section calculée à partir de la fibre neutre. soit d (perpendiculaire
à p).
(perpendiculaire
à p). = S dF y = E/r SdSy2 et en
posant j = SdSy2 = moment d'inertie de la section droite par
rapport à l'axe passant par P et perpendiculaire à OP, on
obtient
= S dF y = E/r SdSy2 et en
posant j = SdSy2 = moment d'inertie de la section droite par
rapport à l'axe passant par P et perpendiculaire à OP, on
obtient  = E/r j soit encore
= E/r j soit encore  = df Ej / xdx puisque df = x dx/r à l'équilibre
df Ej / xdx = Fx et en intégrant de A à B
= df Ej / xdx puisque df = x dx/r à l'équilibre
df Ej / xdx = Fx et en intégrant de A à B  / Ej=
Fx / Ej est nulle en B (x = 0) et maximale en A et n'est donc
pas constante.
/ Ej=
Fx / Ej est nulle en B (x = 0) et maximale en A et n'est donc
pas constante.poutre soutenue

df Ej / xdx=Fx/2 ..............pour une même longueur de poutre, à F identique la flèche est donc 16 fois moindre que pour une poutre encastrée.
application au cas d'une poutre homogènerectangulaire d'épaisseur e, de largeur b et de longueur l


 =
=  dl / Ej et pour le ressort de longueur
l on obtient
dl / Ej et pour le ressort de longueur
l on obtient  =
=  l
/ Ej ce qui revient à dire que si l'on applique un moment de force
l
/ Ej ce qui revient à dire que si l'on applique un moment de force  le ressort tourne de
le ressort tourne de  .
.  /
/ = Ebe3 / 12l .
= Ebe3 / 12l .action d'un couple longitudinalmodule de rigidité ou de glissement G

 (RADIANS) d'un élément cubique de section S dont la base est supposée
fixe s'exprime par F = GS
(RADIANS) d'un élément cubique de section S dont la base est supposée
fixe s'exprime par F = GS dans laquelle G est le module de rigidité pour le fer G = 8000 hbars
dans laquelle G est le module de rigidité pour le fer G = 8000 hbars
torsion d'un cylindre (fil cylindrique de rayon r)

 dS = d(
dS = d( r2) = 2
r2) = 2 rdr
rdr G
G /l
d'où dG = 2
/l
d'où dG = 2 G
G
 /l r3dr
/l r3dr d4G
d4G /32l
/32l |