Copyright
© 2000-2015 LHERBAUDIERE


7 pages à l'impression
version initiale 2002
dernière mise à jour
22 mars 2013

cliquez sur le mot avertissement ou information ci-dessus pour connaitre une info essentielle avant de lire ce module et n'hésitez pas à cliquer en bas de page sur l'icone sommaire du site ça vous ouvrira d'autres perspectives

Mesure des Champs Magnétiques

première partie (1/5) : l'effet Hall

les divers principes
un phénomène très simple
une conséquence
les plus adaptés
les deux options
une collection d'icônes pour visiter tout le site

introduction

Les méthodes de mesure des champs magnétiques sont assez nombreuses et il existe plusieurs principes de capteurs magnétiques, allant du plus complexe, souvent réservé aux laboratoires ou à des applications très spécifiques, au plus simple, d’emploi courant en milieu industriel ou grand public:
  • élément Hall
  • élément à effet magnétorésistif
  • élément à effet Wiegand
  • transistor magnétique
  • SQUID
  • fluxgates
  • capteurs magnétiques à fibres optiques
  • capteurs à résonance magnétique nucléaire
En fait on peut considérer qu'il existe deux classes de dispositifs de mesure de champ magnétique, ceux pour les champs forts (gaussmètres) et ceux pour les champs faibles (magnétomètres)


Nous ne nous intéresserons, ici, qu'aux capteurs d'utilisation courante et ayant un principe de base relativement simple. Les deux premiers types, sonde à effet Hall et magnétorésistance, sont les plus utilisés dans le secteur industriel (champs forts) tandis que les fluxgates et SQUIDs sont la base des magnétomètres les plus performants.


On appelle champ magnétique l'une des formes de manifestation du champ électromagnétique. La particularité de ce champ est qu'il n'agit que sur les particules et corps chargés électriquement en mouvement, ainsi que sur les corps aimantés indépendamment de leur mouvement. Le champ magnétique est créé par les conducteurs parcourus par un courant, par les particules et corps chargés électriquement en mouvement, par les corps aimantés ainsi que par tout champ électrique variable.

Le vecteur induction magnétique B est la caractéristique de force d'un champ magnétique Il est numériquement égal à la limite du rapport de la force, agissant de la part du champ magnétique sur l'élément de conducteur parcouru par un courant électrique, au produit du courant par la longueur de l'élément de conducteur, lorsque la longueur de cet élément tend vers zéro et que l'élément est disposé dans le champ de telle sorte que cette limite admette sa valeur maximale.


Rappelons que sous l’effet d’un champ magnétique la matière s’aimante, c’est à dire que chaque élément de volume dv est le siège d’un moment magnétique M et on définit l’intensité d’aimantation J =dM/dv et on obtient ainsi une relation entre l’induction magnétique B et le champ H qui s’exprime par B=µ0(H+J).

µ0 est la perméabilité magnétique du vide qui dans le système d'unités international vaut 410-7 H/m.

L’expérience montre que pour certaines substances l’intensité d’aimantation est proportionnelle au champ magnétique ce qui entraîne alors B=µH où µ, la perméabilité magnétique relative de la substance, s’exprime alors selon la relation :

µ=µ0(1+) où représente la susceptibilité magnétique.

On distingue
  • les corps paramagnétiques dont la susceptibilité est positive mais de l’ordre de 10-2,
  • les diamagnétiques où elle est négative et de l’ordre de 10-5
  • et enfin les ferromagnétiques, où le rapport entre l’intensité d’aimantation et le champ magnétique peut être très grand.
Dans tous les cas le phénomène est lié au fait qu’un électron soumis à un champ magnétique va subir une perturbation, c’est à dire qu’il va prendre un moment magnétique. Si l’on considère un électron dans un solide, on peut considérer qu’il circule sur une trajectoire circulaire de rayon r avec une vitesse angulaire.

Le courant équivalent à cet électron est i = - e/2 et en appliquant la loi de Laplace on voit que le moment magnétique est tandis que le moment cinétique du même électron est =mr2.

A cela on doit ajouter un terme dû au spin de l’électron (c’est à dire à sa rotation sur lui-même dans un sens ou l’autre) qui s’exprime par ±he/4m, avec h constante de Planck.

Les différents types de comportement magnétique s’expliquent par le type d’organisation de la matière. Selon le matériau l’organisation structurelle va induire une compensation plus ou moins importante des moments magnétiques des divers électrons ou au contraire une addition de ceux-ci.

Ainsi si les matériaux ferro et ferrimagnétiques seront les constituants privilégiés des aimants permanents, il paraît évident que les semi-conducteurs, avec leur nombre réduit de porteurs, auront vraisemblablement une certaine sensibilité au champ magnétique et seront les vecteurs privilégiés de sa mesure.

L’effet Hall



Cet effet a été découvert par Edwin Herbert Hall en 1879, sur des feuilles métalliques, Hall observa sur des bandes de cuivre parcourues par un courant l'apparition d'une différence de potentiel lorsqu'un champ magnétique était appliqué à ces bandes. Si un ruban conducteur est parcouru par un courant électrique et si un champ d’induction magnétique est perpendiculaire au plan du ruban il apparaît une ddp entre les bords du ruban.

Théorie élémentaire


Jusqu'aux années 1960, l'effet Hall a été principalement utilisé pour analyser la nature des porteurs de charge présents dans un solide, leur concentration et leur mouvement. Ultérieurement, l'introduction de composants à matériaux semi-conducteurs, comme l'antimoniure d'indium et l'arseniure d'indium, a permis l'obtention de tensions de Hall suffisamment élevées pour justifier son emploi dans l'industrie.

Les principales applications concernent les gaussmètres, les ampèremètres, les wattmètres, les moteurs à courant continu, les multimètres analogiques, les compas magnétiques et nombre d'instruments et dispositifs exploitant la mesure de l'intensité et/ou la direction d'un champ magnétique ou d'un courant dans un conducteur.

L’effet Hall est un phénomène général, cependant c’est dans les semi-conduteurs que son amplitude est la plus marquée. Considérons un cristal semi-conducteur homogène de type p (figure de droite) de forme parallélépipédique orienté selon le système d’axe trirectangle classique, traversé par un courant de trous selon Oy, d’intensité i provoquant un champ interne Ey et plongé dans un champ magnétique d’induction Bz orienté selon Oz.


Selon la théorie élémentaire de la conductivité les trous acquièrent une vitesse moyenne d’entraînement parallèle à Ey de valeur vdp=µpEy. Ces charges subissent du fait du champ magnétique une force F= -qvdpB (force dite de Lorentz, ou de Laplace, dirigée vers la gauche). Il en résulte une tendance à l’accumulation de charges positives sur la face gauche et, symétriquement, un défaut de telles charges sur la face droite, ce qui se traduit par un champ électrique transversal EH, et, puisque le champ dérive d’un potentiel, une ddp

VH est dite tension de Hall

Puisqu’aucun courant n’est débité entre les bornes A et B, cela revient à dire que la force qEH due à EH est équilibrée par la force de Laplace -qvB on en déduit aisément que la tension de Hall s’exprime par :

VH = lxµpEyB et si lx, ly , lz sont les dimensions du barreau, et p la concentration en trous : sachant que la densité de courant est proportionnelle à qpvdp, le courant i en intégrant sur l'ensemble de la section s'exprime par

i = qpvdplxlz, il vient donc VH = (1/qp)(i/lz)B, on appelle la quantité Rp = 1/qp constante de Hall pour les trous.

Si le courant était du à des électrons (figure de gauche) le résultat serait semblable à condition de changer q en -q et p en n.

Il en résulte que la tension de Hall est :
- proportionnelle à l’intensité du courant i et à l’induction magnétique B

- et inversement proportionnelle à l'épaisseur lz du barreau et à la concentration en porteurs n ou p.
Mais ainsi que le montre le graphique ci-après (dans le cas du silicium et pour deux concentrations différentes de dopant) la température est un élément ayant une grande influence sur la mobilité, ce qui sera le plus souvent un inconvénient. Il faudra donc choisir le matériau le moins sensible à la température dès lors qu’on souhaitera un capteur utilisable sur un intervalle étendu de température.


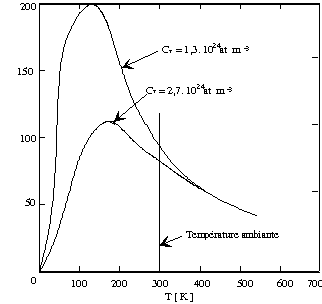
Fig. influence de la température sur la mobilité

Eléments magnéto-résistifs


En exploitant dans un semi-conducteur, soumis à un champ magnétique, la variation de résistivité du matériau résultant de la distorsion des trajectoires électroniques on peut réaliser des éléments dits magnéto-résistifs.

Ils sont constitués d'une résistance dont la valeur dépend de l'induction magnétique dans laquelle elle est placée. Une forme de disque à électrodes circulaires coaxiales pour l'élément magnétorésistif est idéale du point de vue de la sensibilité, mais la résistance de l'élément est faible, et sa mise en oeuvre est difficile. Il existe également une forme en plaque lustrée, composée de courtes bandes, accolées sur un semi-conducteur fin et long, et perpendiculaires à sa longueur. Il s'agit d'une constitution qui relie en série de nombreux éléments magnétorésistifs, et, en utilisant un grand nombre d'éléments, on peut augmenter la valeur de la résistance de l'ensemble.

Les éléments magnétorésistifs à semi-conducteur sont largement utilisés dans les dispositifs à résistance variable sans contact, potentiomètres, magnétomètres, ampèremètres, amplificateurs d'oscillations et de déplacements, multiplicateurs, calculateurs analogiques, wattmètres de micro-ondes, détecteurs de rotation, dispositifs de reconnaissance de billets de banque, etc.

Capteurs à effet Hall et magnétorésistifs

matériaux utilisables


Afin d’obtenir une grande sensibilité on utilisera les matériaux ayant la plus grande valeur de mobilité. Le tableau ci-dessous rappelle les caractéristiques électriques des principaux matériaux semi-conducteurs envisageables.

AlSb InP InAs InSb GaAs GaSb
m n (cm2/Vs) 4600 33000 78000 8500 4000
mp (cm2/Vs) 420 150 460 750 400 1400
Eg .(eV) 1,6 1,26 0,35 0,167 1,35 0,67
ni . (cm-3) 2. 1016 107

rappel : 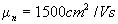pour le silicium

Parmi les matériaux semi-conducteurs l’antimoniure d’indium InSb semble le plus intéressant. Sa résistivité est de et son coefficient de Hall de

D’autres matériaux ont été également développés, en particulier dans les laboratoires de Siemens-Schukert où a été élaboré un eutectique InSb-NiSb. Il s’agit d’un antimoniure d’indium avec des inclusions orientées conduisant bien l’électricité. Il permet la réalisation de plaquettes de très faibles dimensions et présentant une résistance Ro d’environ 10 à 500.

Les zones de conduction métallique dans ce matériau sont distantes de quelques millièmes à quelques dix millièmes de millimètre. Lorsqu’une tension est appliquée à la plaquette, les lignes de courant sont orientées comme s’il n’y avait pas d’inclusion à conduction métallique.

L’application d’un champ magnétique perpendiculairement au plan de la plaquette fait toutefois dévier les lignes de courant par rapport à la direction initiale d’un angle d’environ 80° pour une induction magnétique d’un tesla, ce qui entraîne une augmentation considérable de la résistance pure dans le rapport de

ce rapport est théoriquement de l’ordre de 40.

L’augmentation de la résistance dans le champ magnétique est en fait égale à la moitié de la valeur théorique car la distance entre les zones à conduction métallique ne peut pas être réduite à volonté et la conductivité spécifique de l’antimoniure de nickel inclus n’est pas infinie.

La résistance à température ambiante augmente 10 fois pour une induction magnétique de 0,7 T et de 19 fois à 1 T.

Tableaux des caractéristiques thermodynamiques et chimiques essentielles des composés semi-conducteurs de type III-V et des éléments simples les constituants

Composé Paramètre de réseau
de type blende [nm]		 Chaleur de formation
[kj/mole]		 Energie du gap
[eV]		 Point de fusion
[K]
InSb 0,6478 -30,51 0,18 (d) 808
InAs 0,6058 -58,52 0,35 (d) 1216
InP 0,5868 -88,61 1,35 (d) 1343
GaSb 0,5642 -71,06 1,43 (d) 1511
GaP 0,5450 -100,32 2,26 (i) 1813

NB : (d) transition directe (i) transition indirecte

Eléments Potentiel d’oxydation Points de fusion [K] Pression de vapeur à 273K [Pa]
In 0,40 429 1,3´10-7
Ga 0,65 303 1,3´10-9
Al 1,67 932 1,3´10-9
Sb -0,21 903 1,3´10-1
As -2,25 se sublime 1,3´101

Les tableaux ci-dessus permettent de comprendre les problèmes de réalisation pratique d’éléments Hall. En effet InSb est le matériau le plus intéressant, mais comme le montre le second tableau l’antimoine présente une pression de vapeur environ un million de fois supérieure à celle de l’indium ce qui va poser de gros problèmes lors d’une coévaporation pour réaliser un capteur miniaturisé en couche mince de composition stoechiométrique correcte (voir complément dans le chapitre suivant : procédure d'obtention d'une couche d'InSb). Le problème est semblable avec l’AsGa.

C’est cependant la technologie couche mince qui conduit aux capteurs les plus performants ainsi qu’en témoignent les tableaux de caractéristiques fournis par les constructeurs (ci-après).

Caractéristiques comparées d’éléments Hall

Elément Hall en AsGa

    1. Gamme de température large (de 218 K à 398 K).
    2. Bonne précision pour des champs magnétiques élevés.
    3. Bonne caractéristique en fréquence.
    4. Faible coefficient de température de la tension de Hall ( environ -0,006%/ K).
    5. Tension de sortie faible.

Elément Hall en InSb

    1. Tension de sortie élevée (quelque dizaines de fois supérieure à l’élément Hall en AsGa).
    2. Prix moins élevé.
    3. Bonne caractéristique de température (quand on alimente en tension constante).
    4. Gamme de température : environ de 253 K à 373 K.
Les caractéristiques générales des capteurs basés sur l’effet Hall sont les suivantes :

longue durée de vie. rapidité de la réponse opération sans contact
compatible logique large gamme de température usure négligeable
bonne stabilité de fonctionnement.
Les tableaux ci-dessous, issus d’une compilation de données fournies par quelques constructeurs, donnent à titre d’exemple et sans présenter un caractère d’exhaustivité, un aperçu des caractéristiques de quelques capteurs à effet Hall et magnétorésistifs commercialisés en 2002.
Fabricant Référence Matériaux techno-
logie		 R
interne
[]		 Courant alim mA ou volt. Sensibilité
mV/mA.kG		 Coefficient de temp.
[%/ K]		 Tension
de Hall
[mV]
ASAHIKASE KH-400A SbIn dépôt c.m. 240-550 5 60 -0,8 300
PIONNEER LPH-012 SbIn dépôt c.m. 150-420 10 <70 -1 <700


DENKIONKYO


 5F-MS4-07F

20J-MP2-7F

20K-MP2-7F

10H-MP3-7F		 SbIn

SbIn

SbIn

SbIn		 massif

massif

massif

massif		 8-50

0.8-1.5K

9-3K

3--400K		 50

5(V)

3(V)

1(V)		 16,5
12

17

30		 -

-0,2

-0,2

-0,2		 825

60

50

100






SIEMENS



 SV200(III)

SBV566

SV110

FA218

FA22E

FA24		 SbIn

SbIn

SbIn

AsIn

AsIn

AsIn		 dépôt c.m.

massif

dépôt c.m.

massif

massif

massif		 40-80

30

500

3

2

1,4		 25

25

25

100

150

400		 1

3,2

10

0,085

0,08

0,075		 -0,1

-2,0

-1,0

-0,1

-0,1

-0,06		 25

80

250

8,5

12

30
NANA ELECT.
 
AG-1

AG-4		 Ge

Ge		 massif

massif		 40

300		 20

15		 0,4

2,9		 0,02

0,02		 8

43,5
COPAL TC8101 Ge massif >2 35 0,06 0,02 2,1
TOSHIBA

 THS-101

THS-102		 AsGa

AsGa		 épitaxiale

épitaxiale		 150-600

450-900		 5

5		 11,4

20		 -0,06 max

-0,06 max		 57

100
MATSUSHITA OH001 AsGa épitaxiale 0.5K-1.5K 6(V) 20 -0,06 max 112,5
VICTOR VHG-110 AsGa épitaxiale 200-800 5 12,5 -0,06 max 62,5

Tableau de caractéristiques de différents éléments à effet magnétorésistif

Fabricant Référence Matériaux température
d'utilisation [K]		 Résistance
[]		 Tension
d'alim [V]		 Tension de
sortie[mV]
MURATA LP-18S SbIn 263-333 2~10k 7 3,5
MURATA FPC-2R-04 SbIn 263-343 0,7~1,5k 8 0,5
MURATA FPC-4R-22 SbIn 263-353 0,2~1k 6,5 0,26
MURATA BS-H-V SbIn 253-343 0,5~5k 7 0,55
TOKYOSANYO MS-F SbIn 243-358 0,6~4,5k 5,5 0,15
NIHON AUTO. ME-01 233-353 7±2,5k 10
SIEMENS FP17D500E SbIn/SbNi 253-383 500
SIEMENS FP30L100E SbIn/SbNi 253-383 100
SIEMENS FP212L100-2 SbIn/SbNi 253-383 300 10
DENKIONKYO MR18SN SbIn 263-343 200 7
DENKIONKYO CMR10 SbIn 263-353 240 6