Dans
ce chapitre nous présenterons quelques méthodes permettant
la synthèse des circuits combinatoires. Ici encore il ne s'agit pas
d'examiner in extenso toutes les méthodes, mais de donner
un aperçu, pour le lecteur néophyte, en traitant quelques
exemples simples.
Circuit
combinatoire dont on donne la table de vérité
La première
étape consiste à déduire, à partir de cette table
de vérité, les équations logiques représentatives
du dispositif à concevoir. Ensuite on exprimera la forme canonique, puis
la forme simplifiée qui conduit au schéma électronique.
Soit l'exemple
d'une fonction de 3 variables ABC répondant à la table suivante:
| |
A |
B |
C |
F |
| |
0 |
0 |
0 |
0 |
| |
1 |
0 |
0 |
0 |
| f1 |
0 |
1 |
0 |
1 |
| |
1 |
1 |
0 |
0 |
| |
0 |
0 |
1 |
0 |
| |
1 |
0 |
1 |
0 |
| f2 |
0 |
1 |
1 |
1 |
| f3 |
1 |
1 |
1 |
1 |
La première remarque générale est que si le tableau conduit
n fois pour F à la valeur 1 c'est que F est la somme de n fonctions.
En effet une fonction logique ne peut prendre que deux valeurs 0 ou 1 quels
que soient A, B, C. La table de vérité donne tous les cas possibles
qui ne peuvent être simultanés. Donc F = S dans tous les cas, soit
:
F = 0 + 0 +
f1 + 0 + 0 + 0 + f2 + f3
Cette fonction
est constituée d'une multiplication logique de toutes les variables (ou
de leur complément). On ne s'intéresse qu'aux fonctions conduisant
à F = 1.
Les f1,
f2, f3... sont appelés monomes canoniques. Examinons f1 la table nous
donne
| A = 0 |
soit A = 1 |
|
| B =1 |
|
d'où f1=ABC |
| C = 0 |
soit C = 1 |
|
Le même
cheminement conduit à f2 et f3 d'où F = ABC
+ ABC + ABC on peut ajouter ABC
sans rien changer soit
F = ABC
+ ABC + ABC + ABC
Forme canonique qu'il nous reste éventuellement à simplifier.
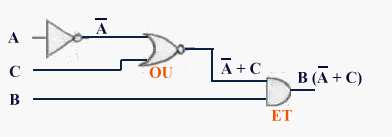
On écrit
immédiatement F = AB ( C +
C) + BC (A +A ) = B (A
+ C)
Ce qu'on peut
retrouver par Karnaugh
D'où
le montage vérifiant la table de vérité
circuit
séquentiel
Soit par exemple
à concevoir un compteur modulo 10
La première
étape consiste à définir le nombre
de bascules, puis à écrire le tableau
des états successifs de chaque bascule, ensuite à partir
de ce tableau on cherchera, en utilisant Karnaugh, les équations
des variables d'entrée de chaque bascule en fonction des sorties,
enfin on établit les connexions assurant
ces états.
Il est important
de noter que lorsqu'on s'intéresse à la synthèse on définit
d'abord les sorties puis les entrées qui vont assurer ces sorties. Pour
ce faire on écrira les tables de vérité des bascules à
l'envers, ainsi pour une bascule JK
| Qt |
Qt+1 |
Jt |
Kt |
|
| 0 |
0 |
0 |
|
maintien à 0 |
| 1 |
0 |
|
1 |
passage à 0 |
| 0 |
1 |
1 |
|
passage à 1 |
| 1 |
1 |
|
0 |
maintien à 1 |
| on avait |
on veut |
pour cela il faut
les entrées |
|
Dans ce tableau
les cases non remplies correspondent à un état indifférent
de l'entrée correspondante.
On va supposer l'emploi de bascules JK. On sait qu'il en faudra 4 puisque 23
< 10 < 24. Ecrivons le tableau des états successifs
en nous fixant comme choix pour les sorties de 0 à 9 les états
binaires normaux sur les sorties Q des bascules ABCD
| |
A |
B |
C |
D |
|
JA |
KA |
JB |
KB |
JC |
KC |
JD |
KD |
| 0 |
0 |
0 |
0 |
0 |
état -->
<-- pour obtenir |
1 |
|
0 |
|
0 |
|
0 |
|
| 1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
|
0 |
|
0 |
|
| 2 |
0 |
1 |
0 |
0 |
|
1 |
|
|
0 |
0 |
|
0 |
|
| 3 |
1 |
1 |
0 |
0 |
|
|
1 |
|
1 |
1 |
|
0 |
|
| 4 |
0 |
0 |
1 |
0 |
|
1 |
|
0 |
|
|
0 |
0 |
|
| 5 |
1 |
0 |
1 |
0 |
|
|
1 |
1 |
|
|
0 |
0 |
|
| 6 |
0 |
1 |
1 |
0 |
|
1 |
|
|
0 |
|
0 |
0 |
|
| 7 |
1 |
1 |
1 |
0 |
|
|
1 |
|
1 |
|
1 |
1 |
|
| 8 |
0 |
0 |
0 |
1 |
|
1 |
|
0 |
|
0 |
|
|
0 |
| 9 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
|
0 |
|
|
1 |
Dans ce tableau
on a, à droite, l'état indispensable
des entrées pour obtenir dans la ligne suivante de gauche
un résultat. Pour les entrées, celles non indiquées sont
indifférentes.
Il nous reste
maintenant à établir l'équation de chacune des variables
d'entrée JA, KA, JB,...en fonction de
A, B, C, D.
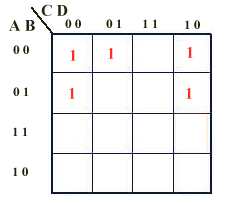
On donne ci-dessus le tableau pour JA. On notera, en reportant les
différents cas rencontrés que, quelles que soient les valeurs
de A, B, C, ou D, JA vaut 1 ou est indifférent (cases non
remplies ci-dessus), il est donc évident qu'on peut alors remplir l'ensemble
du tableau de 1, ce qui revient à dire qu'on prendra JA =
1.
La même
remarque vaut pour KA.
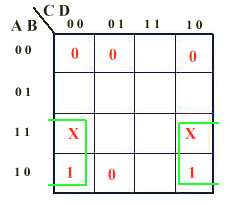tableau
pour JB
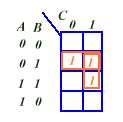
Les cases
marquées d'une croix peuvent prendre une valeur indifférente (de
même que celles non remplies : ça ne change rien au résultat).
On peut donc y placer des 1 et mettre des 0 ailleurs. Cela permet d'identifier
la zone encadrée de vert comme élément de simplification.
Les zéros imposés (figurés dans le tableau) ne permettent
pas d'autre simplification. Rappelons que les chiffres figurant sur ce diagramme
correspondent aux lettres non surlignées. Ainsi, par exemple,en bas à
droite D vaut 0 et C vaut 1 ce qui implique D
=1 et C = 0.
En conséquence
la fonction simplifiée de JB va s'écrire JB
= AD
En
effet si l'on réussit à juxtaposer deux 1, cela élimine
une variable, si on en juxtapose quatre, cela élimine deux variables
et si l'on en juxtapose huit (mais pas 10 ou 9) il reste une variable.
On
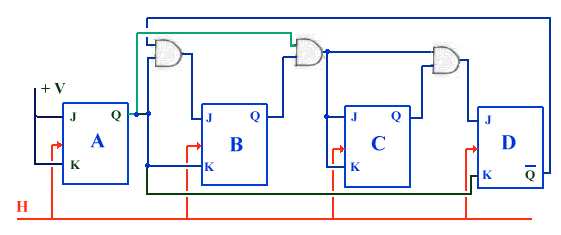
montrera aussi que KA = A, JC = AB, KC = AB,
JD = ABC et KD = A.
Il
en résulte le schéma du compteur.
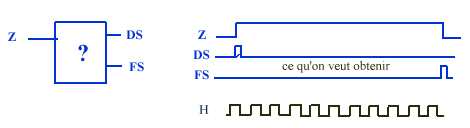
Exemple
3 Synthèse d'un circuit séquentiel
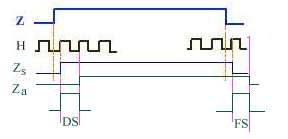
chargé
de détecter le front de montée et le front de descente d'une impulsion
Z de durée notable mais quelconque. On dispose d'une horloge de période
très inférieure à la durée de Z.
DS
doit apparaitre lorsque le signal d'horloge entraine un changement d'état
d'une sortie d'un circuit dont l'entrée est Z. On pense à une
bascule D. Examinons la table de vérité correspondante. On est
amené à préciser une variable Za dite variable interne
qui symbolisera la coïncidence de Z et de l'horloge.
| Za |
Z |
Za+ |
FS |
DS |
|
 |
| 0 |
0 |
0 |
0 |
0 |
Za+ = Z |
| 0 |
1 |
1 |
0 |
1 |
FS = ZaZ |
| 1 |
0 |
0 |
1 |
0 |
DS = ZaZ |
| 1 |
1 |
1 |
0 |
0 |
|
| |
|
Za+ = Za après le front
montant de l'horloge |
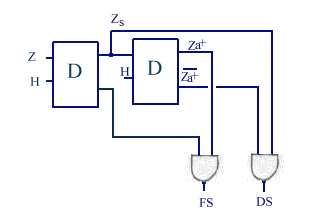
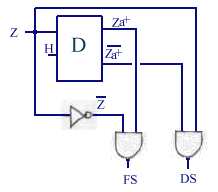
Il faut donc
mémoriser Z : bascule D, inverser Z, faire le ET de Z et
Za ou de Z et Za, ce qui conduirait
au dispositif ci-dessous
Cependant
on s'aperçoit que DS et FS ont des durées variables puisque Z
est asynchrone par rapport à H, ce qui n'est pas satisfaisant. Il convient
donc d'ajouter une synchronisation de Z sur H avant de placer le circuit ci-dessus,
par le biais d'une seconde bascule D.
.
....
Remarque : Il n'y apas de problème de non synchronisme entre variables
internes (Za et Zs ici), mais toujours un problème entre variable externe
(Z) et interne (Za). La solution est obligatoirement de resynchroniser par le
biais d'une bascule ou d'un registre (dans le cas d'un système à
plusieurs bits en parallèle).
Evaluation
de la fréquence maxi d'un dispositif
Soit le système
ci-dessus, à base de JK. Le constructeur indique
| temps de basculement JK |
tpmin - tpmax |
25ns |
| temps de commutation des portes |
tpmin - tpmax |
15ns |
| temps de maintien de la sortie avant le front
d'horloge, plus quelques ns après |
|
20ns |
| marge d'incertitude |
|
50% |
En conséquence, bien que la JK 74LS73 soit donnée pour 30 MHz,
ici avec le temps cumulé des divers étages avec la marge d'incertitude
on obtient 90 ns, soit une fréquence limite pratique de 11 MHz.
Dans le cas d'un circuit ASIC il faudra tenir compte en plus du chemin pour
aller d'un point à l'autre qui selon les lignes utilisées sera
plus ou moins rapide. Un transistor bidirectionnel c'est 6 ns, de même
pour un buffer et un circuit dont l'élément basique est prévu
pour plus de 100 MHz fonctionnera finalement tout juste à 10 MHz!
Exemple
de dispositif à problème
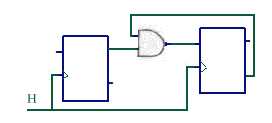
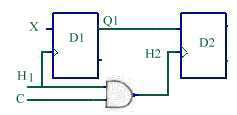
Ce montage
enregistre X dans D1 à chaque impulsion d'horloge et transfère
D1 dans D2 avec la même horloge si C = 1. Or l'horloge H2 est décalée
par rapport à H1 du retard de la porte ET, tandis que la sortie Q1 l'est
du retard de la bascule D1.
Si D1 a un
retard équivalent à la porte ET, le temps de maintien avant l'horloge
ne sera pas respecté,
Si le retard de D1 est supérieur a celui de ET c'est encore pire car
on recopie l'information précédente.
En conséquence il faudra choisir un montage différent dans lequel
:
- l'horloge est appliquée
simultanément sur les deux bascules
- la validation de la recopie
s'effectue par un circuit entre les deux bascules (entre Q1 et D2) qui seront
choisies de type différent (front montant pour D1et front descendant
pour D2)
Avant de fermer cette page consultez notre rubrique de 
