Dans ce chapitre nous allons examiner comment effectuer les quatre opérations arithmétiques bien connues de tous dans le système décimal, mais ici il s'agira de la base 2.

---

Demi additionneur binaire

Considérons la table

X	Y	S	R
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

qui nous donne le résultat de la somme de deux digits binaires S ainsi que la retenue R (carry en anglais), et dont on tire les relations suivantes:

S = X.Y + X.Y qui représente la fonction OU exclusif (S = 1 si X ou Y mais pas les deux sont à 1)

R = X.Y

Le circuit réalisant ces fonctions porte le nom de demi-additionneur. Il peut être réalisé selon le schéma ci-dessous.

soit exclusivement avec des circuits NOR

---

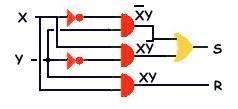
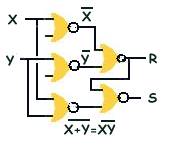
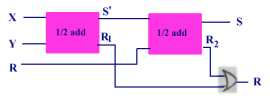
additionneur complet

Pour faire un additionneur complet il faut un circuit qui additionne 2 digits et la retenue de la somme des digits de poids immédiatement inférieur et répondant à la table

X	Y	R-1	S	R
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Cette table correspond aux deux relations

S = R-1 (X.Y + X.Y) + R-1 (X.Y + X.Y)

R = X.Y + R-1 (X.Y + X.Y)

Si l'on pose S' = X.Y +X.Y on voit que S = R-1 S' + R-1 S'

Cette fonction S' est obtenue à l'aide d'un demi-additionneur d'entrée X et Y tandis que S est obtenue avec un demi-additionneur d'entrée S' et R - 1. Enfin R est la somme booléenne des sorties R1 et R2 de ces deux demi-additionneurs

---

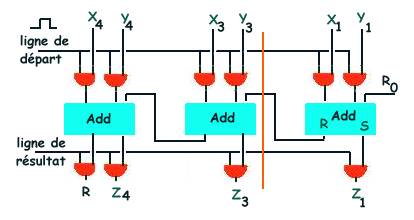
additionneur parallèle

Ce cas est typiquement exploité dans le microprocesseur. Soit 2 nombres de 4 digits X1, X2, X3, X4 et Y1, Y2, Y3, Y4 que l'on désire additionner. Ces nombres sont stockés dans deux registres dont les sorties sont commandées en parallèle. Le dispositif est du type ci-dessous :

Le signal d'horloge appliqué sur la ligne de départ permet la transmission des infos X_n et Y_n simultanément aux 4 additionneurs. Après un décalage dans le temps suffisamment long pour que les retenues générées puissent intervenir dans l'addition le résultat est lu en Z₁, Z₂, Z₃, Z₄ et R après le signal d'horloge sur la ligne résultat. Ce résultat est enregistré dans un nouveau registre.

---

additionneur BCD

Il s'agit typiquement du cas de la calculette. Soit à vouloir effectuer une addition de nombres avec des chiffres décimaux codés en binaire

6 +7	0110 0111
total 13	1101	= S correct en binaire pur mais pas en DCB
R=1 et S=3		avec R=0

En effet en Décimal Codé Binaire on ne peut avec 4 digits dépasser le chiffre 9 soit 1001. Le résultat qui serait correct en DCB doit donc faire intervenir une retenue dès qu'on dépasse 1001 (c'est à dire 10 en décimal). Or avec 4 digits 1111 = 15, il suffit alors de procéder à un décalage de "6", c'est à dire ajouter 0110 pour obtenir le bon résultat

1101 + 0110
1	0011
R=1	, S=3

Cela implique un circuit capable d'ajouter de lui même 0110 si la somme obtenue est incorrecte.
Le circuit devra donc réaliser la fonction logique K = R₄ + S₄ (S₂ + S₃), ce qui peut être obtenu ainsi :

En effet

si l'on fait S₂ + S₃ on obtient:1 dans tous les cas où la somme est > 9 mais aussi certains cas < 9
si l'on fait S₄.(S₂ +S₃) on obtient 1 dans tous les cas > 9 et < 16
et enfin R₄+ S₄ (S₂ + S₃) vaut 1 dans tous les cas > 9.

Cette fonction K sera réalisée avec des NAND et affectera l'étage suivant en parallèle (puisqu'il faut ajouter 0110) sur les entrées X₂ et X₃.

---

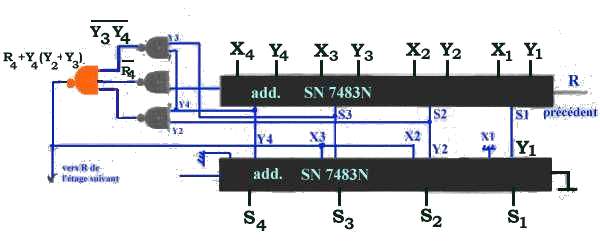
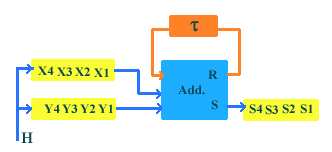
additionneur série

Si les nombres à ajouter sont contenus dans des registres à sortie série. Le circuit d'addition sera :

En H on entre les impulsions qui provoquent le décalage. Le reste est entré dans l'additionneur par une cellule à retard t telle que t soit l'intervalle entre 2 impulsions de décalage. Notons que le registre de sortie peut être le registre X puisq'une fois que X₁ est entré dans l'additionneur la case X₄ est libre et ainsi de suite.

---

soustraction binaire

Plusieurs techniques peuvent être utilisées : Tout d'abord on a l'habitude de représenter un nombre négatif par le positif correspondant précédé du signe moins. La table de soustraction est la suivante

X	- Y	= S	R
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

dont on pourra déduire un opérateur de soustraction. On peut cependant imaginer une autre procédure, dite du complément à 2.

En effet A - B = A - B + 2^N = A + [ 2^N - B ]

So A et B sont codés sur N digits , c'est à dire si notre registre ne dispose que de N digits le 1 de 2^N est électron ignoré et l'on peut écrire ce qui précède.

Souvent dans un ordinateur les nombres sont signés, c'est à dire qu'il y a un digit supplémentaire dit bit de signe qui est à zéro pour un nombre positif et à 1 pour un nombre négatif. En conséquence avant d'effectuer une opération arithmétique les nombres négatifs seront convertis en leur complément à 2 et la soustraction devient alors une addition.

EX 5 -8

8 =1000 le complément à 2 est

10000

- 1000

= 1000

5 = 0101 la soustraction devient l'addition

0	0101
1	1000
1	1101

Pour obtenir le signe du résultat on additionne l'éventuelle retenue de l'addition codée avec les bits de signe et on néglige la retenue de cette dernière addition. On prend alors le complément à 2 du résultat soit dans notre exemple

10000

- 1101

0011

et le résultat final est donc 1 . 0011 (soit - 3)

EX 7 - 2

7 = 0111, 2 = 10 soit en complément à 2 : 1000 - 10 =1110 d'où l'addition codée

1	<-- retenue de l'addition
0	0111
1	1110
10	0101	<-- soit plus cinq
le 1 est ignoré, le 0 est le bit de signe

Si le résultat est positif il n'y a pas besoin de refaire un complément à 2 pour obtenir le résultat final.

On va en déduire la conception du soustracteur

---

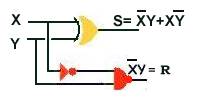
semi-soustracteur

Il répond à la table X -Y = S

X	Y	S	R
0	0	0	0
1	0	1	0
0	1	1	1
1	1	0	0

soit S = X ou exclusif Y et R = X.Y

Si maintenant on tient compte en plus de la retenue provenant de la soustraction du bit de poids plus faible on combinera deux semi-soustracteurs ainsi

---

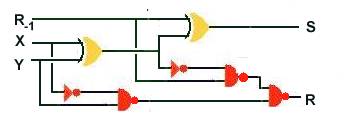
additionneur - soustracteur de nombres signés codés en complément à 2

Au lieu de faire X - Y on va effectuer X + Y*. Le synoptique du principe est le suivant

La porte ET du haut transmet S si R = 0 sinon elle transmet 0, à la sortie du second circuit de complémentation à 2 on obtient S si R = 1. La bascule D est destinée à afficher le signe du résultat : le plus est lié à la sortie Q. X et Y sont évidemment stockés dans des registres.

---

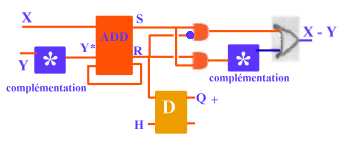
autre procédure

A - B on fait B' complément logique de B ex B = 1011 soit B' = 0100 notons que si l'on fait la somme de B + B' on obtient 1111 soit très précisément 2^N - 1, donc B = (2^N-1) - B'

Il en résulte que A - B = A - (2^N-1) + B' = A + B' + 1 - 2^N on ignore le 2^N puisque son 1 dépasse la capacité de l'additionneur et la soustraction devient une simple addition (le 1 est considéré comme une retenue).

---

multiplication binaire

La multiplication consiste à faire une suite d'additions avec le multiplicande décalé vers la gauche. Cette opération est répétée autant de fois qu'il y a d'éléments binaires dans le multiplicateur.

1101	multiplicande
x 1011	multiplicateur
0001101
0011010	décalage 1 pas
1101000	décalage 3 pas
10001111	résultat

Il faut donc pour réaliser une multiplication disposer de la fonction addition, du décalage et du comptage ce qui implique :

1 registre à décalage pour le multiplicande

1 registre à décalage pour le multiplicateur

1 registre pour le résultat

1 additionneur

1 compteur pour le nombre de pas de décalage

---

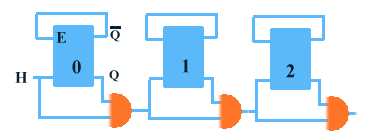
division de fréquence

Sur un compteur binaire tel celui ci-dessous on applique une horloge de fréquence f, à la sortie du premier étage on obtient une fréquence f/2, et au nième étage f/2ⁿ


Une autre façon de réaliser cette division est illustrée sur le schéma suivant qui est préférable dès lors que l'on souhaite vérifier la propagation des données sans être gêné par les temps de hold up ou set up liés au circuit combinatoire connecté à l'horloge.

---

division

EX 85/3 La procédure en décimal est bien connue. On divise 8 par 3, multiplie le reste par 10, l'additionne au chiffre de poids inférieur et on recommence. En binaire l'opération division élémentaire se ramène à une soustraction. D'où la procédure :

1101 à diviser par 0101. On dispose de 3 registres l'un contient le diviseur, l'autre rien au début, le troisième est réservé au dividende

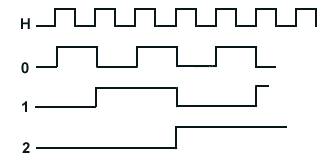24	23	A		20	B
0	0	0	0	0	1	1	0	1

On décale d'un cran vers la gauche et soustrait le diviseur de A, il vient :

				1	1	0	1	0	décalage	: étape 1
-	0	1	0	1						2
1	1	1	0	0						3
+	0	1	0	1						4
	0	0	0	1	1	0	1	0	restauration	5
			1	1	0	1	0	0	décalage	6
-	0	1	0	1						7
1	1	1	1	0						8
+	0	1	0	1						9
0	0	0	1	1	0	1	0	0	restauration	10
0	0	1	1	0	1	0	0			11
-	0	1	0	1						12
0	0	0	0	1	1	0	0		le chiffre à gauche est un 0	13
0	0	0	1	1	0	0	1	0	ajout d'un 1	14
-	0	1	0	1					décalage	15
1	1	1	1	0						16
+	0	1	0	1	0	0	1	0	en vert le quotien 0010 soit 2	17
0	0	0	1	1					en bleu le reste 0011 soit 3	18

ligne 3 : Si le coefficient de 2⁴ (colonne orange) est 1 c'est que le diviseur est supérieur au contenu de A, on met alors un 0 dans la case de droite de B, et on rajoute le diviseur (étape 4 et 5 : restauration), puis on décale de nouveau (étape 6), à l'étape 13 pour la première fois le coefficient de 2⁴ est à 0 après la soustraction, c'est que le contenu de A était supérieur au diviseur, on ne restaure donc plus et on met un 1 dans la case de droite de B, on décale une nouvelle fois et on recommence la soustraction, mais on ne peut aller plus loin. Le quotient est donc dans B et le reste dans A après une dernière restauration.