capteurs
de déplacement inductifs
 Pour suivre un déplacement angulaire
sans aucune limitation du nombre de tours on peut exploiter le phénomène
d'induction. L'idée est relativement simple elle exploite une variation
de champ magnétique dans un bobinage selon le principe figuré
ci-contre.
Pour suivre un déplacement angulaire
sans aucune limitation du nombre de tours on peut exploiter le phénomène
d'induction. L'idée est relativement simple elle exploite une variation
de champ magnétique dans un bobinage selon le principe figuré
ci-contre.
Une roue dentée en matériau ferromagnétique est solidaire
de l'axe en rotation dont on veut connaître la position ou le déplacement.
Un bobinage comportant un noyau aimanté est placé en face et à
chaque fois qu'une dent passe devant l'axe de l'aimant la variation de champ
en résultant induit une impulsion dans le bobinage, impulsion qu'il suffit
alors de compter. La fréquence est évidemment proportionnelle
à la vitesse angulaire. Notons que l'amplitude de l'impulsion peut être
modifiée en raison d'influences électromagnétiques locales,
mais la fréquence n'est pas affectée. Ce capteur de vitesse angulaire
peut aussi être employé dans les mesures de débit de liquide.
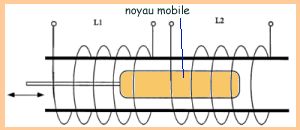 Un déplacement
linéaire peut aussi être mis en évidence par un procédé
Un déplacement
linéaire peut aussi être mis en évidence par un procédé
 inductif. On utilise alors deux bobinages
à l'intérieur desquels un noyau unique est susceptible de se déplacer.
Quand le noyau est en position de référence les deux inductances
sont identiques, dès lors qu'il se déplace d'une quantité
dl l'une des inductances va augmenter de
inductif. On utilise alors deux bobinages
à l'intérieur desquels un noyau unique est susceptible de se déplacer.
Quand le noyau est en position de référence les deux inductances
sont identiques, dès lors qu'il se déplace d'une quantité
dl l'une des inductances va augmenter de  L
et l'autre diminuer symétriquement de
L
et l'autre diminuer symétriquement de  L.
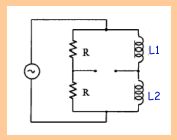
En plaçant l'ensemble dans un montage en pont on va donc récupérer
un signal d'amplitude liée au déplacement du noyau.
L.
En plaçant l'ensemble dans un montage en pont on va donc récupérer
un signal d'amplitude liée au déplacement du noyau.
capteur de déplacement capacitif
Un déplacement linéaire peut aussi être mis en évidence
via un dispositif capacitif. Ainsi sur la figure ci-contre représentant
un 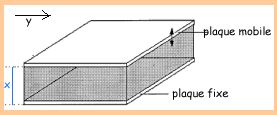 condensateur plan
d'épaisseur x. L'une des armatures, de surface A, est fixe, tandis que
l'autre peut se déplacer en liaison avec le dispositif dont on veut suivre
le mouvement tout en restant parallèle à l'armature fixe.
condensateur plan
d'épaisseur x. L'une des armatures, de surface A, est fixe, tandis que
l'autre peut se déplacer en liaison avec le dispositif dont on veut suivre
le mouvement tout en restant parallèle à l'armature fixe.
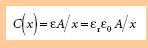 La capacité
varie en fonction inverse de x et peut être insérée très
facilement dans un oscillateur RC dont la fréquence va être fonction
de C donc de x. Notons que la variation relative de capacité est rigoureusement
égale à la variation relative de distance, tandis que la réponse
n'est évidemment pas linéaire puisque la relation entre C et x
est de type hyperbolique. L'intérêt d'un tel principe réside
dans l'absence de contact entre les deux électrodes dont l'une est solidaire
de la pièce en mouvement (c'est à dire peut faire partie intégrante
de cette pièce).
La capacité
varie en fonction inverse de x et peut être insérée très
facilement dans un oscillateur RC dont la fréquence va être fonction
de C donc de x. Notons que la variation relative de capacité est rigoureusement
égale à la variation relative de distance, tandis que la réponse
n'est évidemment pas linéaire puisque la relation entre C et x
est de type hyperbolique. L'intérêt d'un tel principe réside
dans l'absence de contact entre les deux électrodes dont l'une est solidaire
de la pièce en mouvement (c'est à dire peut faire partie intégrante
de cette pièce).
Précisons que ce principe capacitif peut aussi être utilisé
avec x constant mais en faisant varier A (c'est à dire l'aire des électrodes
en regard l'une de l'autre) ce qui peut être obtenu en déplaçant
l'armature mobile non plus selon la direction x mais selon y. Si l'on appelle
ky la réduction de surface en regard on obtient la relation suivante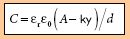 dans
laquelle on voit que la variation de C est linéaire avec y ce qui est
très intéressant évidemment.. C'est d'ailleurs le principe
de "condensateur variable rotatif" qui a été
utilisé pendant de nombreuses années dans les récepteurs
radio pour ajuster l'oscillateur et sélectionner un émetteur précis.
dans
laquelle on voit que la variation de C est linéaire avec y ce qui est
très intéressant évidemment.. C'est d'ailleurs le principe
de "condensateur variable rotatif" qui a été
utilisé pendant de nombreuses années dans les récepteurs
radio pour ajuster l'oscillateur et sélectionner un émetteur précis.
Enfin signalons que l'élément variable peut être le diélectrique.
Ainsi si un tel condensateur de longueur l
plonge partiellement dans un liquide dont la constante diélectrique
 2
sera différente de celle
2
sera différente de celle  1
de l'air, la mesure de la capacité sera un indicateur du niveau y du
liquide.
1
de l'air, la mesure de la capacité sera un indicateur du niveau y du
liquide. 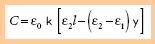 C'est le système
qui a longtemps été le seul utilisé dans les réservoirs
de carburant des automobiles et dans de nombreux dispositifs de stockage de
produits chimiques liquides. Ici encore la relation entre la variation de capacité
et le niveau de liquide y va être linéaire.
C'est le système
qui a longtemps été le seul utilisé dans les réservoirs
de carburant des automobiles et dans de nombreux dispositifs de stockage de
produits chimiques liquides. Ici encore la relation entre la variation de capacité
et le niveau de liquide y va être linéaire.
Souvent dans ce type d'application on choisit une géométrie
circulaire les deux électrodes du condensateur étant
deux cylindres concentriques. Le principe est le même mais les équations
sont sensiblement différentes et on peut, en choisissant judicieusement
les dimensions, obtenir une excellente sensibilité.
capteurs interférométriques
On peut aussi mesurer des distances ou des déplacements avec une très
grande précision en exploitant le principe de l'interféromètre
de Michelson (figure ci-dessus) alimenté par un laser. En effet un faisceau
laser est envoyé sur un miroir semi transparent incliné à
45° ce qui crée deux demi-faisceaux synchrones l'un vers le miroir
fixe (2) l'autre vers un miroir mobile (1). Ces faisceaux réfléchis
par les deux miroirs vont se recombiner au passage du miroir semi transparent
et être dirigés via une lentille concave vers un photodétecteur.
Le trajet des deux faisceaux n'étant pas de la même longueur il
va s'ensuivre un déphasage et donc la création de franges d'interférences
qui vont se déplacer en même temps que le miroir mobile. Un photodétecteur
placé derrière une fente permettra de compter les variations d'intensité
lumineuse liées à ce mouvement amplifié par la lentille
sachant qu'entre deux franges on a un déphasage correspondant à
une demie longueur d'onde. En utilisant un traitement de signal approprié
après le détecteur certains auteurs ont pu atteindre des résolutions
de  /512 ce qui en utilisant
un laser He-Ne émettant à une longueur d'onde de 633nm conduit
à une résolution proche du nanomètre.
/512 ce qui en utilisant
un laser He-Ne émettant à une longueur d'onde de 633nm conduit
à une résolution proche du nanomètre.
Cependant ce principe nécessite une mécanique de qualité
car la moindre vibration du miroir mobile induit des erreurs considérables,
c'est pourquoi on utilise souvent un double interféromètre symétrique
: ainsi une inclinaison parasite du miroir mobile unique produira deux effets
contraires (erreurs) parfaitement symétriques et la demie somme des deux
mesures sera exacte.
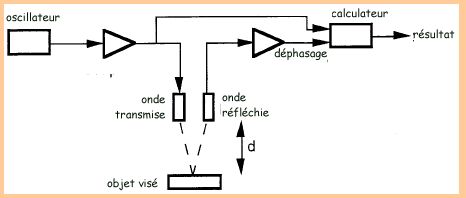
capteurs
à ultrasons à mesure de temps de vol
Lorsqu'une onde ultrasonore traversant un milieu donné rencontre un
autre milieu elle est partiellement réfléchie d'où l'idée
d'exploiter cet écho pour identifier la distance parcourue sachant
que dans le milieu d'épaisseur d l'onde se déplace à
une vitesse c et met un temps t pour effectuer le parcours aller-retour d'où
la relation élémentaire d = ct/2
 En pratique on
peut utiliser directement ce principe lorsque la distance à mesurer
est inférieure à la longueur d'onde de l'onde ultrasonore. Pour
les distances plus grandes on préfère en général
moduler le faisceau émis en fréquence. La dérive de fréquence
du faisceau réfléchi est alors proportionnelle au temps de vol
c'est à dire à la distance. Cette procédure est robuste
vis à vis des perturbations et permet de détecter les multiréflexions.
Cependant il faut se méfier car une distance très grande et
une autre beaucoup plus faible peuvent conduire au même déphasage
apparent.
En pratique on
peut utiliser directement ce principe lorsque la distance à mesurer
est inférieure à la longueur d'onde de l'onde ultrasonore. Pour
les distances plus grandes on préfère en général
moduler le faisceau émis en fréquence. La dérive de fréquence
du faisceau réfléchi est alors proportionnelle au temps de vol
c'est à dire à la distance. Cette procédure est robuste
vis à vis des perturbations et permet de détecter les multiréflexions.
Cependant il faut se méfier car une distance très grande et
une autre beaucoup plus faible peuvent conduire au même déphasage
apparent.
Pour éliminer les bruits provenant de sources industrielles (tels les
systèmes à air comprimé par ex.) on a recours à
des méthodes de corrélation. Les signaux parasites n'étant
pas corrélés avec le signal émis par le système
de mesure peuvent aisément être éliminés.
Ce type de principe peut
être utilisé dans les radars chargés
de piéger les automobilistes trop pressés, mais aussi dans les
systèmes de sécurité chargés de détecter
la présence d'un individu dans une zone
interdite ou au voisinage d'une habitation et pilotant parfois l'allumage
d'un spot d'éclairage. Ainsi dans une agglomération il est possible
de réduire la consommation d'éclairage public dans une voie
piétonne en dotant les lampadaires d'un tel système qui permettra
l'allumage quand un piéton arrive à une certaine distance du
lampadaire et l'extinction quand le piéton sort de ladite zone. On
peut même moduler la puissance de l'éclairage en fonction de
la distance entre le piéton et le lampadaire ce qui est d'autant plus
aisé lorsque ce dernier est équipé de diodes led beaucoup
plus résistantes sur la durée à ce type de comportement
qu'une ampoule à incandescence.
bibliographie
Bourns, Inc., Electronic Components RC4 Solutions Guide, 1995, 304.
G. Lindstedt, Borrowing the bat’s ear for automation. Ultrasonic measurements
in an industrial environment, Dept. of Industrial electrical engineering
and automation, Lund Institute of Technology, 1996.
J. Fraden, AIP Handbook of Modern Sensors, Physics, Design and Applications,
New York: American Institute of Physics, 1993.
S. R. Ruocco, Robot Sensors and Transducers, New York: John Wiley &
Sons, 1987.
J. P. Bentley, Principles of Measurement Systems, 2nd ed., United Kingdom:
Longman Scientific and Technical, 1988.


 Pour suivre un déplacement angulaire
sans aucune limitation du nombre de tours on peut exploiter le phénomène
d'induction. L'idée est relativement simple elle exploite une variation
de champ magnétique dans un bobinage selon le principe figuré
ci-contre.
Pour suivre un déplacement angulaire
sans aucune limitation du nombre de tours on peut exploiter le phénomène
d'induction. L'idée est relativement simple elle exploite une variation
de champ magnétique dans un bobinage selon le principe figuré
ci-contre.  Un déplacement
linéaire peut aussi être mis en évidence par un procédé
Un déplacement
linéaire peut aussi être mis en évidence par un procédé
 inductif. On utilise alors deux bobinages
à l'intérieur desquels un noyau unique est susceptible de se déplacer.
Quand le noyau est en position de référence les deux inductances
sont identiques, dès lors qu'il se déplace d'une quantité
dl l'une des inductances va augmenter de
inductif. On utilise alors deux bobinages
à l'intérieur desquels un noyau unique est susceptible de se déplacer.
Quand le noyau est en position de référence les deux inductances
sont identiques, dès lors qu'il se déplace d'une quantité
dl l'une des inductances va augmenter de  L
et l'autre diminuer symétriquement de
L
et l'autre diminuer symétriquement de  L.
En plaçant l'ensemble dans un montage en pont on va donc récupérer
un signal d'amplitude liée au déplacement du noyau.
L.
En plaçant l'ensemble dans un montage en pont on va donc récupérer
un signal d'amplitude liée au déplacement du noyau. condensateur plan
d'épaisseur x. L'une des armatures, de surface A, est fixe, tandis que
l'autre peut se déplacer en liaison avec le dispositif dont on veut suivre
le mouvement tout en restant parallèle à l'armature fixe.
condensateur plan
d'épaisseur x. L'une des armatures, de surface A, est fixe, tandis que
l'autre peut se déplacer en liaison avec le dispositif dont on veut suivre
le mouvement tout en restant parallèle à l'armature fixe. 2
sera différente de celle
2
sera différente de celle  1
de l'air, la mesure de la capacité sera un indicateur du niveau y du
liquide.
1
de l'air, la mesure de la capacité sera un indicateur du niveau y du
liquide. 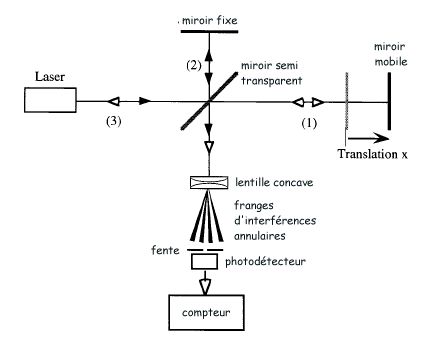
 /512 ce qui en utilisant
un laser He-Ne émettant à une longueur d'onde de 633nm conduit
à une résolution proche du nanomètre.
/512 ce qui en utilisant
un laser He-Ne émettant à une longueur d'onde de 633nm conduit
à une résolution proche du nanomètre. En pratique on
peut utiliser directement ce principe lorsque la distance à mesurer
est inférieure à la longueur d'onde de l'onde ultrasonore. Pour
les distances plus grandes on préfère en général
moduler le faisceau émis en fréquence. La dérive de fréquence
du faisceau réfléchi est alors proportionnelle au temps de vol
c'est à dire à la distance. Cette procédure est robuste
vis à vis des perturbations et permet de détecter les multiréflexions.
Cependant il faut se méfier car une distance très grande et
une autre beaucoup plus faible peuvent conduire au même déphasage
apparent.
En pratique on
peut utiliser directement ce principe lorsque la distance à mesurer
est inférieure à la longueur d'onde de l'onde ultrasonore. Pour
les distances plus grandes on préfère en général
moduler le faisceau émis en fréquence. La dérive de fréquence
du faisceau réfléchi est alors proportionnelle au temps de vol
c'est à dire à la distance. Cette procédure est robuste
vis à vis des perturbations et permet de détecter les multiréflexions.
Cependant il faut se méfier car une distance très grande et
une autre beaucoup plus faible peuvent conduire au même déphasage
apparent.