troisième partie (3/4) : à
perte de charge provoquée
| |
quelques
rappels |
| |
le
plus simple |
| |
le
plus précis |
| |
pour
les grandes turbulences |
| |
capteur
plutôt manuel |
 |
 |
 |
 |
une collection d'icônes
pour visiter tout le site |
Loi
de Bernouilli
Mesurer le débit d'un fluide peut aussi s'effectuer par le biais de capteurs
de pression. L'idée la plus simple consiste à mesurer la pression
en deux points suffisamment distants d'une canalisation et en tenant compte
de la perte de charge. On pourra en déduire par le calcul le débit.
Ce procédé présente l'inconvénient si l'on désire
une bonne résolution et une bonne sensibilité d'imposer une distance
importante entre les deux capteurs, on a donc imaginé de générer
localement une perte de charge importante en jouant non sur la distance mais
sur la géométrie de la canalisation ce qui permettra alors de
faire une mesure de pression différentielle en un seul point quasiment.
On va donc pour cela exploiter la loi de Bernouilli
qui exprime la relation entre débit et perte de charge lors d'un changement
de section de la canalisation.
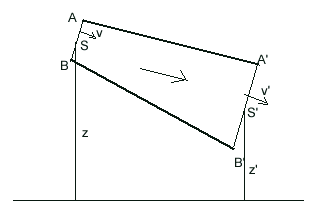
Supposons un tube de courant dont la section est représentée par
la figure ci-dessus dans lequel circule un fluide incompressible et supposé
parfait. Dans ce cas le travail des forces intérieures est nul car il
n'y a ni variation d'énergie potentielle, ni transformation de travail
en chaleur par des frottements internes. De même les forces de contact
qui s'exercent sur les parois du tube leur sont normales et ne fournissent aucun
travail. Les travaux des forces qui agissent sur la masse M de fluide entre
les deux sections droites S et S' du tube en AB et A'B' se réduisent
donc aux travaux des forces de pression p et p' appliquées à ces
mêmes sections et aux travaux des forces de pesanteur. Les premiers peuvent
s'exprimer par pS v dt et p'S'
v' dt, d'une part, et (z-z')g dm, d'autre
part, correspondant au passage de la masse dm de z à z'. Notons que vdt
est la distance dont s'est déplacée la section S en un temps dt
ce qui correspond à l'élément de masse dm, bien évidemment
pendant le même temps dt une même quantité de fluide dm s'est
déplacée à l'autre extrémité du tube puisque
nous avons admis qu'il était incompressible.
On considère donc la masse dm animée d'une vitesse v en z et v'
en z', si l'on appelle  la
masse spécifique du fluide on conçoit aisément que dm
=
la
masse spécifique du fluide on conçoit aisément que dm
=  S vdt=
S vdt= S'
v'dt
S'
v'dt
La variation d'énergie cinétique entre z et z' (théorème
des forces vives) s'exprime par 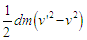 entre t et t+dt ce qui en remplaçant dm par ses expressions ci-dessus
conduit à
entre t et t+dt ce qui en remplaçant dm par ses expressions ci-dessus
conduit à 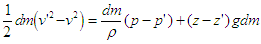 ce qu'on écrit généralement sous la forme
ce qu'on écrit généralement sous la forme 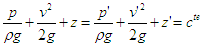 théorème dit de Bernouilli qui exprime
la relation entre vitesse et pression ou variation de vitesse et perte de charge
lors d'un changement de section. En pratique cela fonctionne correctement pour
les écoulements turbulents. Ici encore on va remonter au débit
à partir de la vitesse elle-même identifiée à partir
de la mesure de pression.
théorème dit de Bernouilli qui exprime
la relation entre vitesse et pression ou variation de vitesse et perte de charge
lors d'un changement de section. En pratique cela fonctionne correctement pour
les écoulements turbulents. Ici encore on va remonter au débit
à partir de la vitesse elle-même identifiée à partir
de la mesure de pression.
 Notons que fréquemment
la conduite sera horizontale, ainsi dans le cas typique du tube de Venturi les
termes z et z' seront égaux et s'éliminerons d'office.
Notons que fréquemment
la conduite sera horizontale, ainsi dans le cas typique du tube de Venturi les
termes z et z' seront égaux et s'éliminerons d'office.
Plusieurs déclinaisons de ce principe sont exploitées en pratique.
Actuellement tous les systèmes commercialisés respectent la norme
ISO 5167-1 qui définit tous les paramètres, les dimensionnements
de canalisation et les calculs associés ainsi que les incertitudes, norme
que l'on peut évidemment se procurer à l'AFNOR.
utilisation d'un diaphragme
On place dans la canalisation un disque percé d'un trou de diamètre
inférieur à celui de la canalisation qui crée une pression
différentielle de part et d'autre du diaphragme. C'est le dispositif
le plus simple.
Dans cette relation  est la
densité du fluide en amont du diaphragme, d le diamètre du diaphragme,
est la
densité du fluide en amont du diaphragme, d le diamètre du diaphragme,
 =d/D le rapport des diamètres,
C est le coefficient empirique d'écoulement et
=d/D le rapport des diamètres,
C est le coefficient empirique d'écoulement et  le facteur d'expansion. Les coefficients C et
le facteur d'expansion. Les coefficients C et  sont donnés, pour une géométrie donnée, dans la
norme ISO 5167-1 ou API 2530 (aux USA).
sont donnés, pour une géométrie donnée, dans la
norme ISO 5167-1 ou API 2530 (aux USA).
L'intérêt fondamental de ce principe est qu'il est peu coûteux,
ne possède aucune pièce d'usure et qu'il ne nécessite
aucun étalonnage s'il est réalisé en respectant la norme.
Il est utillisable aussi bien pour les liquides que les gaz et vapeurs.
Notons qu'il n'est pas recommandé pour les fluides chargés en
particules solides qui peuvent s'accumuler auprès du diaphragme et
finir par réduire l'ouverture et donc fausser la mesure.
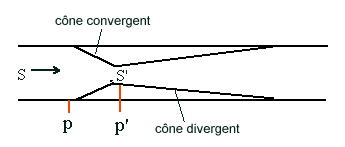
venturi
En faisant se succéder un cône convergent et un cône divergent
on obtient le même effet, mais avec moins de risque d'encrassement.
Noter que le cône convergent est beaucoup plus court que le divergent.
Le débit est directement proportionnel à la racine carrée
de la différence des pressions.
 ...
...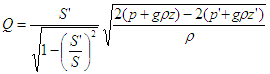
La précision obtenue est supérieure (0.5% à 3% environ
selon le type de fluide)
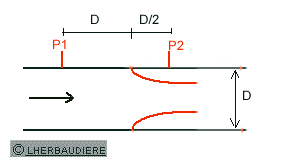
tuyère
C'est une variante du tube de Venturi avec une perte de charge supérieure
On notera la position des prises de pression à une distance égale
au diamètre de la canalisation pour la prise amont et à un demi
diamètre pour la prise aval
rotamètre
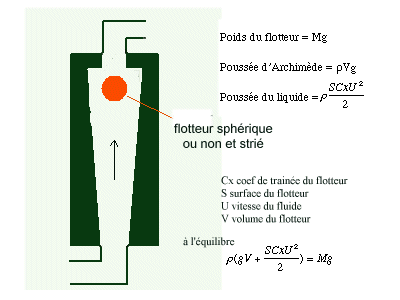
Un autre procédé consiste à intégrer dans une
portion de canalisation en verre, verticale à section croissante de
bas en haut, un flotteur calibré. La position de celui-ci dépendra
de son poids, de la poussée d'Archimède et de celle du liquide
(ou du gaz) en déplacement vers le haut. On repère le plus souvent
la position du flotteur en lisant directement la graduation sur le tube de
verre, mais on peut imaginer des repérages optiques ou magnétiques
automatisés. Lorsque le flotteur n'est pas sphérique il est
généralement strié ce qui va entrainer sa mise en rotation
et améliorer sa stabilité.
 ...
...
Dans le cas où le rotamètre a une géométrie conique
dont le diamètre varie linéairement selon son axe soit D=D0+az
on va pouvoir à partir de la relation à l'équilibre
ci-dessus exprimer la vitesse U au niveau z du flotteur, soit 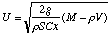 d'où
on tirera évidemment le débit
d'où
on tirera évidemment le débit 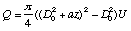 .
Le rotamètre doit être étalonné soigneusement dans
ses conditions réelles de fonctionnement et ne peut tolérer de
pressions élevées (< 20 bars). Sa précision est médiocre
(parfois seulement 10%).
.
Le rotamètre doit être étalonné soigneusement dans
ses conditions réelles de fonctionnement et ne peut tolérer de
pressions élevées (< 20 bars). Sa précision est médiocre
(parfois seulement 10%).

R. A. Furness, Flowmetering: evolution or revolution, Measurement and Control,
27 (8), 15-18, 1994.
International Organization for Standardization, ISO 5167-1, Measurement
of Fluid Flow by Means of Pressure Differential Devices — Part 1 Orifice
plates, nozzles and Venturi tubes inserted in circular cross-section conduits
running full, Geneva, Switzerland, 1991.
M. J. Reader-Harris, J. A. Slattery, and E. P. Spearman, The orifice plate
discharge coefficient equation — further work, Flow. Meas. Instrum.,
6 (2), 101-114, 1995.


 la
masse spécifique du fluide on conçoit aisément que dm
=
la
masse spécifique du fluide on conçoit aisément que dm
=  S vdt=
S vdt= S'
v'dt
S'
v'dt
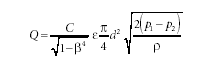
 est la
densité du fluide en amont du diaphragme, d le diamètre du diaphragme,
est la
densité du fluide en amont du diaphragme, d le diamètre du diaphragme,
 =d/D le rapport des diamètres,
C est le coefficient empirique d'écoulement et
=d/D le rapport des diamètres,
C est le coefficient empirique d'écoulement et  le facteur d'expansion. Les coefficients C et
le facteur d'expansion. Les coefficients C et  sont donnés, pour une géométrie donnée, dans la
norme ISO 5167-1 ou API 2530 (aux USA).
sont donnés, pour une géométrie donnée, dans la
norme ISO 5167-1 ou API 2530 (aux USA). ...
...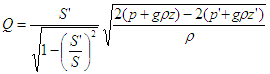
 ...
...
